Se certificar de qunando usar o Matlab para realizar os projetos de controladores mostrados aqui, concentrar os dados num mesmo diretório:
>>pwd
ans =
'/Volumes/Data/Users/fernandopassold/Documents/UPF/Controle_3/2020_1'A planta usada para projeto de diferentes controladores é sempre a mesma:
\( G(s)=\dfrac{1}{(s+1)(s+2)(s+10)} \)
Um sistema de 3a-ordem, do tipo 0, isto é, se não for acrescentada ação integral à função transferência de malha aberta do sistema completo, sempre havera algum erro (ele não poderá ser anulado).
Ingressando com esta planta no Matlab:
>> G=tf( 1, poly( [ -10 -2 -1] ) );
>> zpk(G)
ans =
1
------------------
(s+10) (s+2) (s+1)
Continuous-time zero/pole/gain model.
>>Precisamos determinar agora \(BoG(z)\), e para tanto, necessitamos considerar o período amostragem sendo adotado. Para este estudo de caso e esta planta \(T=0,1\) segundos sempre:
>> T=0.1; % periodo de amostragem;
>> BoG=c2d( G, T);
>> zpk(BoG)
ans =
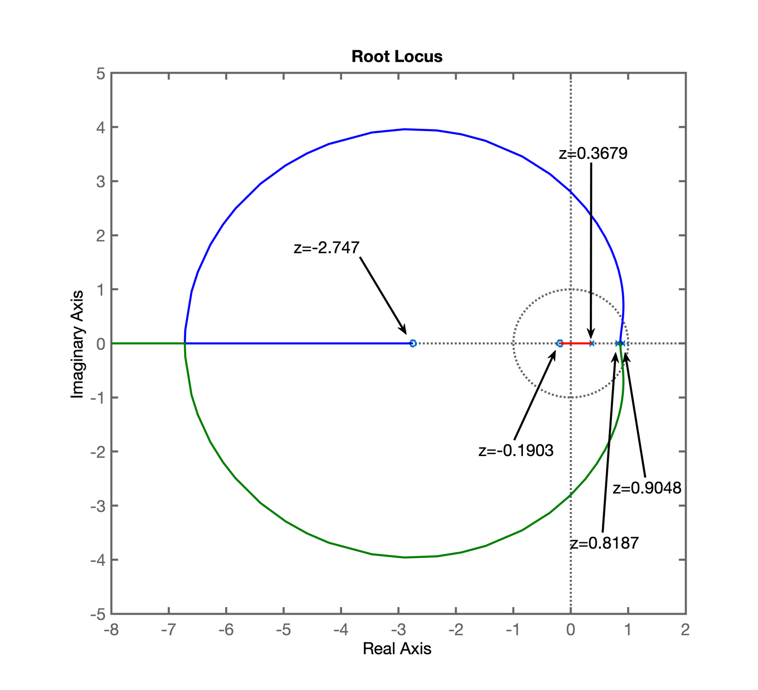
0.00012224 (z+2.747) (z+0.1903)
--------------------------------
(z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
>>Agora podemos iniciar o projeto do Controlador Proporcional.
Neste caso, não acrescentamos nenhum pólo nem zero, apenas fechamos a malha com um ganho. A questão é saber que ganho adotar. Para tanto, fazemos uso da ferramenta Root Locus para entender (interpretando o gráfico), como este sistema se comporta.
>> rlocus(BoG)É gerada uma figura como:

O RL sozinho não serve de muita coisa, para definir o controlador, se faz necessário tomar conhecimente de requisitos de controle para limitar as opções disponíveis.
Neste projeto inicial, vamos considerar que o único requisito de controle que foi passado é limitar o sobressinal a no máximo 10%.
Então podemos usar a teoria de respostas de sistemas lineares de 2a-ordem em MF para o caso sub-amortecido e assim, para este valor de \(\%OS\) temos como inferior o valor de \(\zeta\) (fator de amortecimento):
>> OS=10;
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
0.5912
>>Aproveitamos que o valor de \(\zeta\) foi encontrado para sobrepor no RL anteiormente traçado, a linha guia para este valor de \(\zeta\):
>> hold on;
>> zgrid(zeta,0);E aproveitamos para usando a função rlocfind(.) descobrir que valor de ganho deve ser usado para fazer o RL atingir o ponto onde o \(\zeta\) coincide com o valor buscado:
>> [K, polos_MF ]=rlocfind(BoG)
Select a point in the graphics window
selected_point =
0.8710 + 0.1513i
K =
27.4831
polos_MF =
0.8707 + 0.1514i
0.8707 - 0.1514i
0.3467 + 0.0000i
>>Ver figura à seguir:
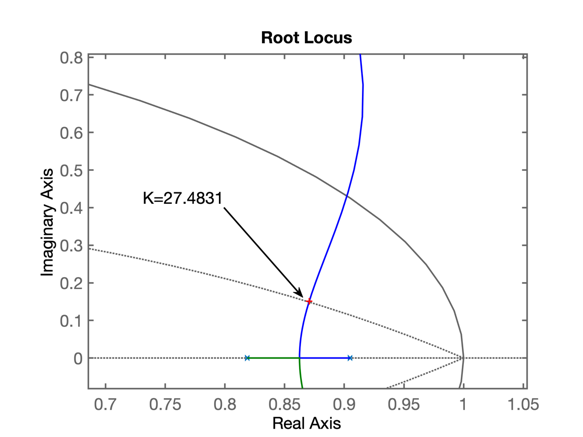
E agora fechamos a malha com este valor de ganho, \(K=27.4831\):
>> ftmf=feedback(K*BoG, 1);
>> figure; step(ftmf)O que rende o gráfico:
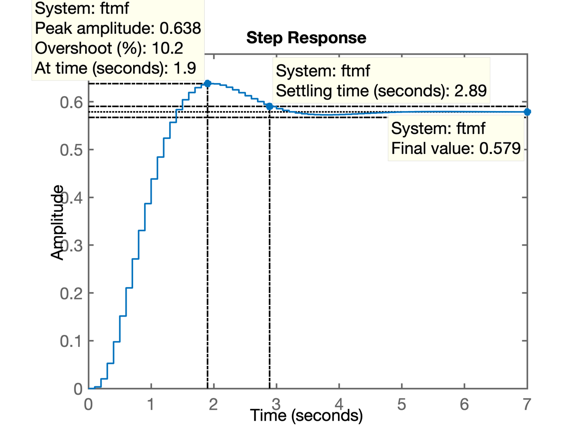
Notamos que este valor de ganho ultrapassou um pouco o sobressinal especifiaco, mas o que deveria chamar mais a atenção é o valor de regime permanente alançado pelo sitema em malha-fechada, ou simplesmente \(y(\infty)\):
>> dcgain( ftmf )
ans =
0.5788Percebe-se que está algo distante de 1,0 que a amplitudade do degrau utilizado.
Podemos calcular o erro em regime permanente:
>> erro=(1-dcgain(ftmf))/1*100
erro =
42.1202E confirmamos que este erro é elevado (42,12%).
Existe o comando stepinfo(.) do Matlab para descobrir algumas características de respostas de um sistema, aprocximadas para um sistema de 1a-ordem (esta função separa os 2 pólos mais dominantes; neste caso, os 2 pólos mas próximos do círculo unitário e realiza os cálculos das caractetíricas levando em conta apenas estes 2 pólos, como que aproximando a resposta do sitema para um de 2a-ordem):
>> stepinfo(ftmf)
RiseTime: 0.8000
SettlingTime: 2.9000
SettlingMin: 0.5238
SettlingMax: 0.6379
Overshoot: 10.2164
Undershoot: 0
Peak: 0.6379
PeakTime: 1.9000Uma forma de baixar o erro (que não poderá ser anulado porque falta uma ação integral nesta FTMA) é aumentar o ganho, mas respeitando o valor máximo que pode ser adotado. Neste caso, \(K_{max}=258\):
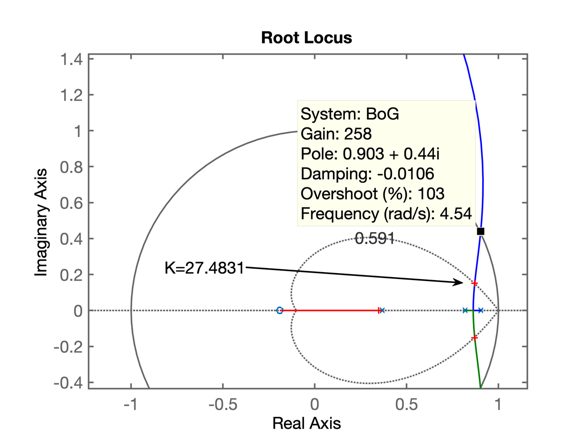
Adotando \(K_2=200\) vamos obter o seguinte resultado:
>> K2=200;
>> ftmf2=feedback(K2*BoG, 1);
>> figure; step(ftmf2)Com o seuinte gráfico para a resposta ao degrau:
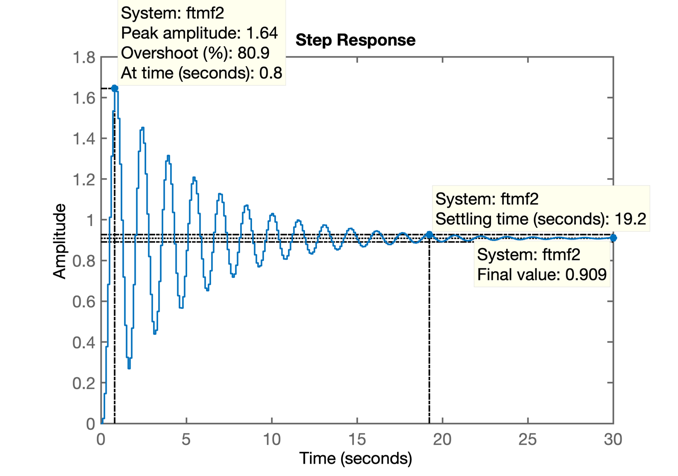
Percebe-se que o erro foi reduzido, mas as custas de um overshoot bastante elevado e maior tempo de assentamento.
Finalizando esta seção de trabalho no Matlab: não esquecer de ingressar os seguintes comandos:
>> save dados
>> diary offFim
Prof. Fernando Passold, em 07/05/2020.