
Photo by Petar Petkovski on Unsplash
5.5) Aplicação do Método de Jury (Determinação de )
Problema/Exemplo:
Seja a planta:
Considere: a) ; b)
Suponha que esta planta será incorporada numa malha-fechada com Controlador Proporcional:

Determine para os 2 casos de períodos de amostragem.
Resolução:
Primeiro deve-se calcular (ver “apostila.pdf”):
; ; .
De posse da ou que é o caso aqui, se determina a :
Aplicando os 3 pré-requisitos referentes ao método de Jury (análise de Estabilidade), temos que:
(1) .
(2) ; Obs: .
(3) ; Obs: .
Resolvendo numericamente usando Matlab:
a)
x
>> T=0.1;>> a=exp(-T)a = 0.9048>> b1=exp(-T)+T-1b1 = 0.0048>> b0=1-exp(-T)-T*exp(-T)b0 = 0.0047>> BoG=tf( [b1 b0], poly([ 1 a ]), T ); % não esquecer de informar 3o-parametro: periodo amostragem, senão Matalb supõe que esta 'tf' seja no plano-s>> zpk(BoG) 0.0048374 (z+0.9672) -------------------- (z-1) (z-0.9048) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.>> Outra maneira de determinar :
x
>> % Outra maneira>> G = tf( 1, [1 1 0] );>> zpk(G) 1 ------- s (s+1) Continuous-time zero/pole/gain model.>> BoG = c2d (G, T); % usando função 'c2d' para calcular BoG(z)>> zpk(BoG) 0.0048374 (z+0.9672) -------------------- (z-1) (z-0.9048)Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.>>Aplicando os critérios de Jury sobre esta :
xxxxxxxxxx>> TT = 0.1000>> % Continuando com cálculo de EC(z):>> a2=1;>> % pré-requisito (2):>> K = 2*(1+a)/(b0-b1)K = -2.4024e+04>> % pré-requisito (3):>> K = (1-a)/b0K = 20.3389>> (b0-b1)ans = -1.5858e-04>> Conclusão: com .
b) :
x
>> T=1;>> a=exp(-T)a = 0.3679>> b1 = exp(-T)+T-1b1 = 0.3679>> b0=1-exp(-T)-T*exp(-T)b0 = 0.2642>> BoG=tf( [b1 b0], poly([ 1 a ]) , T); % não esquecer de informar 3o-parametro: periodo amostragem, senão Matalb supõe que esta 'tf' seja no plano-s>> zpk(BoG) 0.36788 (z+0.7183) ------------------ (z-1) (z-0.3679) Sample time: 1 secondsDiscrete-time zero/pole/gain model.>> Aplicando os critérios de Jury sobre esta :
x
>> % pré-requisito (2):>> K = 2*(1+a)/(b0-b1)K = -26.3972>> % pré-requisito (3):>> K = (1-a)/b0K = 2.3922Conclusão: com .
Comparando resultados:
| a) | b) |
|---|---|
rlocus():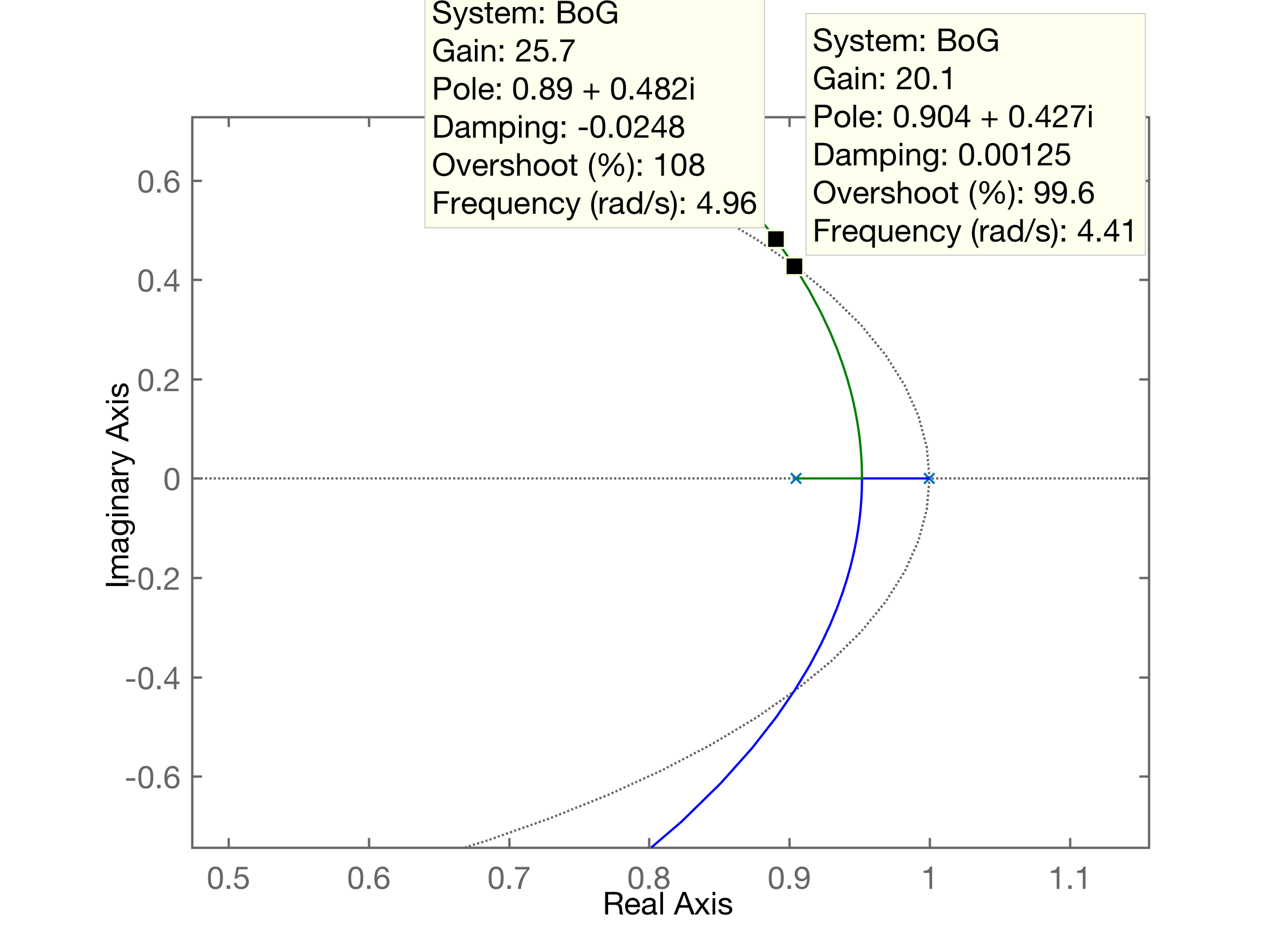 | locus():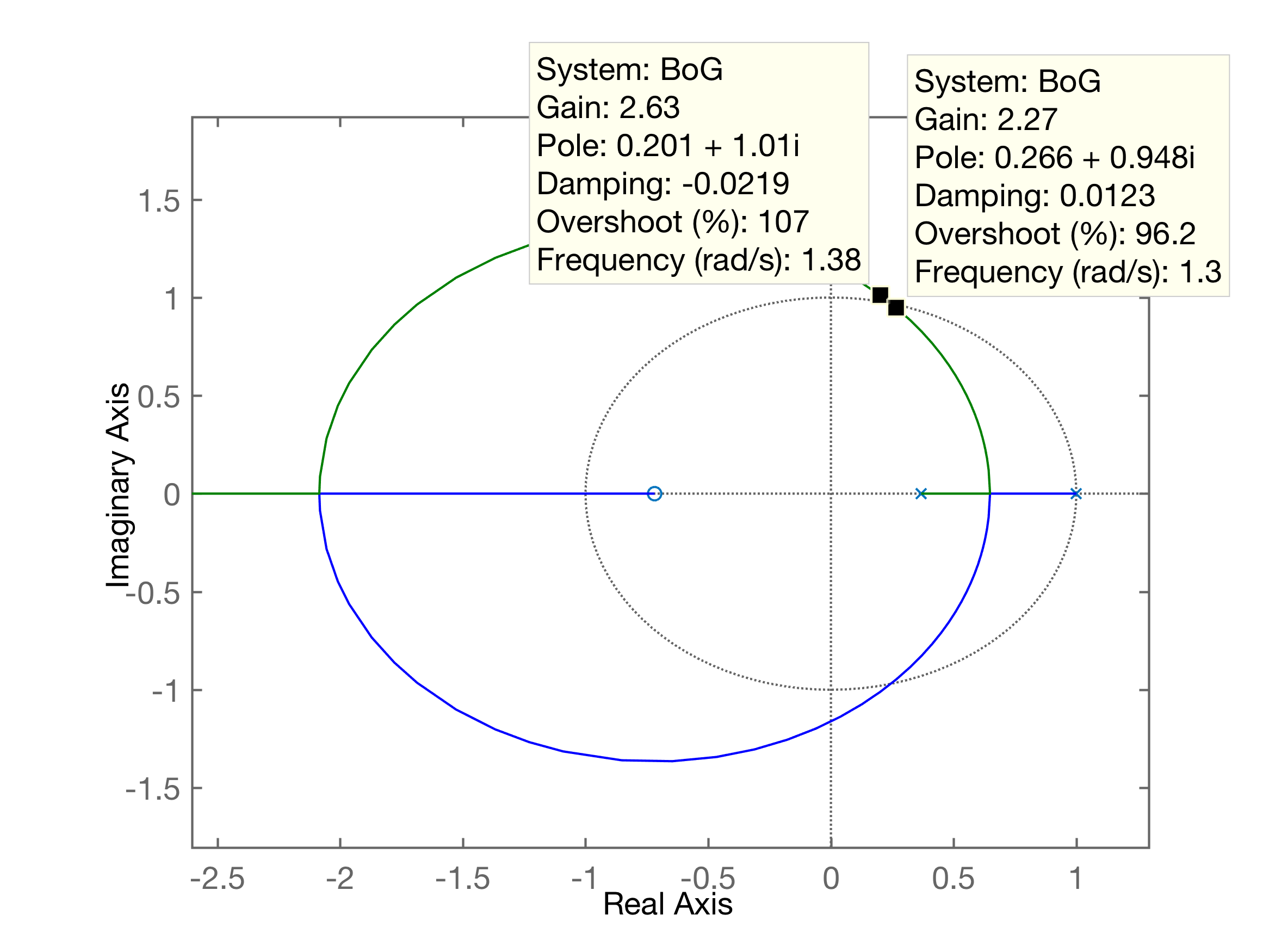 |
Conclusão final:
Nota-se que a medida que aumenta o período de amostragem T, se é obrigado a abaixar o ganho K do controlador, para manter a estabilidade do sistema, ou:
Fim.
Fernando Passold, 14.04.2021