Aula de 28/10/2020.
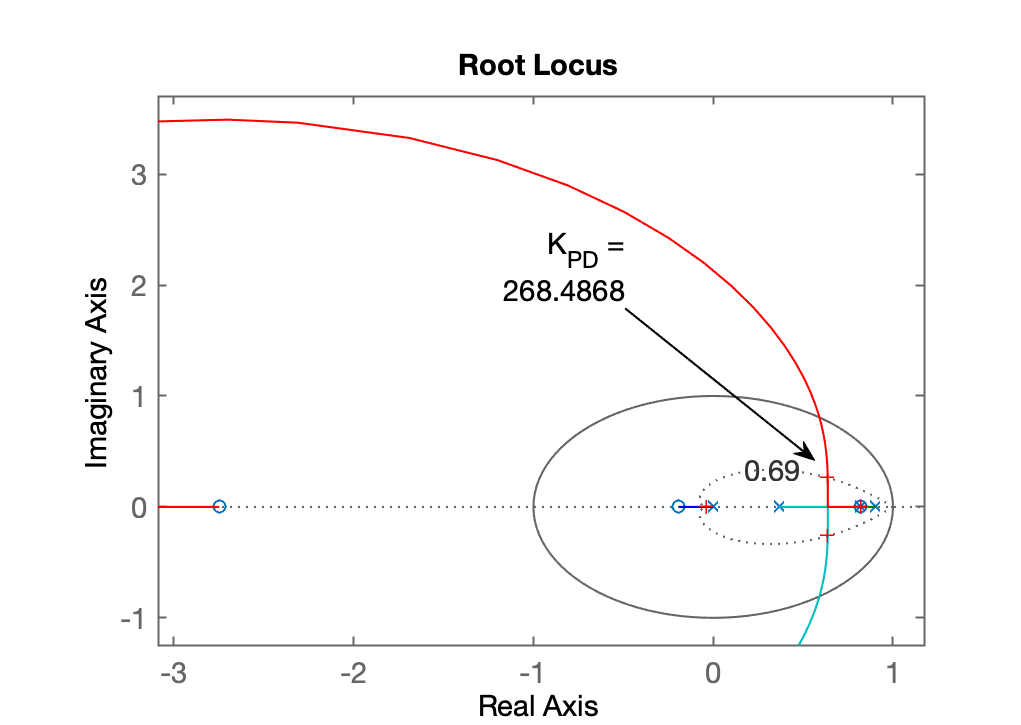
Conforme discussão prévia em sala, analisando o plano-s com os pólos e zeros da planta + o pólo na origem do PD, faltava definir uma posição para o zero do PD. Pela análise do Root Locus, percebe-se que o PD deve gerar respostas mais rápidas (pólos de MF mais rápidos), se o seu zero estiver localizado entre os 2 pólos mais lentos desta planta: \(0.8187 \le \text{zero}_{\text{PD}} \le 0.9048\).
Retomando seção de trabalho anterior no Matlab:
>> load planta % carrega dados das seções anteriores
>> zpk(BoG) % verificando
ans =
0.00012224 (z+2.747) (z+0.1903)
--------------------------------
(z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
>> pzmap(BoG) % mostrando no plano-z os pólos e zeros de BoG(z)
>> % implementando o PD
>> PD=tf(poly(0.82), poly(0),T);
>> zpk(PD) % confirmando ingresso correto de dados
ans =
(z-0.82)
--------
z
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
>> ftma_PD=PD*BoG;
>> figure; rlocus(ftma_PD)
>> hold on;
>> OS
OS =
5
>> zgrid(zeta,0)
>> [K_PD,poloMF]=rlocfind(ftma_PD)
Select a point in the graphics window
selected_point =
0.6375 + 0.2619i
K_PD =
268.4868
poloMF =
0.8205 + 0.0000i
0.6372 + 0.2619i
0.6372 - 0.2619i
-0.0361 + 0.0000i
% GRáfico do RL para este PD
% Gráfico do RL gerado para este PD:

Fechando a malha:
>> ftmf_PD=feedback(K_PD*ftma_PD, 1);
>> figure; step(ftmf, ftmf_PD)
>> % Gráfico da resposta ao degrau
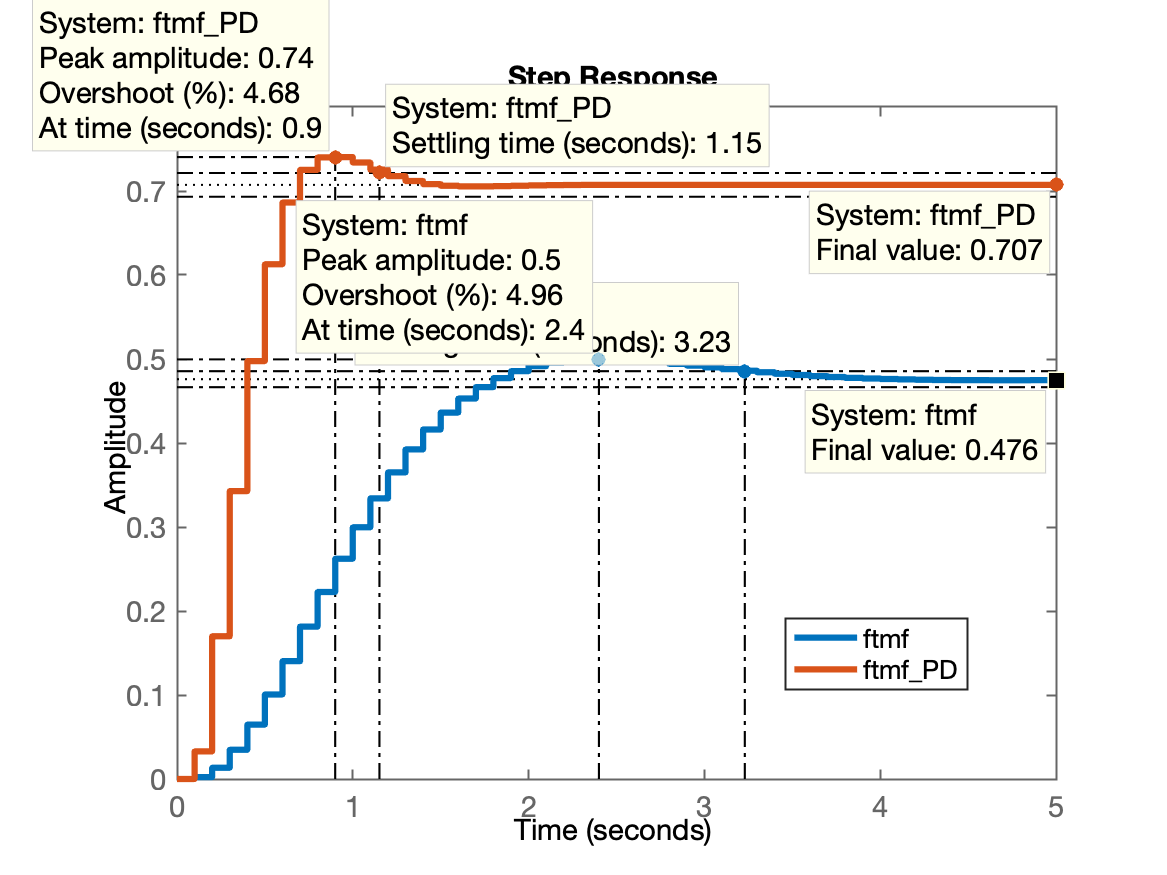
>> % 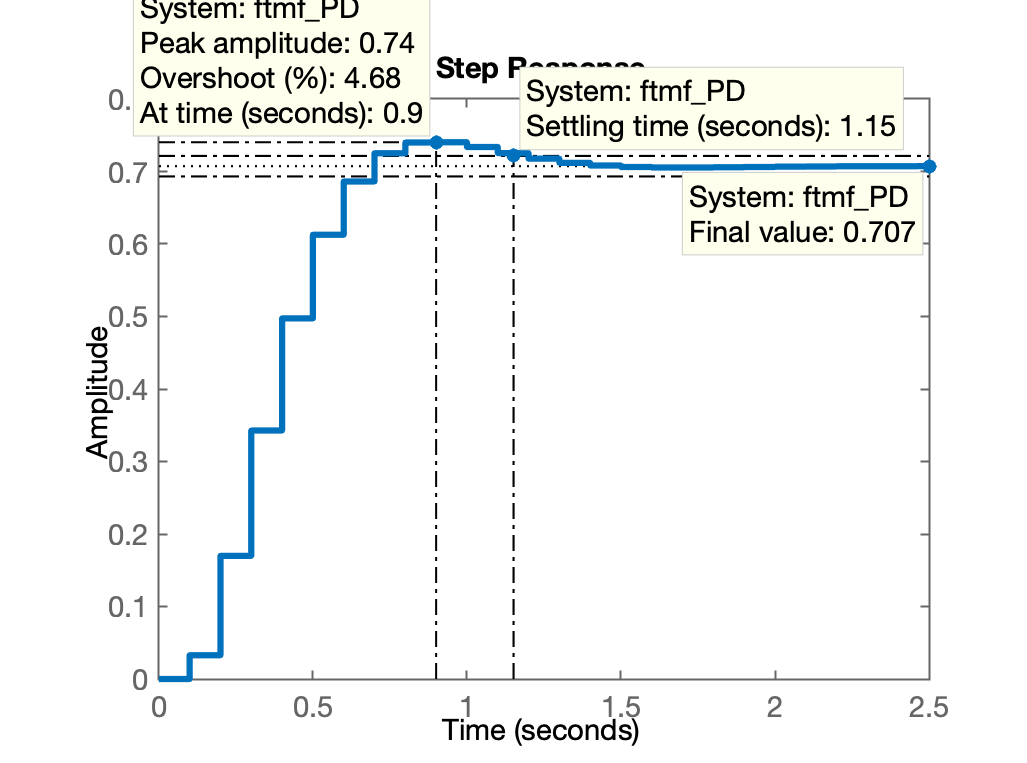Gráfico da resposta ao degrau (comparando com controlador Proporcional):
Alguns dados:
>> stepinfo(ftmf_PD)
RiseTime: 0.4000
SettlingTime: 1.2000
SettlingMin: 0.6862
SettlingMax: 0.7404
Overshoot: 4.6764
Undershoot: 0
Peak: 0.7404
PeakTime: 0.9000
>> dcgain(ftmf_PD)
ans =
0.7073Repare nos erros:
>> erro_PD=(1-dcgain(ftmf_PD))/1*100
>> erro_PD =
29.2707
>>
>> erro_Kp=(1-dcgain(ftmf))/1*100
>> erro_Kp =
52.4061
>> % comparando tempos de assentamento
>> 3.23/1.15
ans =
2.8087Nota-se que o PD acelerou um sistema em 2,8 vezes e reduziu (mas não cancelou) erro em regime permanente, em comparação com controlador Proporcional.
Verificando agora as amplitudes das ações de controle
>> % levantando equações auxiliares para uso de step e gráficos de u[kT']
>> u=K/(1+K*BoG); % cont. Proporcional
>> uPD=K_PD*PD/(1+K_PD*PD*BoG); % PD
>> figure; step(u, uPD)
>> title('Ações de Controle');Gráfico das ações de controle:
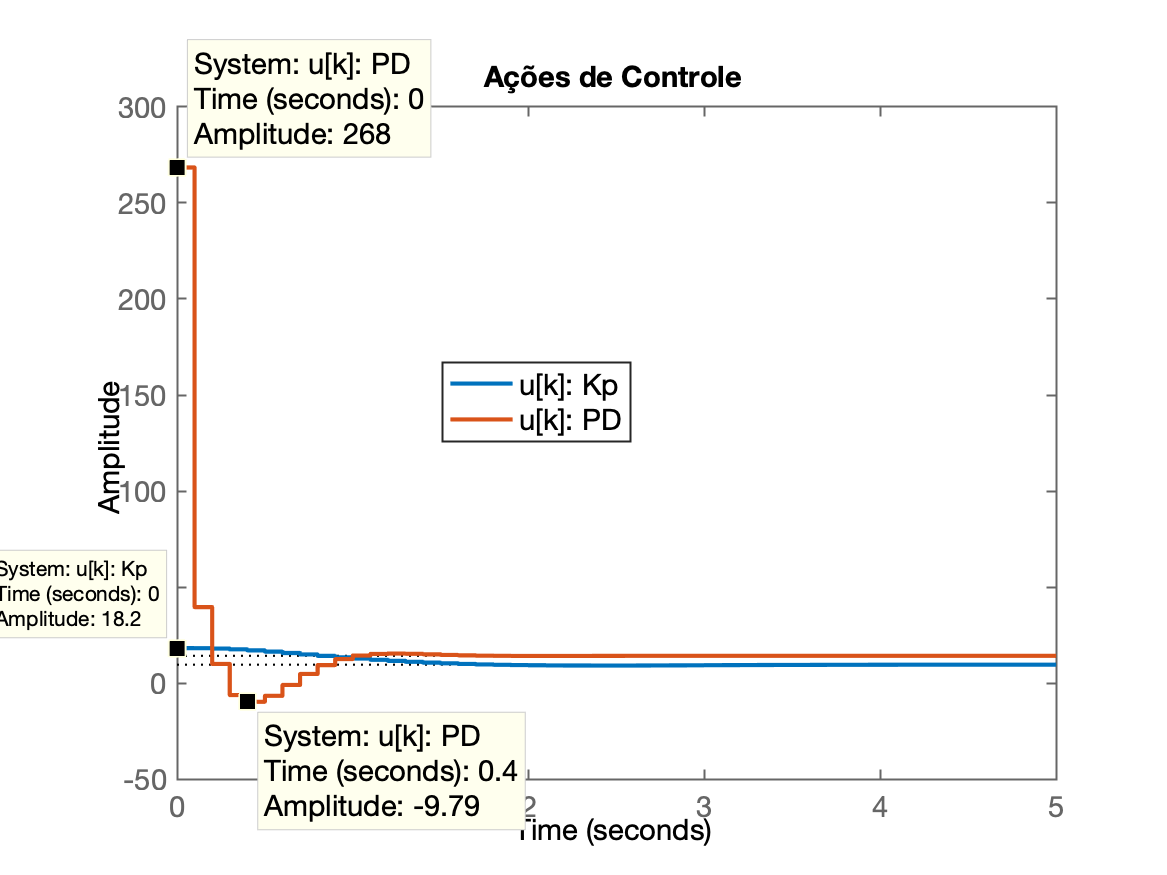
Note as amplitudes iniciais geradas pelos controladores:
>> K_PD
K_PD =
268.4868
>> K
K =
18.1635
>> % relação entre valor inicial de u[kT] gerado pelo PD x Proporcional
>> K_PD/K
ans =
14.7817Mas em compensação o PD reduziu tempo de assentamento pela metade ou menos:
>> 3.23/2
ans =
1.6150Encerrando atvidades desta aula:
>> save planta
>> diary offFernando Passold, em 28/10/2020.