Aula de 14/10/2020
Relembrando a planta usada para estudo de caso:
» zpk(BoG)
ans =
0.00012224 (z+2.747) (z+0.1903)
--------------------------------
(z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.Equação do PI:
\[ C(z)=K_p+\dfrac{K_i}{(z-1)}=\frac{K_p z - K_p + K_i}{(z-1)} \] \[ C(z)=\dfrac{ K_p \left[ z - \left( 1 - \dfrac{K_i}{K_p}\right) \right] }{(z-1)} \]
O problema aqui é definir a posição do zero.
Usando Matlab para levantar o RL de \(BoG(z)\) e parte do controlador PI sem o zero, para avaliar posições para seu zero:
» PI_aux=tf(1 , [1 -1], T); % PI sem o zero!
» zpk(PI_aux) % conferindo expressão do PI_aux sem o zero ainda
ans =
1
-----
(z-1)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
» ftma_aux=PI_aux*BoG;
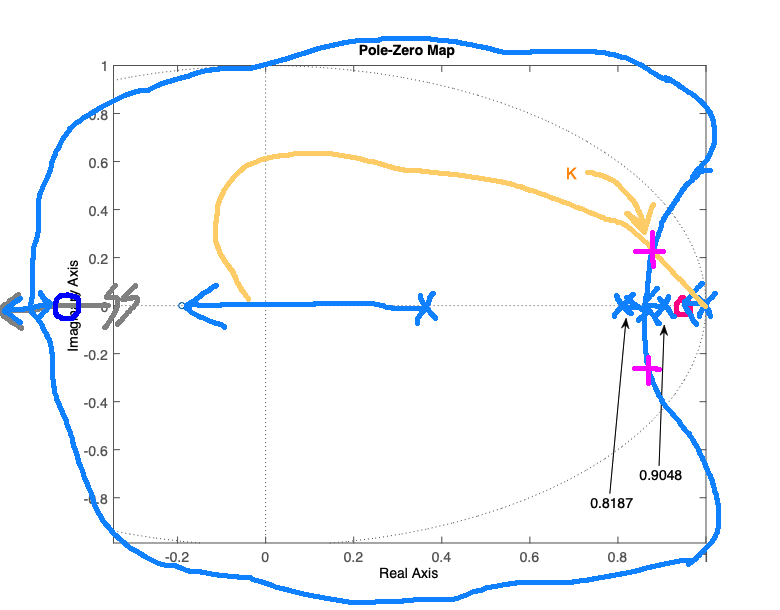
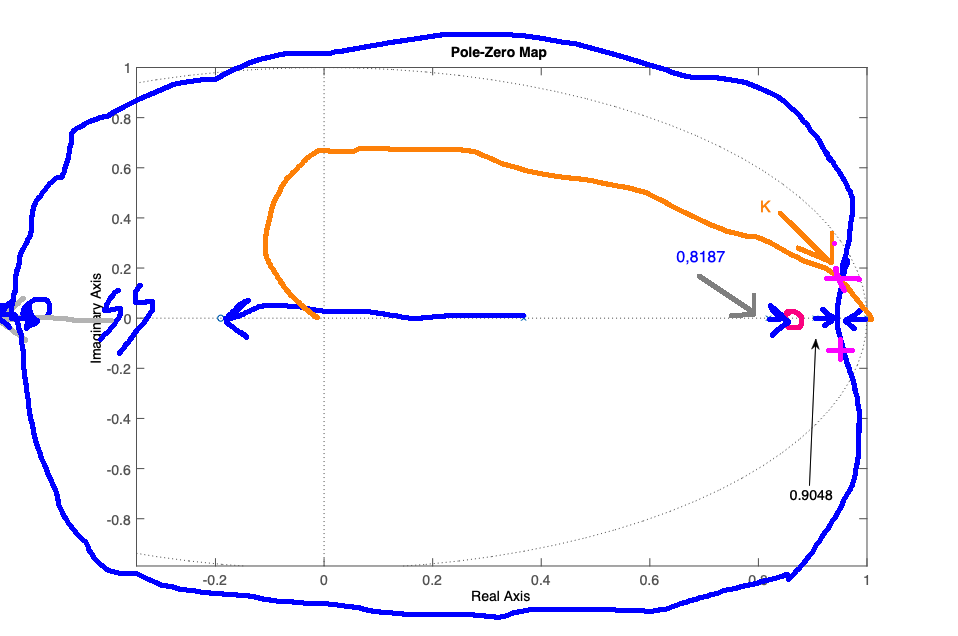
» pzmap(ftma_aux)
» % Lembrando dos pólos e zeros da planta:
» zpk(BoG)
ans =
0.00012224 (z+2.747) (z+0.1903)
--------------------------------
(z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.Raciocínio usando RL como ferramenta de decisão:
Opção 1) Colocar 0,9048 < zero_PI < 1 (integrador) (entre o integrador e o pólo + lento)
Opção 2) Colocar o 0,8187 < zero_PI < 0,9048 (entre os 2 pólos mais lentos da planta)
 |
 |
|---|---|
| Opção 1: | Opção 2: |
| 0,9048 < zero_PI < 1 | 0,8187 < zero_PI < 0,9048 |
Observe certas sutilezas nos gráficos anteriores: * A distância (raio) de um pólo complexo no RL para a opção 1 está um pouco mais próxima da origem do plano-z em comparação com a opção 2. A diferença pode parecer pequena nas figuras, mas as 2 opções implicam resultados bem diferentes.
Conclusão: Optando pela opção 1, porque o RL com pólos complexos fica ligeiramente mais afastado do círculo unitário (resposta + rápida).
Continuando com projeto do PI:
» PI=tf( [1 -0.93], [1 -1], T)
PI =
z - 0.93
--------
z - 1
Sample time: 0.1 seconds
Discrete-time transfer function.
» ftma_PI=PI*BoG;
» figure; rlocus(ftma_PI)
» hold on;
» zgrid(zeta,0)
» % Sintonizando PI:
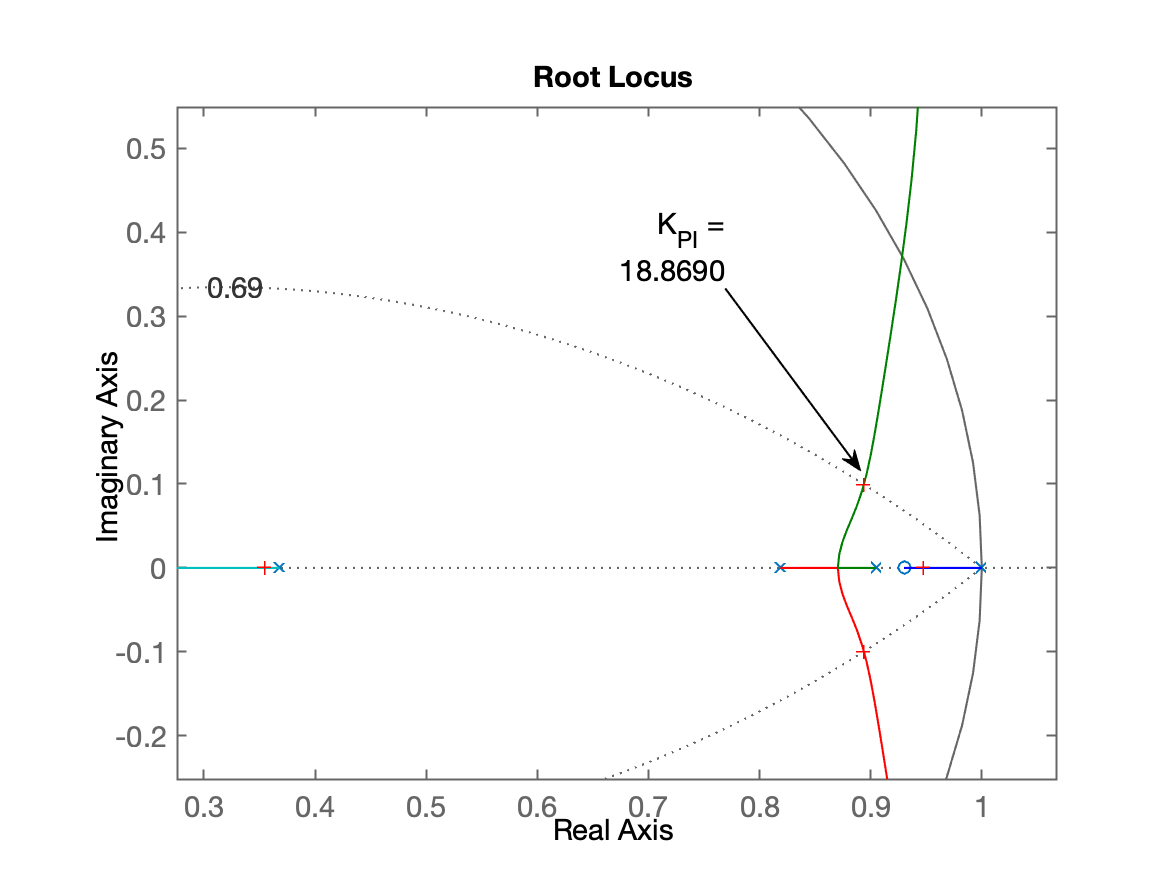
» [K_PI, polosMF] = rlocfind(ftma_PI)
Select a point in the graphics window
selected_point =
0.8938 + 0.0992i
K_PI =
18.8690
polosMF =
0.9472 + 0.0000i
0.8938 + 0.0992i
0.8938 - 0.0992i
0.3543 + 0.0000i
zpk(BoG)
ans =
0.00012224 (z+2.747) (z+0.1903)
--------------------------------
(z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.RL resultante:
Fechando a malha:
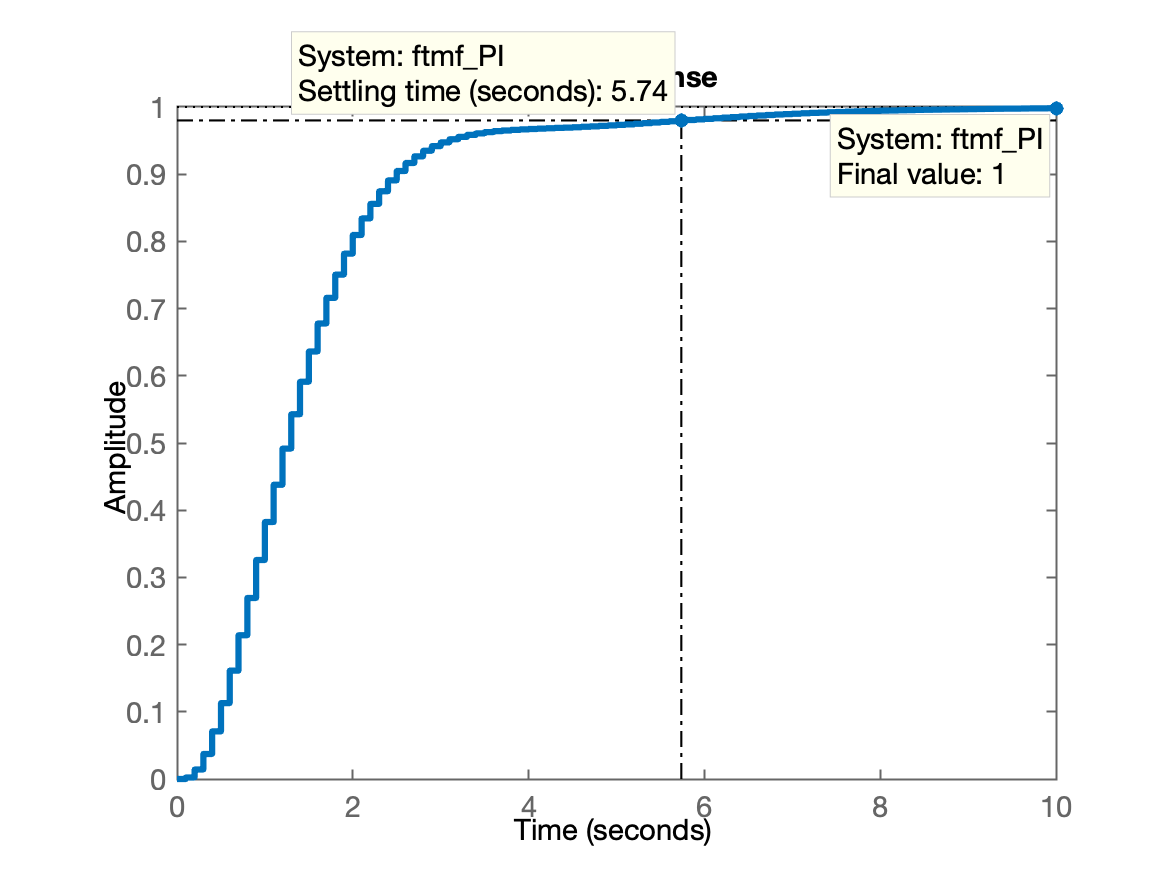
» ftmf_PI = feedback(K_PI*ftma_PI, 1);
» figure; step(ftmf_PI)Resultado da resposta ao degrau:
Comparando com controladores anteriores:
» figure; step(ftmf, ftmf_I, ftmf_PI);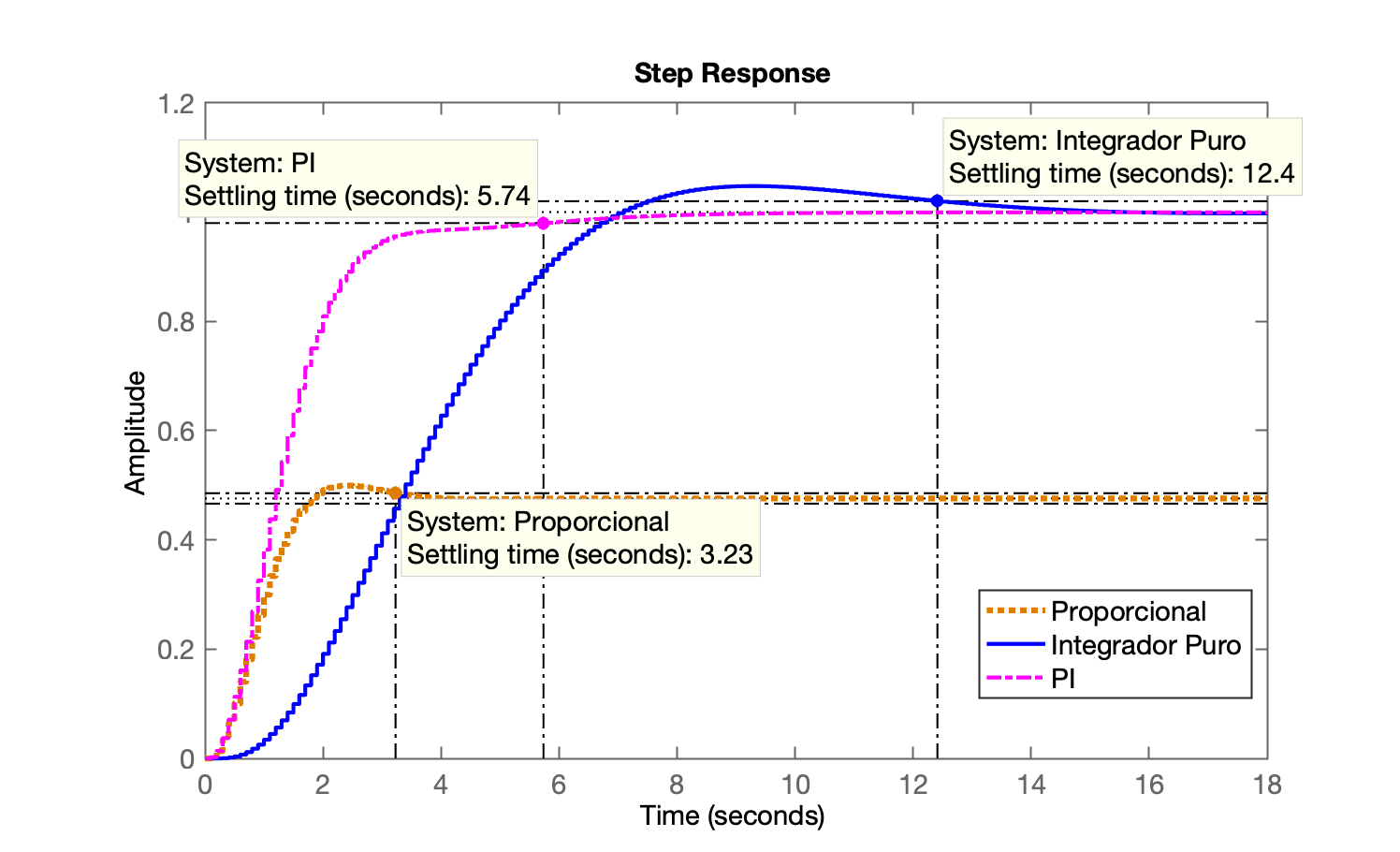
Comparativo do Lag com PI (teoria):
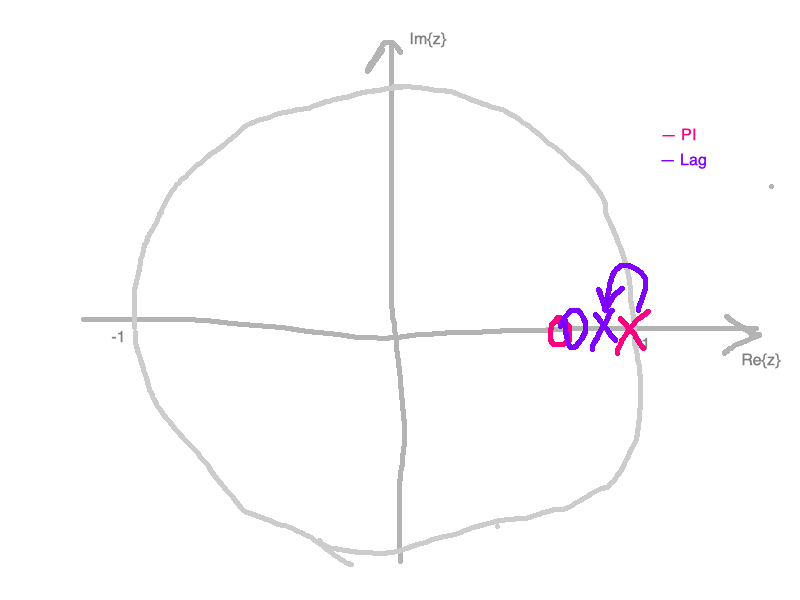
» % Lembrando de BoG(z)
» zpk(BoG)
ans =
0.00012224 (z+2.747) (z+0.1903)
--------------------------------
(z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
» Lag=tf( [1 -0.91] , [1 -0.98 ] , T)
Lag =
z - 0.91
--------
z - 0.98
Sample time: 0.1 seconds
Discrete-time transfer function.
» ftma_Lag=Lag*BoG;
» figure; rlocus(ftma_Lag)
» hold on
» zgrid(zeta,0)
» % Sintonizando Lag:
» [K_Lag, polosMF] = rlocfind(ftma_Lag)
Select a point in the graphics window
selected_point =
0.9009 + 0.0952i
K_Lag =
17.1887
polosMF =
0.9135 + 0.0000i
0.9002 + 0.0953i
0.9002 - 0.0953i
0.3555 + 0.0000iRL resultante para o Lag:
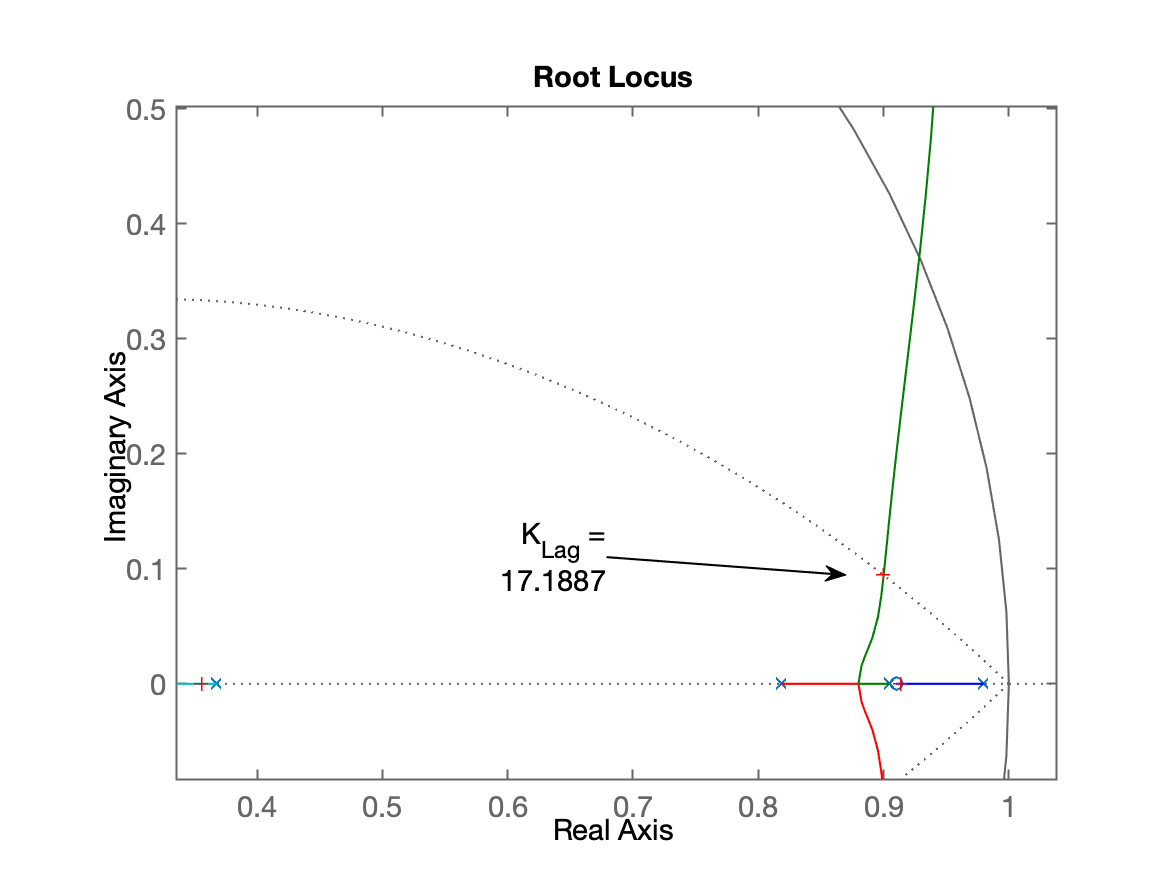
Fechando a malha...
» ftmf_Lag = feedback(K_Lag*ftma_Lag, 1);
» figure; step(ftmf_Lag)
» axis([0 6 0 1])Resposta ao degrau para controlador Lag:
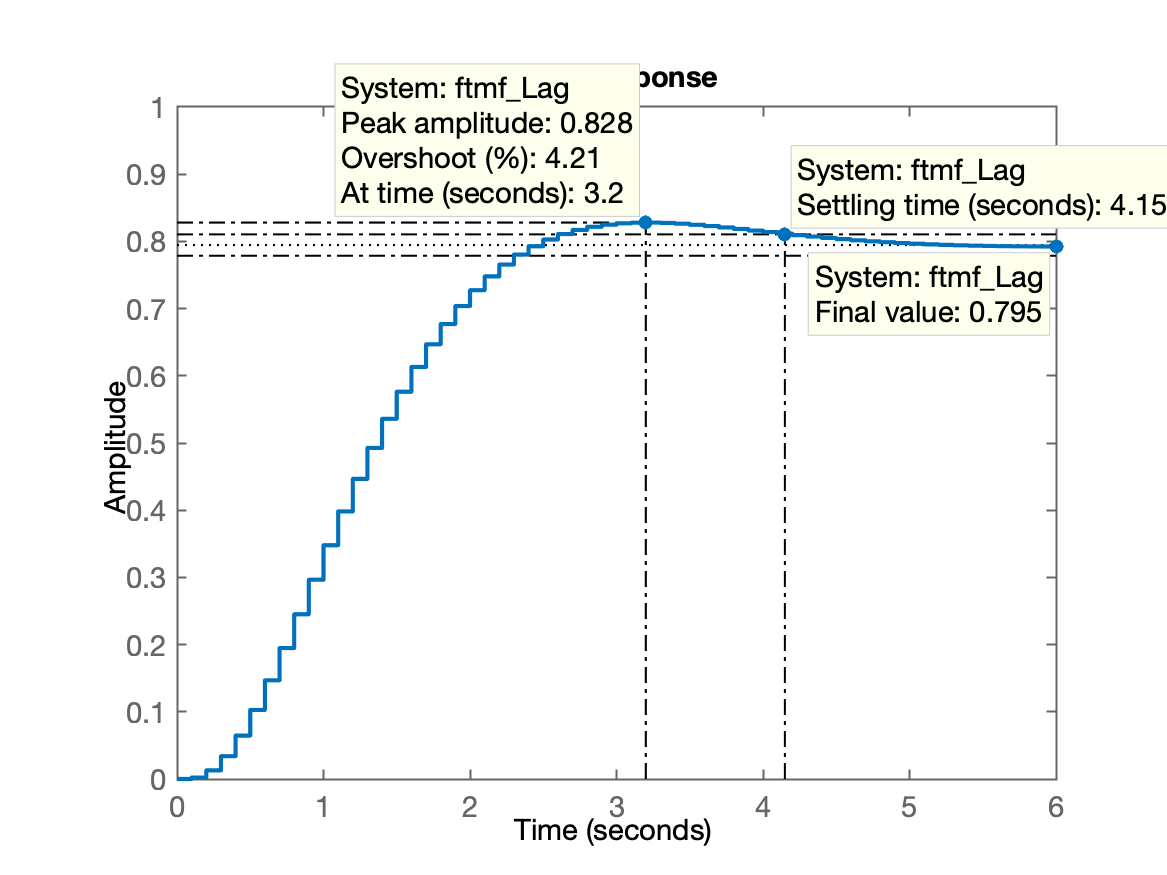
Note, agora existe erro em regime permanente: \(e[kT] \neq 0\).
» % Verificando erro
» dcgain(ftmf_Lag) % valor de y[\infty]
ans =
0.7946
» erro_Lag=(1-dcgain(ftmf_Lag))/1*100
» erro_Lag =
20.5446Comparando Lag com PI:
» figure; step(ftmf_PI, ftmf_Lag)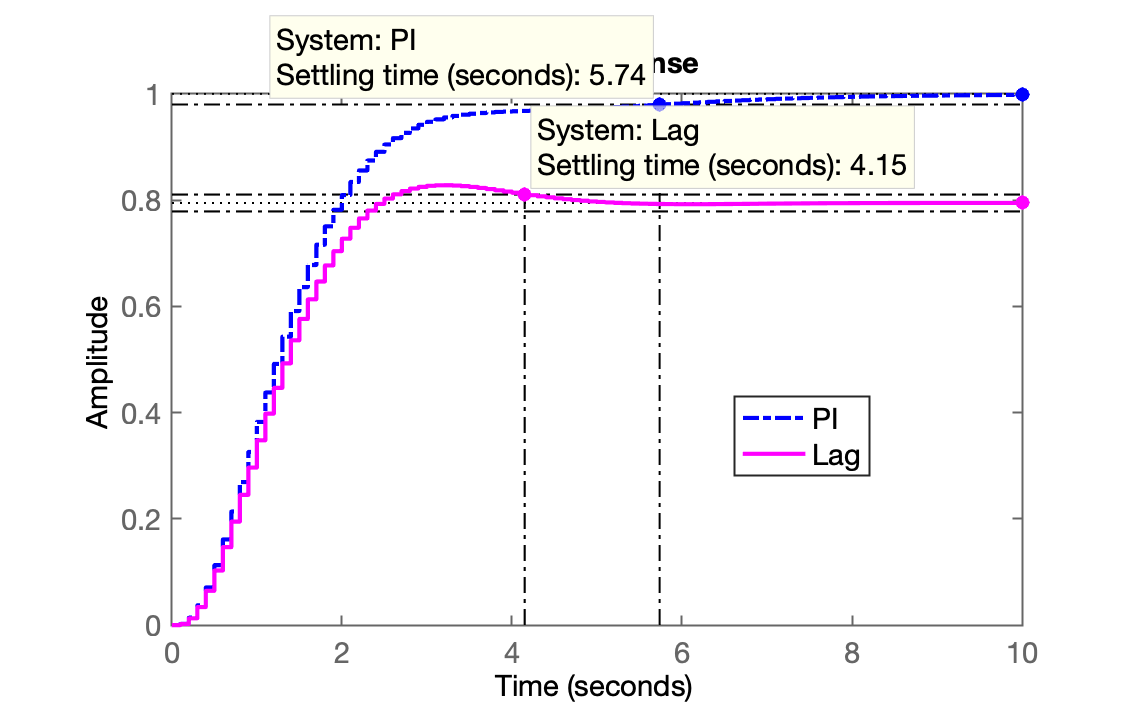
A ideia aqui é avaliar se ao invés de atribuir um local para o zero entre pólos dominantes da \(FTMA(z)\), o que ocorre se o zero do controlador cancelar propositalmente o pólo mais lento da planta?
» polos_planta=pole(BoG)
0.9048
0.8187
0.3679
» polos_planta(1) % isolando apenas o pólo + lento
ans =
0.9048
» % Montando o PI com zero igual ao pólo + lento da planta:
» PI2=tf( [1 -polos_planta(1)], [1 -1], T)
PI2 =
z - 0.9048
----------
z - 1
Sample time: 0.1 seconds
Discrete-time transfer function.
» ftma_PI2=PI2*BoG;
» zpk(ftma_PI2) % comprovando cancelamento pólo-zero
ans =
0.00012224 (z+2.747) (z-0.9048) (z+0.1903)
------------------------------------------
(z-1) (z-0.9048) (z-0.8187) (z-0.3679)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
» figure; rlocus(ftma_PI2)
» hold on;
» zgrid(zeta,0)
» % Sintonizando este PI:
» [K_PI2,polosMF] = rlocfind(ftma_PI2)
Select a point in the graphics window
selected_point =
0.9158 + 0.0845i
K_PI2 =
17.1359
polosMF =
0.9143 + 0.0846i
0.9143 - 0.0846i
0.9048 + 0.0000i
0.3560 + 0.0000iRL resultante:
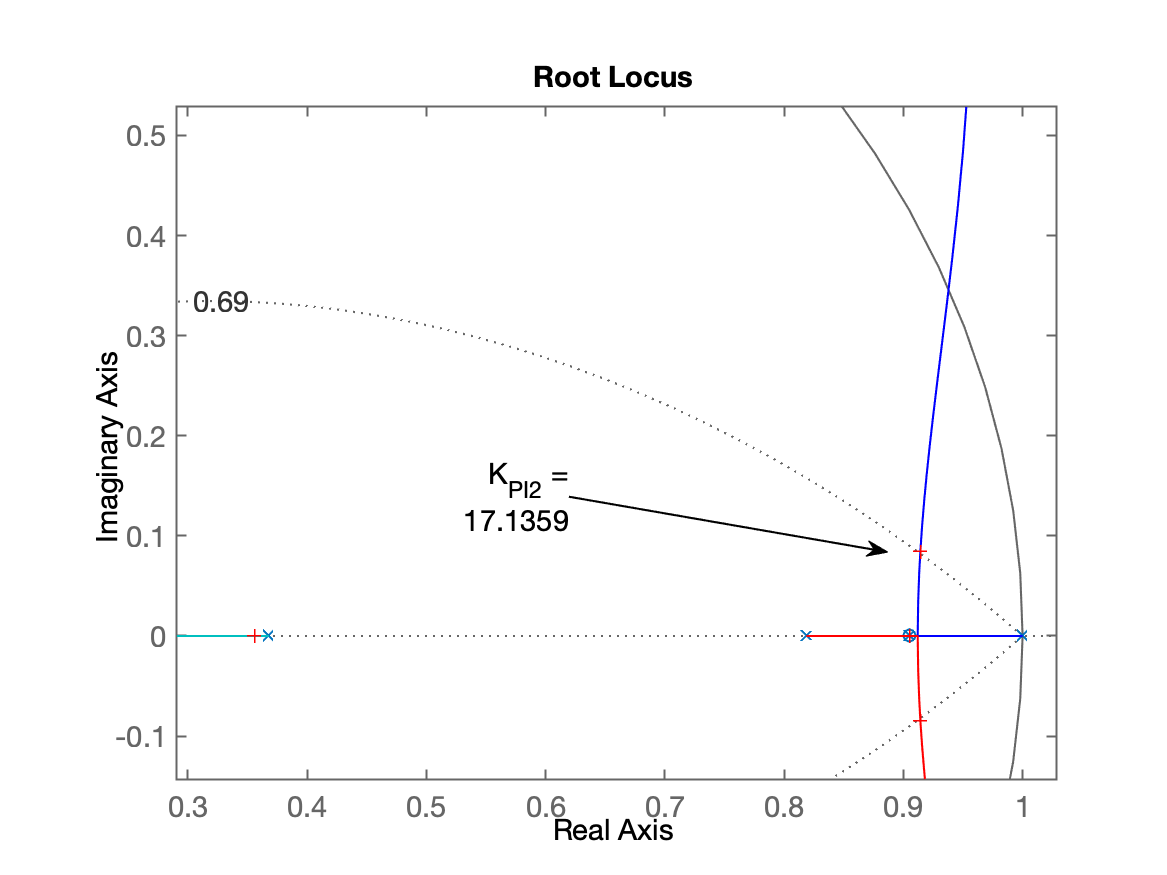
Fechando a malha...
» ftmf_PI2=feedback(K_PI2*ftma_PI2, 1);
» figure; step(ftmf_PI, ftmf_PI2)Resposta ao degrau unitário:
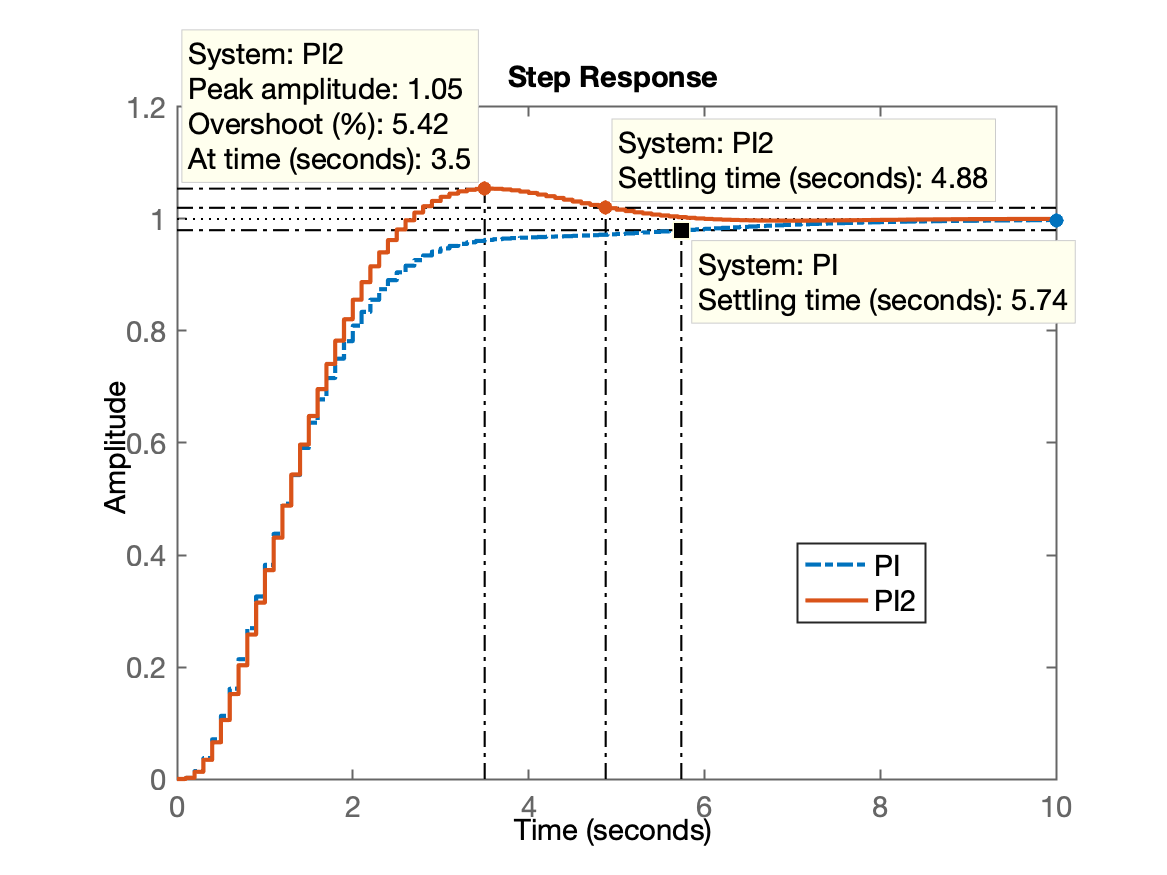
A ideia aqui é avaliar as amplitudes desenvolvidas por cada ação de controle, \(u[kT]\):
Baseado na apostila.pdf (Apêndice G.1 Gráfico de \(u[kT]\)), percebemos que a função step(FTMF) do Matlab realiza: \[ \text{step(FTMF)}=\text{"plot"} \left( \mathcal{Z}^{-1}\left\{ \underbrace{U(z)}_{\mathcal{Z}\left\{ \text{Degrau} \right\}} \cdot \text{FTMF}(z) \right\} \right) \] E lembrando que: \[ U(z)=\left[ \dfrac{C(z)}{1+C(z)\cdot BoG(z)} \right] \] Então:
» aux_PI2=K_PI2*PI2/(1+K_PI2*ftma_PI2);
» aux_PI=K_PI*PI/(1+K_PI*ftma_PI);
» % Comparando $u[kT]$ do PI com PI2:
» figure; step(aux_PI, aux_PI2)
Comparando com controlador proporcional
» aux_Kp=K/(1+K*BoG);
» figure; step(aux_Kp, aux_PI, aux_PI2)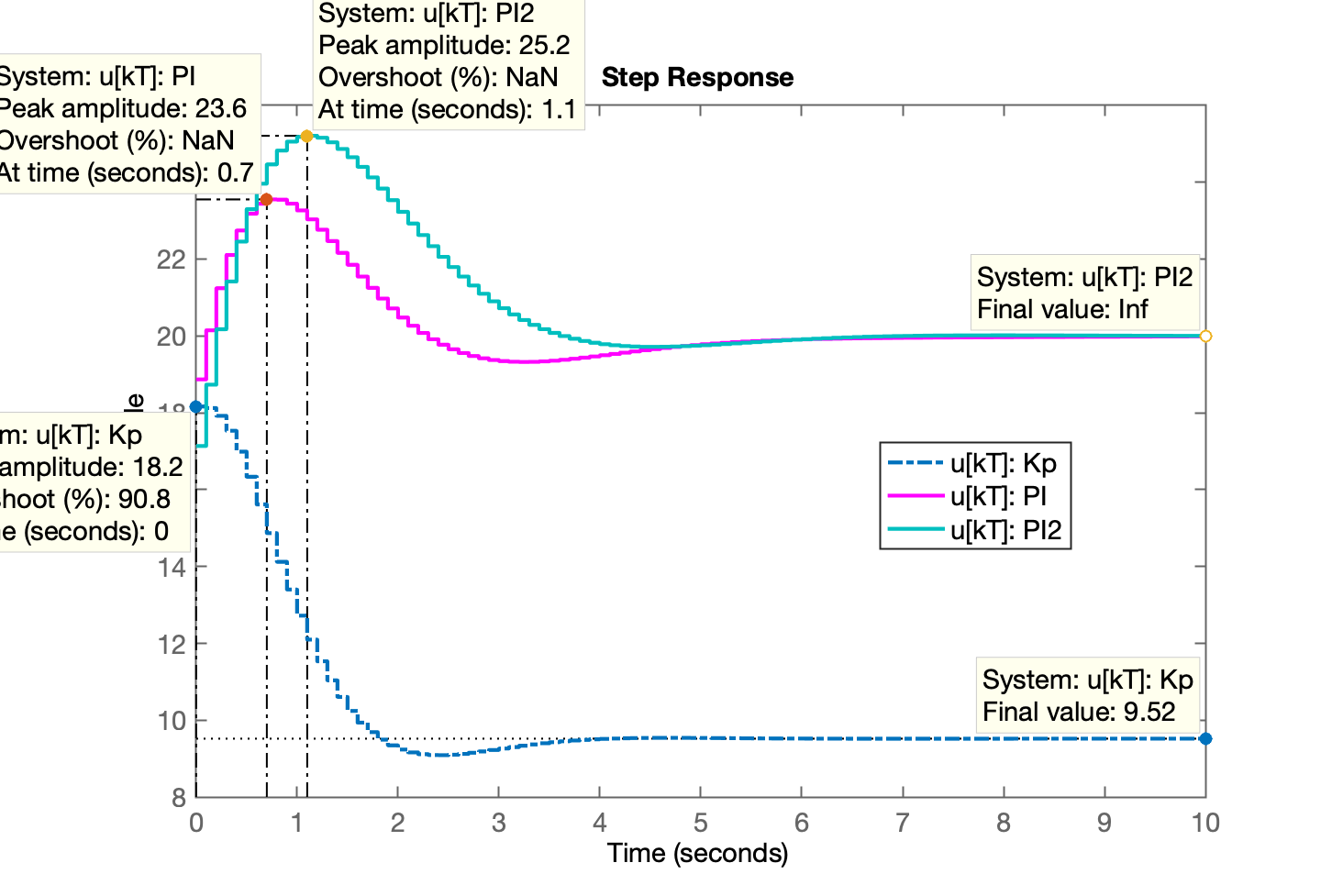
Finalizando atividades desta aula:
» save planta
» diary offFernando Passold, em 14/10/2020