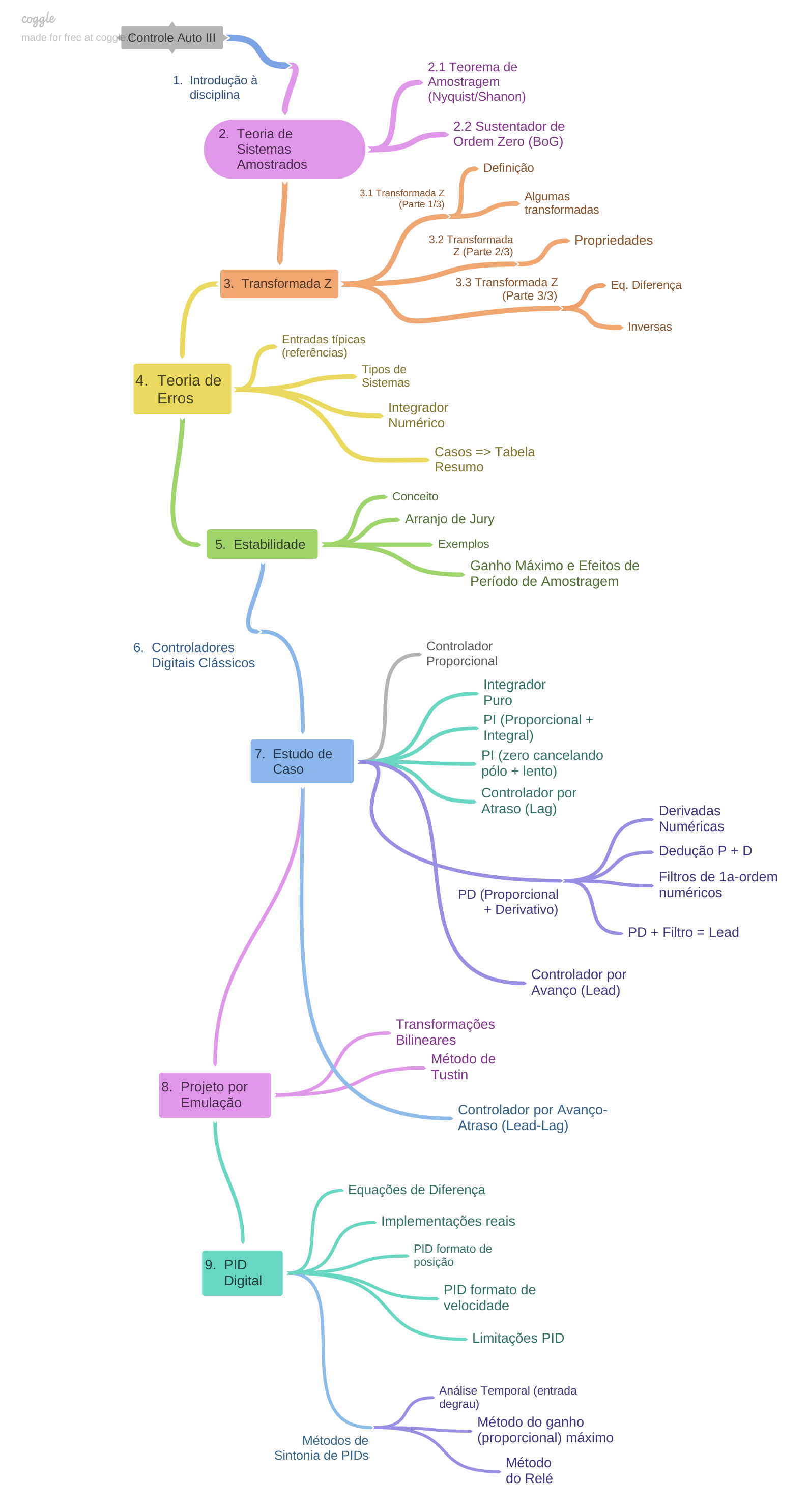
Sequencia Prevista para Aulas de Controle Automático III
1a-Parte:
-
Introdução à Disciplina Material introdutório da disciplina. Organização da Disciplina.
-
Teoria de Sistemas Amostrados Material sobre o processo de digitalização de um sinal. Modelagem de um sinal amostrado (digitalizado). Teoria de Amostragem. Necessidade de filtros passa-baixa analógicos antes e após a digitalização. Efeitos de sub-amostragem (aliasing).
- Sustentador de Ordem Zero (
). Modelagem do sustentador de ordem zero. Como incorporar/deduzir BoG(z).
- Sustentador de Ordem Zero (
-
Transformada-Z
- Definição, Limitações, transformadas-Z de sinais limitados no tempo
- Transformadas Z da função Impulso, função Degrau (revisão de PG), de função Exponencial (convergente ou divergente). Respostas de alguns sinais no padrão
. - Transformada Z de uma Senóide, de uma Senóide Amortecida.
- Propriedades da Transformada Z: Linearidade, Avanço no tempo, atraso no tempo, translação complexa, convolução, teorema do valor inicial, teorema do valor final. Exemplos.
- Transformada Z Inversa. Trata sobre métodos de transformada Inversa de Z. Método da divisão longa. Método baseado em tabelas de transformada relacionando plano-s e plano-z e expanção em frações parciais. Exemplos.
- Representação de Sistemas Discretos. Revisão de equações de diferença e equações diferenças para uso no projeto de controladores digitais no plano-z. Material original em inglês. 4 páginas.
2a-parte (principal) da disciplina:
- Teoria de Erros;
- Estabilidade;
- Controladores Digital Clásssico;
- Projeto de Controladores: Estudo de Caso (vários Controladores), inclui controlador Dead-beat;
- Projeto por Emulação (usando transformações bilineares);
- PID digital
- início à introdução de Controle no Espaço de Estados (controle moderno). -->
Seguem-se Anexos:
A) Equações; B) Respostas temporais no plano-Z; C) Transformada-Z usando MATLAB; D) Respostas ao Degrau; E) Revisão de Controladores Clássicos; F) Comandos do MATLAB e G) Gráficos de u[kT] e e[kT].
Segue mapa conceitual (ou road-map) da disciplina na figura abaixo:
Fernando Passold