Projeto de Controladores usando Root Locus (Parte I)

Conteúdo previsto:

• Introdução:

  • Limitações no Ajuste do Ganho;
  • Reduzindo erro estacionário;
  • Melhor Resposta Transitória;
  • Menor Erro Estacionário (ou de Regime Permanente)

• Controladores com Ação Integral

  • Ação Integral Pura
  • Exemplo de controlador Proporcional x Integrador Puro
  • Controlador PI (Proporcional + Integral)

Objetivos:

• Projeto de compensadores em cascata para melhorar erro estacionário;
• Projeto de compensadores para melhorar resposta transitória;
• Projeto de compensadores para melhorar tanto o erro estacionário quanto a resposta transitória

Limitação no Ajuste do Ganho

• Ajustar o ganho para determinado valor leva a uma resposta transitória que depende da localização final dos pólos em malha-fechada (MF);
• Geralmente o projeto de cada controlador fica limitado à respostas que somente posicionam pólos ao longo do RL (Root Locus);
• Formas de resolver esta limitação:
  • Aumentar a complexidade de compensador, introduzindo pólos e zeros, de modo que o sistema compensado possua pólos de MF localizados em pontos desejados, com ajuste desta posição dependendo de certo valor do ganho.

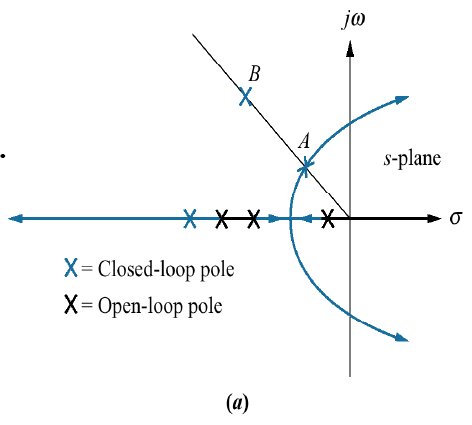
Exemplo: Observe as próximas figuras e acompanhe o raciocínio:

Seja um sistema que resulta no seguinte RL:

seu comportamento temporal correspondente seria:

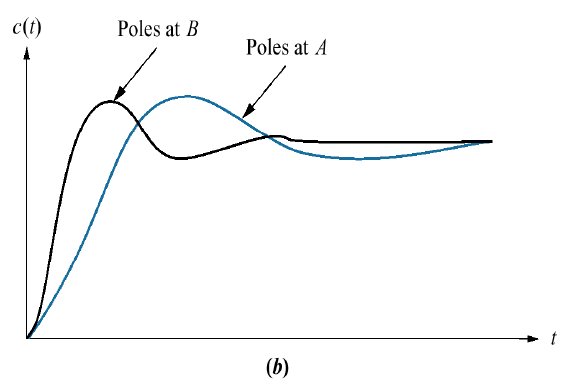
Note:

• Pode-se acelar o sistema deixando de optar pelo pólo na posição A e optando pela posição B; note que sem afetar o percentual de sobressinal (overshoot);
• Este aumento na velocidade de resposta pode ser obtido modificando a posição dos pólos de MF;

Reduzindo erro estacionário

• Introduzir compensadores na malha de realimentação:

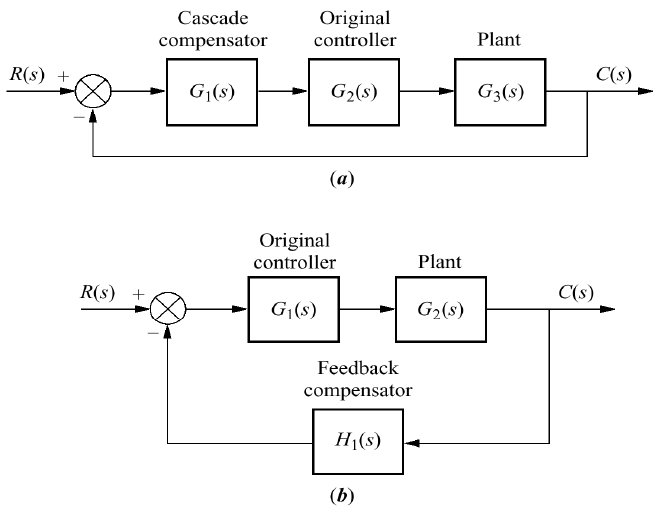
2 configurações:

a) Em cascata;

b) Presente na realimentação

Reduzindo Erro Estacionário com Compensador em Cascata

• 2 maneiras de melhorar o erro estacionário:

  • Usando um compensador PI;
  • Usando compensador por Atraso de Fase (Lag);

• Compensandor PI (Proporcional + Integrativo):

  • Utilizar um integrador puro (rede ativa, usando amplificadores operacionais), introduzindo na malha direta (FTMA), um pólo na origem do plano-s;
  • Isto aumenta a ordem do sitema, mas anula o erro (ao menos para entrada degrau).

• Compensador por Atraso de Fase (Lag):

  • Se usa uma rede passiva para acrescentar um pólo e posicioná-lo próximo da origem do plano-s;
  • Não anula o erro nulo de regime permanente mas reduz seu valor significativamente.

Exemplos

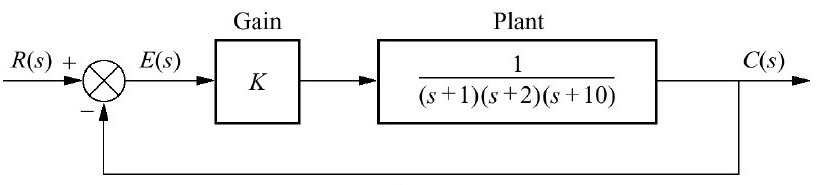
Vamos trabalhar com a seguinte planta:

\[ G(s)=\dfrac{1}{(s+1)(s+2)(s+10)} \]

Note que é um sistema tipo 0, sem integrador, portanto, pela teoria do erro, pode-se esperar erro limitador para entradas degrau enquanto não for acrescentada alguma ação integral ao sistema.

A idéia é:

1. Fechar uma malha com Controlador Proporcional, limitando o sobressinal máximo à 20%;
2. Fechar malha com controlador Integral Puro, mesma limitação de overshoot;
3. Fechar malha com PI, mesma limitação de overshoot;

Comparando resultados obtidos.

Raciocínio preliminar

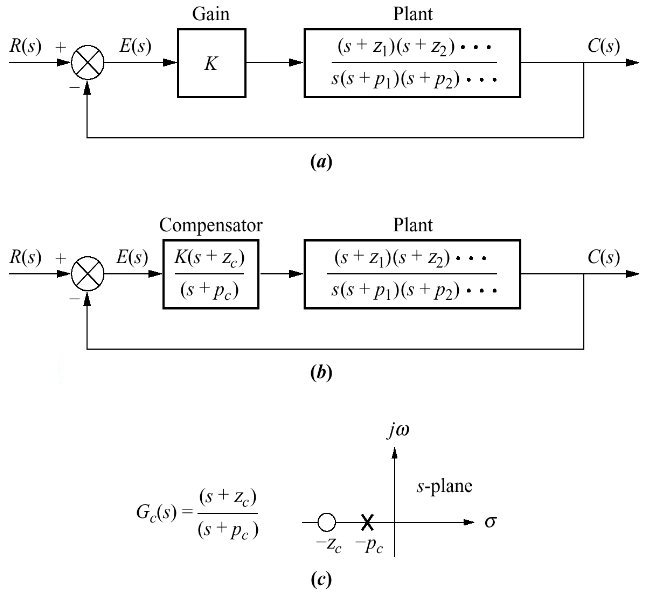
Note que o RL para os 2 primeiros controladores resulta nos seguintes RL's:

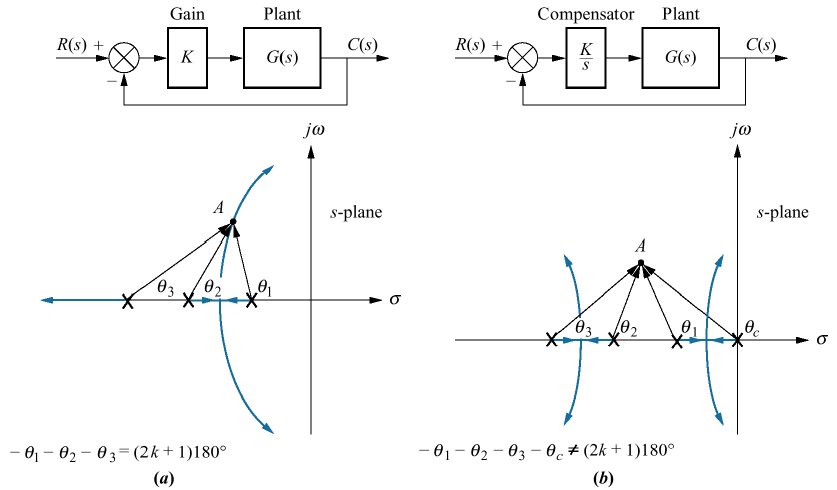
Note que o simples fato de acrescentar um pólo na origem modificou o RL original (a) para o RL mostrado na figura (b).

O ponto A na figura corresponde à determinada posição desejada para os pólos de MF. Para definir esta posição, além de sabermos o \(\zeta\) desejado, também necessitamos mais resquisitos de controle associados com tempos de resposta (\(t_s, t_r, t_p\)).

Note que se for desejado determinar com precisão a posição do ponto A na figura (a), teremos que realizar cálculos trigonométricos associados com contribuição angular provovadas pelos pólos e zeros presentes num sistema (lembrar das regras básicas de RL); algo como:

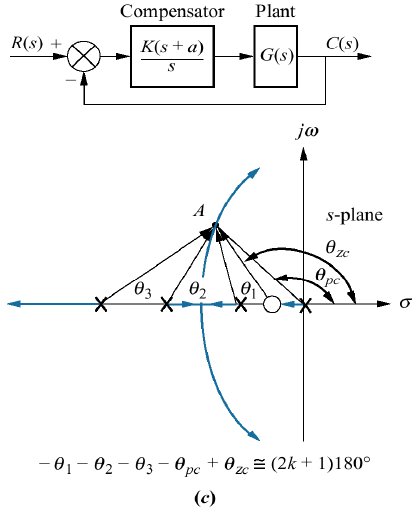
Esta última figura mostra o projeto de um PI usando contribuição angular. No caso deste controlar, sabemos à priori onde deve estar localizado seu pólo (na origem), mas não sabemos onde devemos localizar seu zero. Note pela figura, que o cálculo dos ângulos apresentados, objetiva descobrir qual o ângulo que deveria ser assumido pelo zero do PI, variável \(\theta_{zc}\). Sabe-se que para o ponto A pertencer a um traço do RL, os ângulos formados pelo mesmo devem obedecer à seguinte regra básica do RL:

\[ \sum_{i=1}^{\text{Zeros}} \theta_{z_i} - \sum_{j=1}^{\text{Polos}} \theta_{z_j}=(2k+1)180^o \]

ou em radianos (Matlab):

\[ \sum_{i=1}^{\text{Zeros}} \theta_{z_i} - \sum_{j=1}^{\text{Polos}} \theta_{z_j}=(2k+1)\pi \]

Então no caso da figura (c), usando contribuição angular, conseguimos descobrir o ângulo do zero, \(\theta_{zc}\) e assim, usando trigonometria (arco tangente) se pode determinar onde deve estar loocaliza a parte real deste zero.

Projeto do Controlador Proporcional

O diagrama em blocos deste sistema fica:

Resolvendo:

>> % Seguem comandos no Matlab

Projeto do Controlador Integral Puro

Resolvendo:

>> % Seguem comandos no Matlab

Projeto de Controlador PI

Num primeiro momento vamos simular o seguinte diagrama em blocos:

Note que o zero do controlador foi colocado (arbitrariamente) em \(s=-0,1\).

Note a origem da equação do PI:

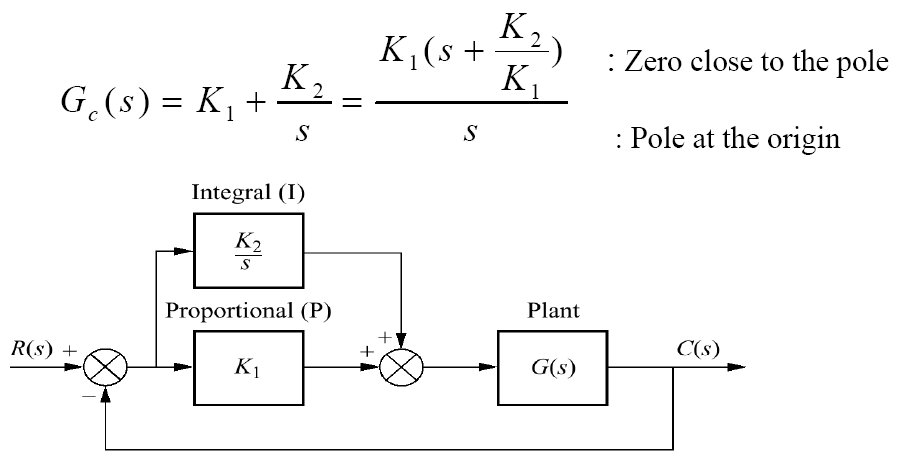
Note que \(K_1=K_p\) (ganho proporcional) e que \(K_2=K_i\) (ganho integral).

Resolvendo:

>> % Seguem comandos no Matlab

Mais tarde, numa próxima etapa, vamos modificar um pouco o controlador PI, para um controlador por Atraso de Fase (Lag), como mostra a figura à seguir:

Note que neste caso, o pólo do controlador já não está sobre a origem do plano-s, mas muito próximo da origem do plano-s, o que implica num comportamento semelhante ao de uma ação integral.

Anexos: Equações

Segue um "compêndio de equações" baseadas numa resposta típica sub-amortecida para sistemas de MF de segunda ordem.

As equações à seguir valem para um sistema do tipo:

\[ FTMF(s)=\dfrac{\omega_n^2}{s^2+2\zeta\omega_n s + \omega_n^2}=\dfrac{b}{s^2+as+b} \]

Considerando pólos complexos em MF (\(0 < \zeta < 1\)) teremos:

Pólos de MF localizados em: \(s=-\sigma \pm j \omega_d\), onde \(\omega_d=\omega_n \sqrt{1-\zeta^2}\).

A resposta temporal fica:

\[ y(t)=1-\exp\left( -\zeta \omega_n t\right) \left[ \cos\left( \omega_d t\right) + \dfrac{\zeta}{\sqrt{1-\zeta^2}} \sin \left( \omega_d t\right) \right] \]

O overshoot fica:

\[ \%OS=\exp \left( \dfrac{-\zeta}{\sqrt{1-\zeta^2}} \right) \times 100\% \]

isolando \(\zeta\) em função de \(\%OS\):

\[ \zeta=\dfrac{-ln \left( \%OS/100 \right)}{\sqrt{\pi^2+\ln^2 \left( \%OS/100 \right)}} \]

ou \(\zeta=\cos(\alpha)\), ver figura à seguir:

Outras equações relacionando medidas temporais:

\[ t_p=\dfrac{\pi}{\omega_n \sqrt{1-\zeta^2}}=\dfrac{\pi}{\omega_d} \]

\[ t_s=\dfrac{-\ln \left( 0,02 \sqrt{1-\zeta^2} \right)}{\zeta \omega_n} \]

\[ t_s=\dfrac{4}{\zeta \omega_n}=\dfrac{4}{\sigma} \quad \text{ para: } 0 < \zeta < 1 \]

\[ t_r=\dfrac{0,6+2,16 \zeta}{\omega_n} \]

O que pode ser simulado no Matlab via função ord2(wn,z):

>> OS=20; % overshoot de 20%
>> ts=2;  % tempo de assentamento de 2 segundos
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
    0.4559
>> wn=4/(zeta*ts) % resposta em rad/s
wn =
    4.3864
>> [num_mf,den_mf]=ord2(wn,zeta)
num_mf =
     1
den_mf =
    1.0000    4.0000   19.2409
>> ftmf=tf(num_mf,den_mf);
>> zpk(ftmf)

ans =
 
          1
  ------------------
  (s^2 + 4s + 19.24)
 
Continuous-time zero/pole/gain model.

>> % comprovando a resposta temporal
>> step(ftmf)
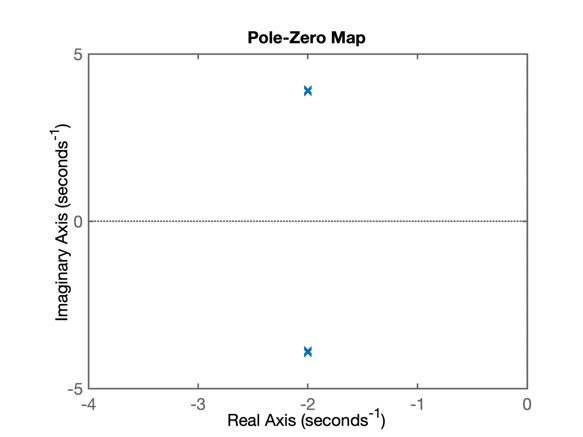
>>> polos_MF=pole(ftmf)
polos_MF =
  -2.0000 + 3.9040i
  -2.0000 - 3.9040i
>> figure; pzmap(ftmf)
>> axis([-4 0 -5 5])

Que gera o gráfico:

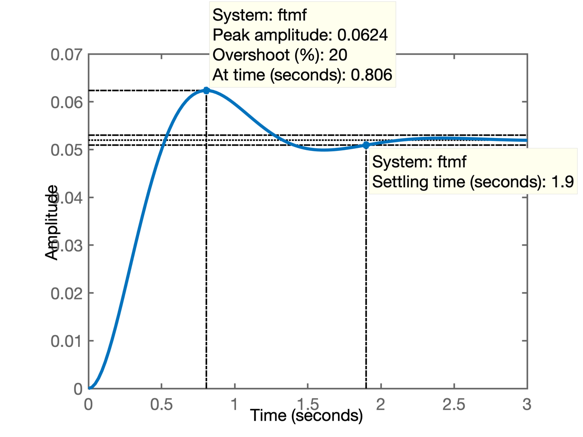
que refleto o que ocorre no domínio tempo quando os pólos abaixo são submetidos à uma entrada degrau:

Fernando Passold, em 12/05/2020