Cuidados em cálculo de ângulos associados com Contribuição Angular no RL:
Reparem como são calculados os ângulos:
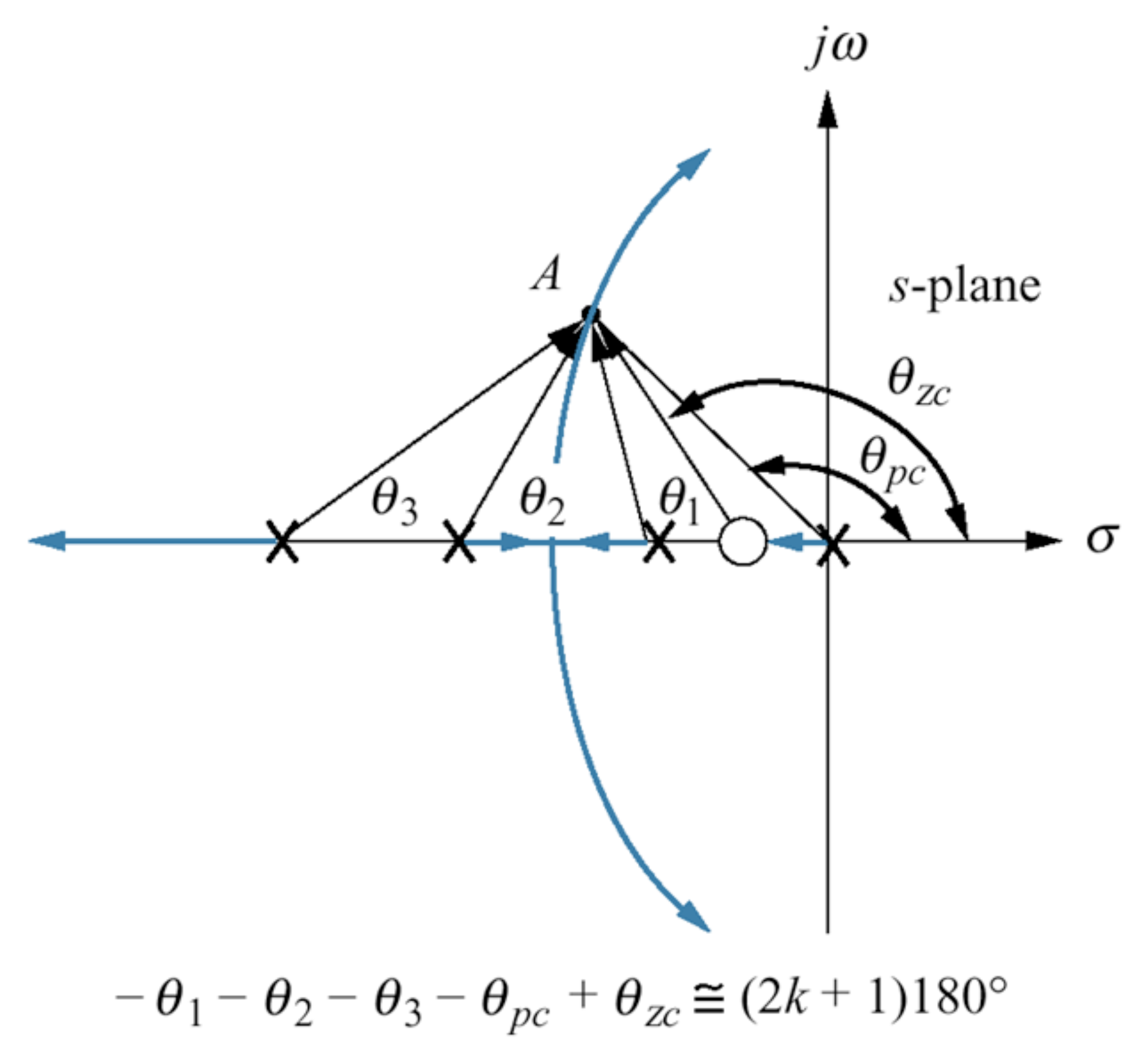
Note como é definida a regra que confirma que certo ponto (polo de malha fechada na posição desejada) pertence a uma curva do RL:
Isto significa que a contribuição angular resultante do somatório dos ângulos dos zeros menos o somatório dos ângulos dos polos deve gerar um número ímpar associado com os 180, ou seja, o resultado das contribuições angulares deve resultar no ângulo de:
ou
Ou, na forma de um gráfico “rudimentar”, ver figura a seguir:
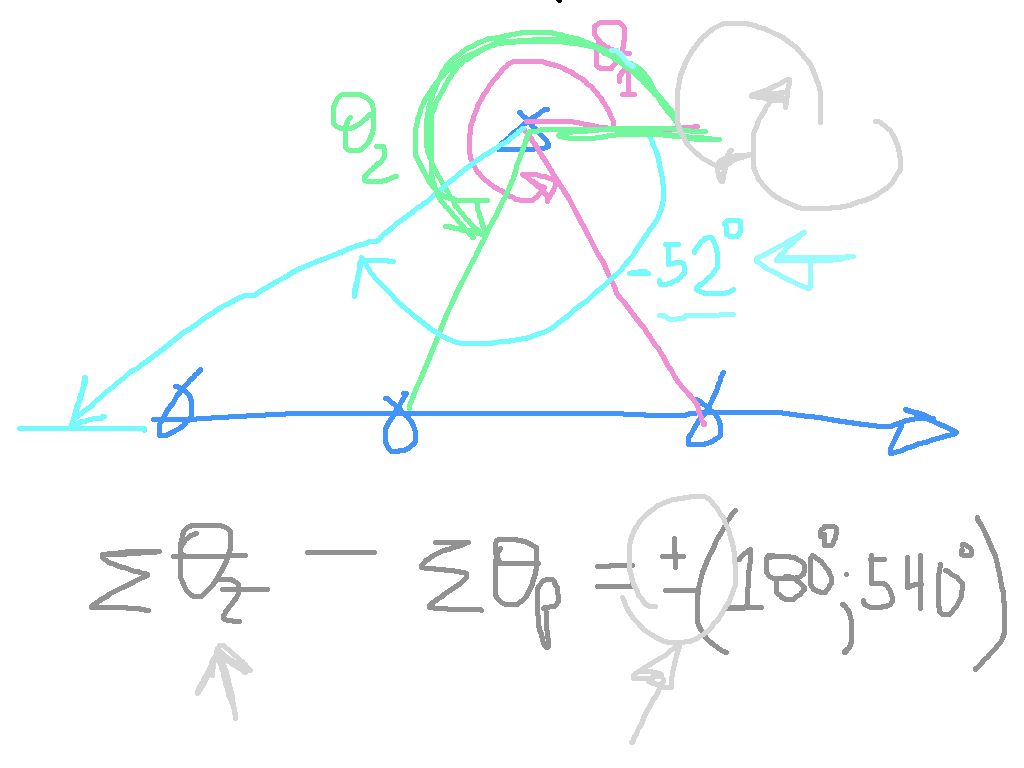
Note que o termo “" gera variações no momento de calcular um ângulo.
Por exemplo, no caso do projeto do PD para a planta de 3a-ordem que não possui zeros, o único ângulo referente a um zero é do próprio zero do PD que está sendo buscado. A equação (1) fica então como:
isolando o termo , teremos:
e na continuação:
Note que para encontrar o valor do ângulo do zero do PD você pode optar pela eq. (2a) ou (2b). O resultado no gráfico deve ser o mesmo, independente da equação usada.
Mas... você ainda deve tomar algum cuidado quando finaliza o cálculo para determinação da posição do zero do PD. A eq (2a) ou (2b) vai lhe permitir identificar o ângulo que o zero do PD deveria ter em relação aos pólos malha fechada.
Para calcular a posição deste zero você pode fazer:
Onde: é a parte imaginária do pólo de MF desejado; é o resultado obtido através da aplicação da eq. (2a) ou (2b); é a parte real do pólo de MF desejado; e corresponde então à localização final do zero do PD.
Recomenda-se atenção com os sinais adotados para os termos explicados anteriormente e seu impacto no resultado final.
Por exemplo:
>> sum_th_p % exibir somatório ângulos dos polos
sum_th_p =
4.0552
>> sum_th_p*180/pi % valor em graus
ans =
232.3460
>> th_c = sum_th_p - pi % aplicando eq. (2b)
th_c =
0.9136
>> th_c*180/pi % angulo do zero do PD (em graus)
52.3454
>> sigma_pd = sigma - (omega/tna(pi - th_c)) % eq. (3)
sigma_pd = 3.7128
>> num_pd = [1 sigma_pd]; % montando polinomio numerador do PDNote que a variável sum_th_p ser refere ao somatório dos ângulos formados pelos pólos na FTMA(s) deste sistema (4,0552 rad = 232,346).
A linha th_c = sum_th_p - pi está aplicando (corretamente) a equação (2b) e foi encontrado o valor: th_c = 0,9136 rad = 52,3454. Até este ponto não existe nenhum erro.
Não tenho acesso à toda sequencia de comandos que gerou os valores de sigma e omega usados originalmente, mas a determinação de onde deveriam estar os pólos de MF deste sistema para e (segundos), leva aos pólos de MF na posição:
Ou
sigma = -1.4815
omega = 2.8918
Então será considerado sum_th_c = ( = 4.0552 radianos ) o que leva à:
| Realizado | O que poderia ter sido realizado também |
|---|---|
| >> th_c = sum_th_p - pi | |
| th_c = | |
| 0.9136 | -- |
| >> th_c*180/pi | |
| ans = | |
| 52.3458 | |
| sigma = + 1.4815 | sigma = - 1.4815 |
| Note o que ocorre | |
| >> sigma_pd = sigma - (omega/tan(pi - th_c)) | >> sigma_pd = sigma - (omega/tan(th_c - pi)) |
| sigma_pd = | sigma_pd = |
| 3.7128 | -3.7128 |
| Note a sutil diferença nas 2 equações acima: | |
O termo omega/tan(pi-th_c)=Delta_x resulta em: |
|
| >> omega/tan(pi - th_c) | >> omega/tan(th_c - pi) |
| ans = | ans = |
| -2.2314 | 2.2314 |
Comparando-se os resultados obtidos, com excessão do sinal do termo sigma_pd, o valor alcançando resulta no mesmo.
Importante notar que o cálculo da contribuição angular faça sentido:
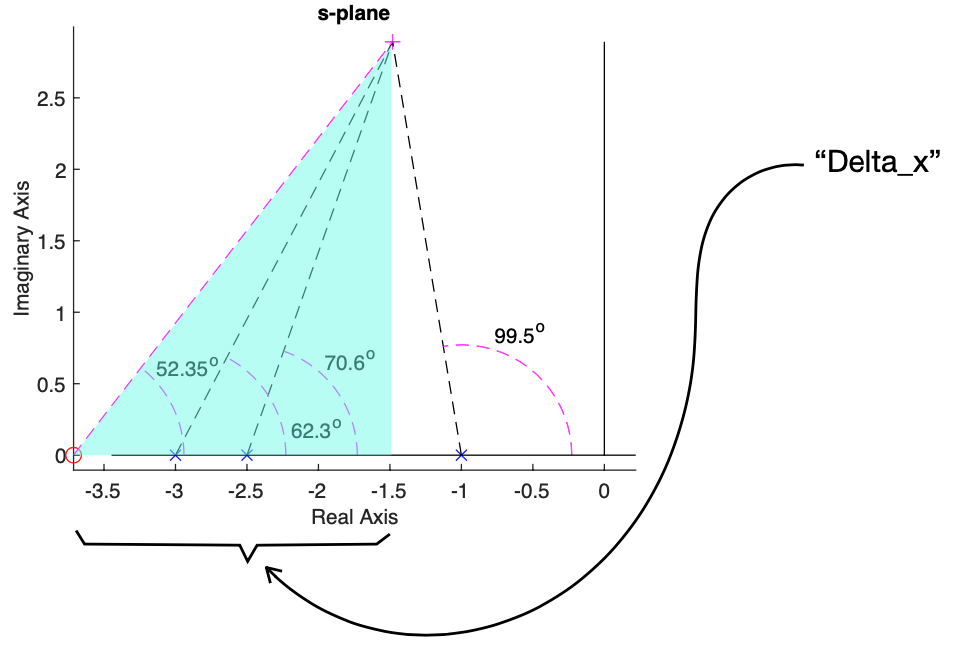
E que o RL no momento de sintonizar o controlador, passe realmente sobre os pólos de MF desejados:
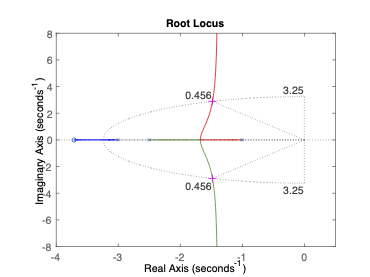
Prof. Fernando Passold, em 01/07/2020.