
Fonte: [Sky Folk]
#Exemplos de Projetos
Referentes ao Projeto de Controladores usando método do Lugar Geométrico das Raízes (ou Root-Locus).
Índice:
Planta 1:
Requisitos de controle:
- (segundos);
- ;
- ;
- , mas: .
Ingressando com os dados daplanta no Matlab:
x>> den1 = conv( [0 1 10], [1 2 2] );>> G1 = tf ( 40*[1 6], 3*den1);>> zpk(G1)ans = 13.333 (s+6) --------------------- (s+10) (s^2 + 2s + 2) Continuous-time zero/pole/gain model.>> 40/3ans = 13.3333>> Calculando fator de amortecimento, , em função do overshoot, :
xxxxxxxxxx>> format compact % matlab mostra resultados de forma mais compacta>> OS=10;>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))zeta = 0.5912>>a) Controlador Proporcional
Sintonizando controlador Proporcional:
xxxxxxxxxx>> % sintonizando controlador proporcional>> rlocus(G1)>> hold on;>> sgrid(zeta,0)>> % fazendo apropriado zoom no gráfico do RL>> [K, polosMF]=rlocfind(G1)Select a point in the graphics windowselected_point = -1.0434 + 1.4125iK = 0.1321polosMF = -9.9143 + 0.0000i -1.0428 + 1.4126i -1.0428 - 1.4126iO que gera o gráfico:
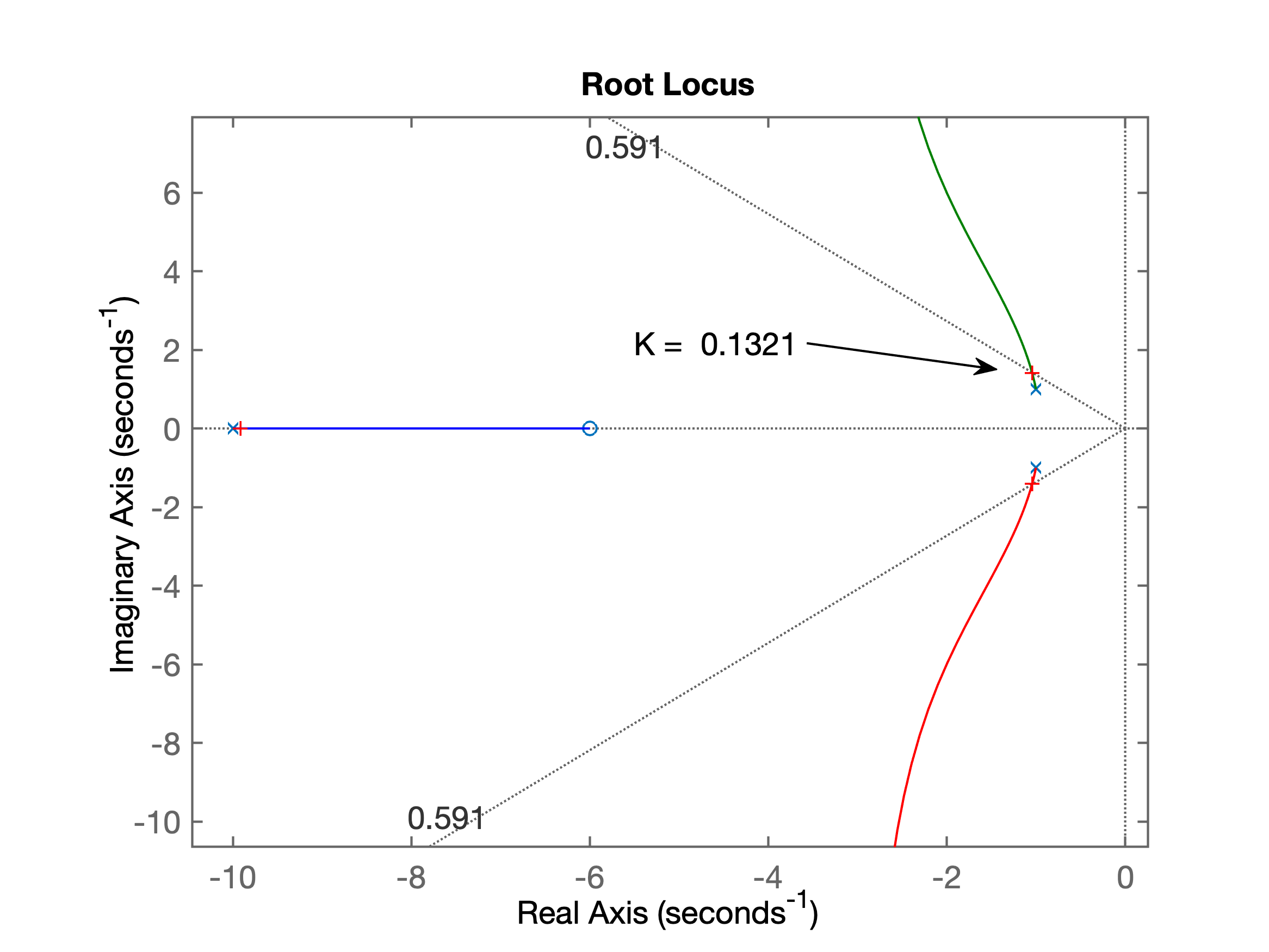
xxxxxxxxxx>> % fechando malha...>> ftmf_Kp=feedback(K*G1, 1);>> % verificando resposta>> figure; % abrindo outra janela gráfica >> step(ftmf_Kp)>> % Verificando $y(\infty)$>> >> dcgain(ftmf_Kp)ans = 0.3456>> erro_Kp=(1-dcgain(ftmf_Kp))*100erro_Kp = 65.4361>> Segue gráfico da resposta ao degrau para controlador proporcional:
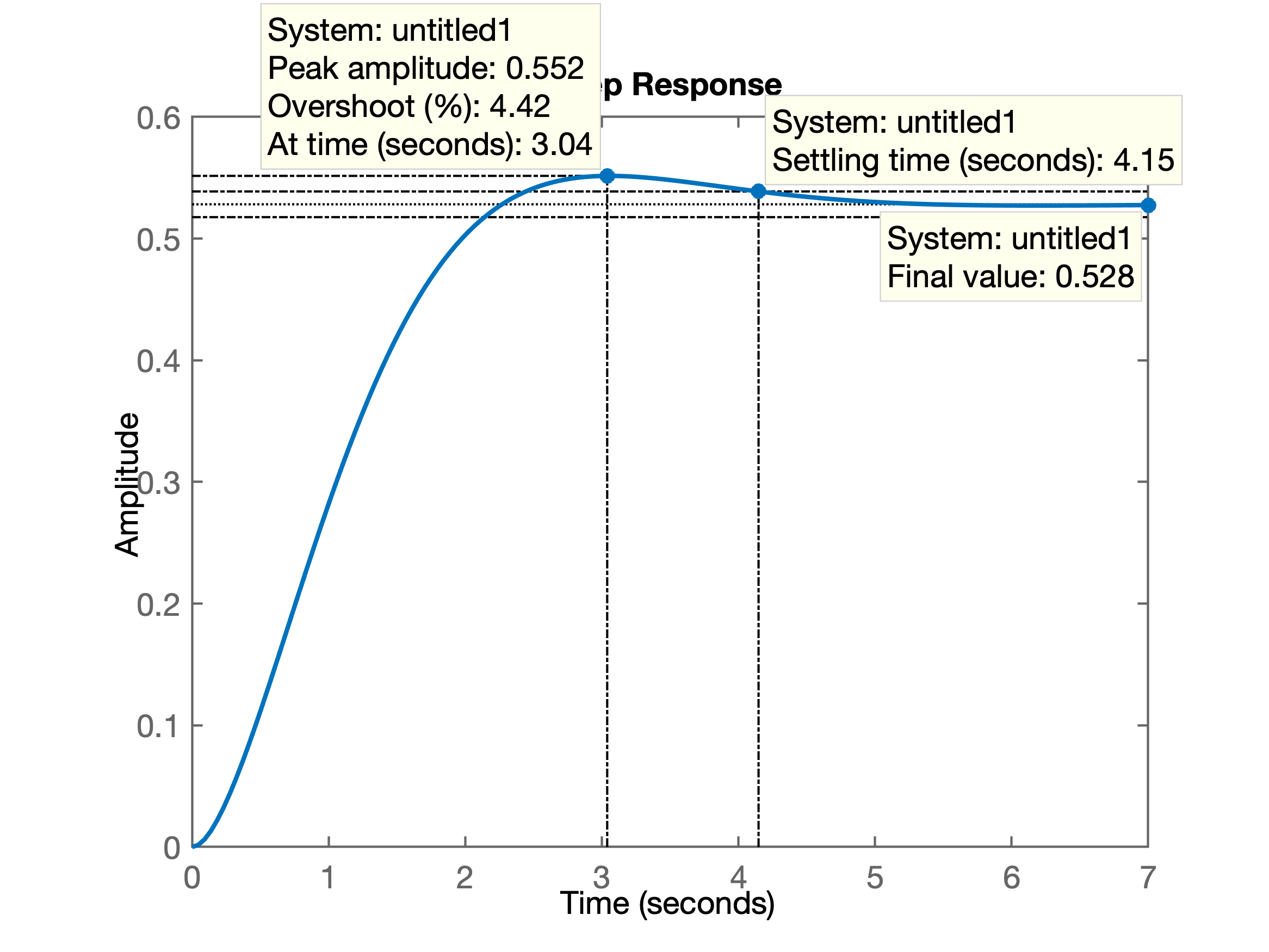
Resumo dos resultados obtidos com Controlador Proporcional:
- em
- Erro de: obiviamente este controlador resulta num enorme erro em regime permanente.
Partindo para outros controladores:
b) Integrador Puro
Equação deste controlador:
No Matlab:
xxxxxxxxxx>> % incorporando controlador integrador puro>> C_I=tf( 1, [1 0]);>> zpk(C_I)ans = 1 - s Continuous-time zero/pole/gain model.>> Fechando a malha e sintonizando Integrador puro:
xxxxxxxxxx>> % fechando malha com Integrador Puro>> ftma_I=C_I*G1;>> % confirmando a FTMA(s):>> zpk(ftma_I)ans = 13.333 (s+6) ----------------------- s (s+10) (s^2 + 2s + 2) Continuous-time zero/pole/gain model.>> % traçando o lugar das raízes>> figure; rlocus(ftma_I)>> % salvo na figura: G1_rlocus_I_puro.png>> hold on; zgrid(zeta,0);>> % realizando o zoom na área de interesse>> % para posteriormente definir o ganho do controlador>> [K_I, polosMF]=rlocfind(ftma_I)Select a point in the graphics windowselected_point = -0.6261 + 0.8493iK_I = 0.1041polosMF = -10.0068 + 0.0000i -0.6275 + 0.8567i -0.6275 - 0.8567i -0.7382 + 0.0000i>> % figura salva como: G1_rlocus_I_puro.pngSegue gráfico do RL com o Integrador Puro, já mostrando o ganho usado para sua sintonia.
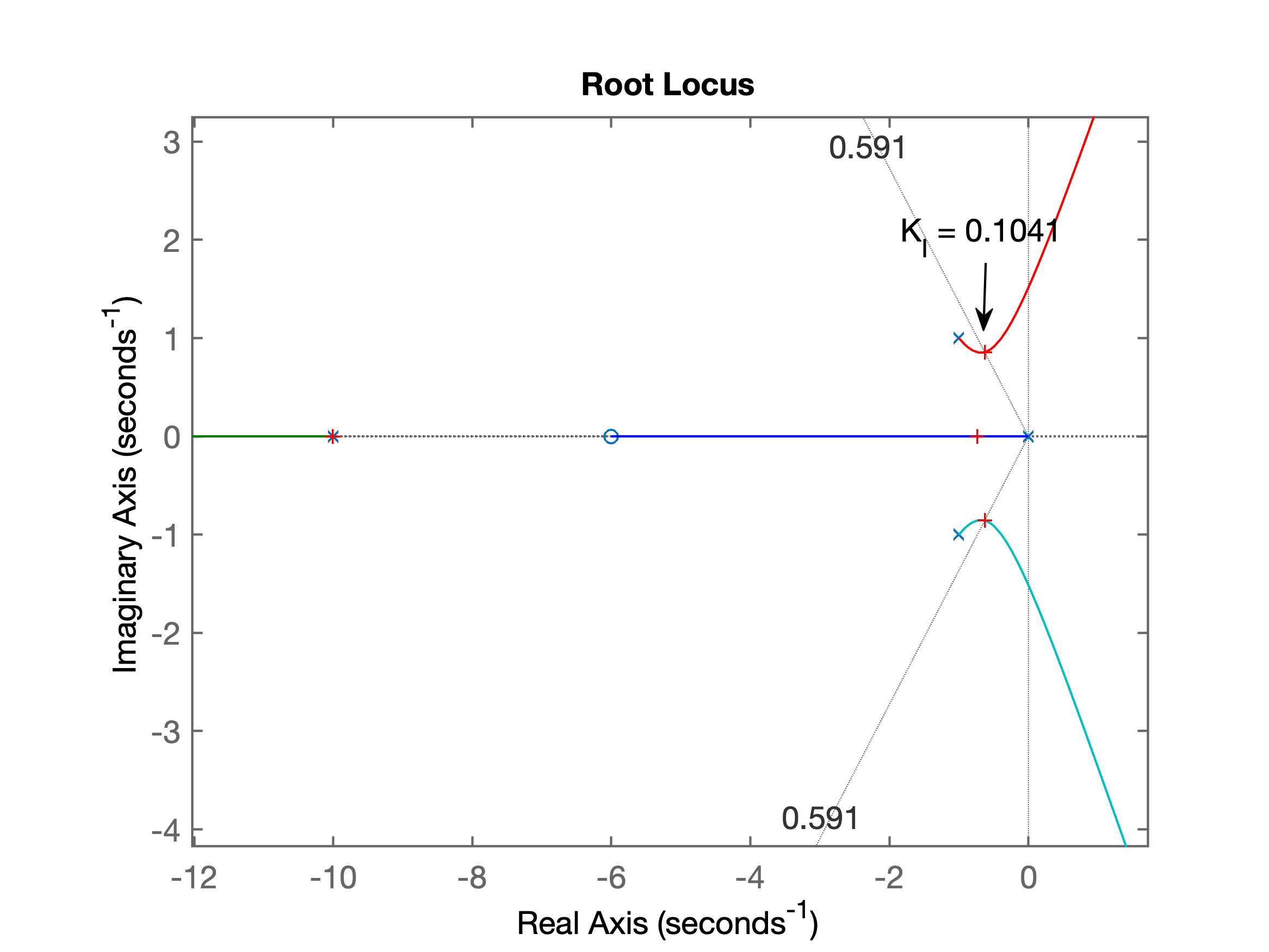
Equação final do controlador:
Incorporando entrada degrau à referência para verificar a resposta temporal obtida com a introdução deste controlador, no Matlab:
xxxxxxxxxx>> ftmf_I=feedback(K_I*ftma_I, 1);>> figure; step(ftmf_I)>> % figura salva como: G1_step_C_I_puro.pngO que gera o gráfico:
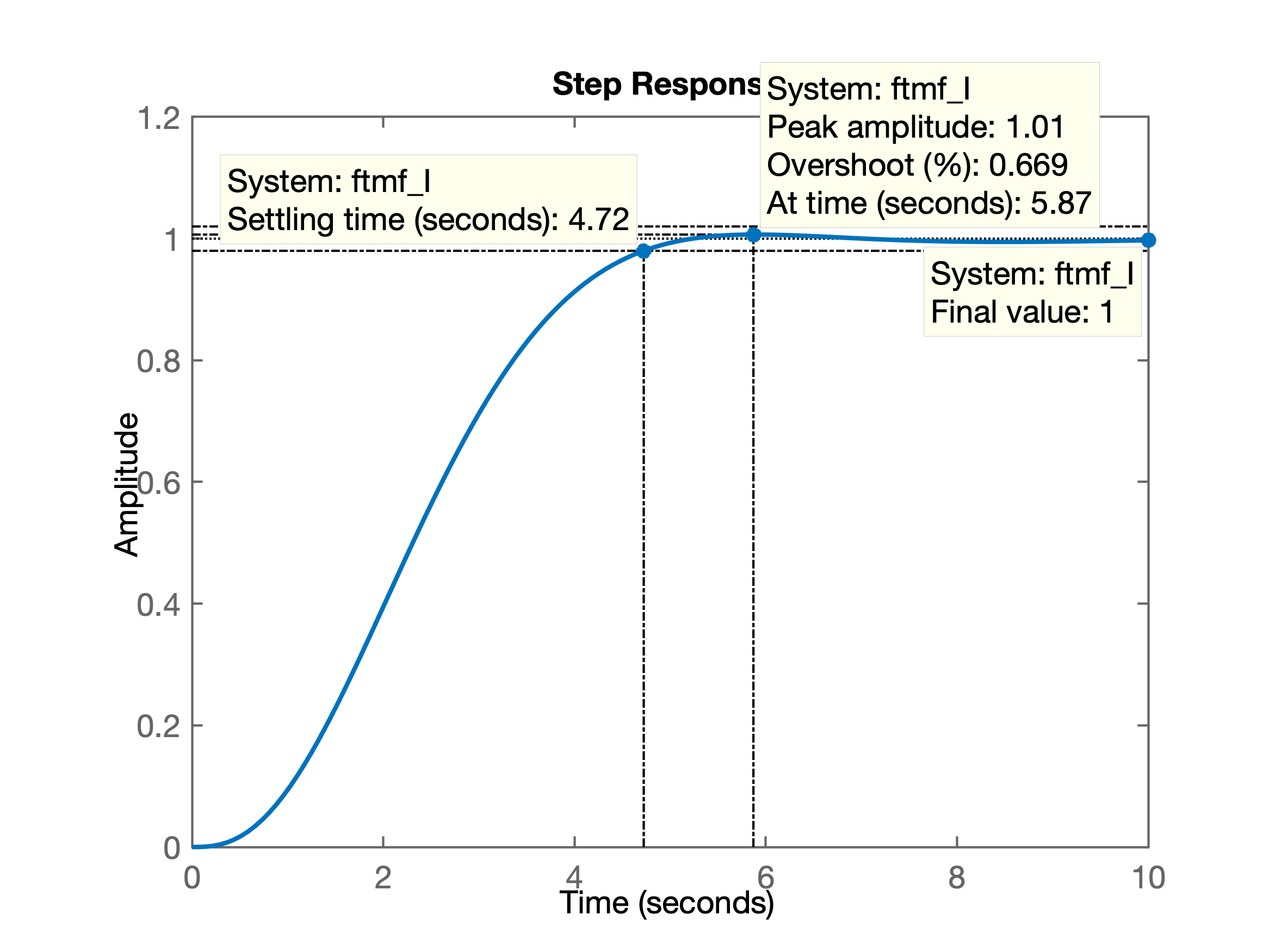
De onde se percebe que poderíamos ter adotado um ganho ainda maior, dado que mau foi produzido um overshoot. O sistema quase resultnum num comportamento super-amortecido.
Analisando o gráfico do RL percebemos algums coisas:
- em malha-fechada (MF), o sistema resultou com 3 pólos dominantes. Repare que além do par de pólos complexos em , também temos a ocorrência de um polo real em , ou seja, este polo real é tão "dominante" na resposta quanto o par de pólos complexos. E por estarem tão próximos, a idéia de aproximar a resposta de um sistema de MF para o de um sistema de 2a-ordem com apenas 1 par de pólos complexos desanda, porque neste caso temos um terceiro pólo real muito próximo do par compleo de pólos. Motivo pelo qual a estimativa inicial dos cálculos para , não se cumprem quando fechamos a malha. Esteja conciente que quanto aproximamos a resposta de um sistema de ordem qualquer para um o de um sistema de 2a-ordem com apenas 1 par de pólos complexos dominantes, nem sempre é isto que acontece, como é o caso aqui.
- Este terceiro pólo real dominante é causado pelo própio pólo do integrador (em ) que está sendo atraído pelo próprio zero da planta. Note:
xxxxxxxxxx>> pole(ftma_I)ans = 0.0000 + 0.0000i -10.0000 + 0.0000i -1.0000 + 1.0000i -1.0000 - 1.0000i>> zero(ftma_I)ans = -6>> Alguém poderia pensar em aumentar o ganho neste momento. Percebe que neste caso em particular, aumentar o ganho implica em 2 consequencias algo contraditórias entre si:
- Num primeiro momento, aumentar o ganho vai fazer com o RL do terceiro pólo dominantes "caminhe" mais rápido da sua posição de origem em para o zero da planta localizado em , porém:
- Não esquecer a resposta deste sistema em malha fechada também estará sendo definida pelo par de pólos complexos, todos muito próximos. Mas ao contário do que acontece com o terceiro pólo real, este par de pólos complexos, a medida que o ganho aumenta, se aproxima cada vez mais do eixo do plano, além de implicar em aumento de overshoot (aumento no valor de ).
Se o aumento de for exagerado, o sistema inclusive deixa de ser estável; os pólos complexos passam a ocorrer no semi-plano direito do plano. Analizando o RL percebemos que se , o sistema em MF ficará instável -- ver próxima figura:
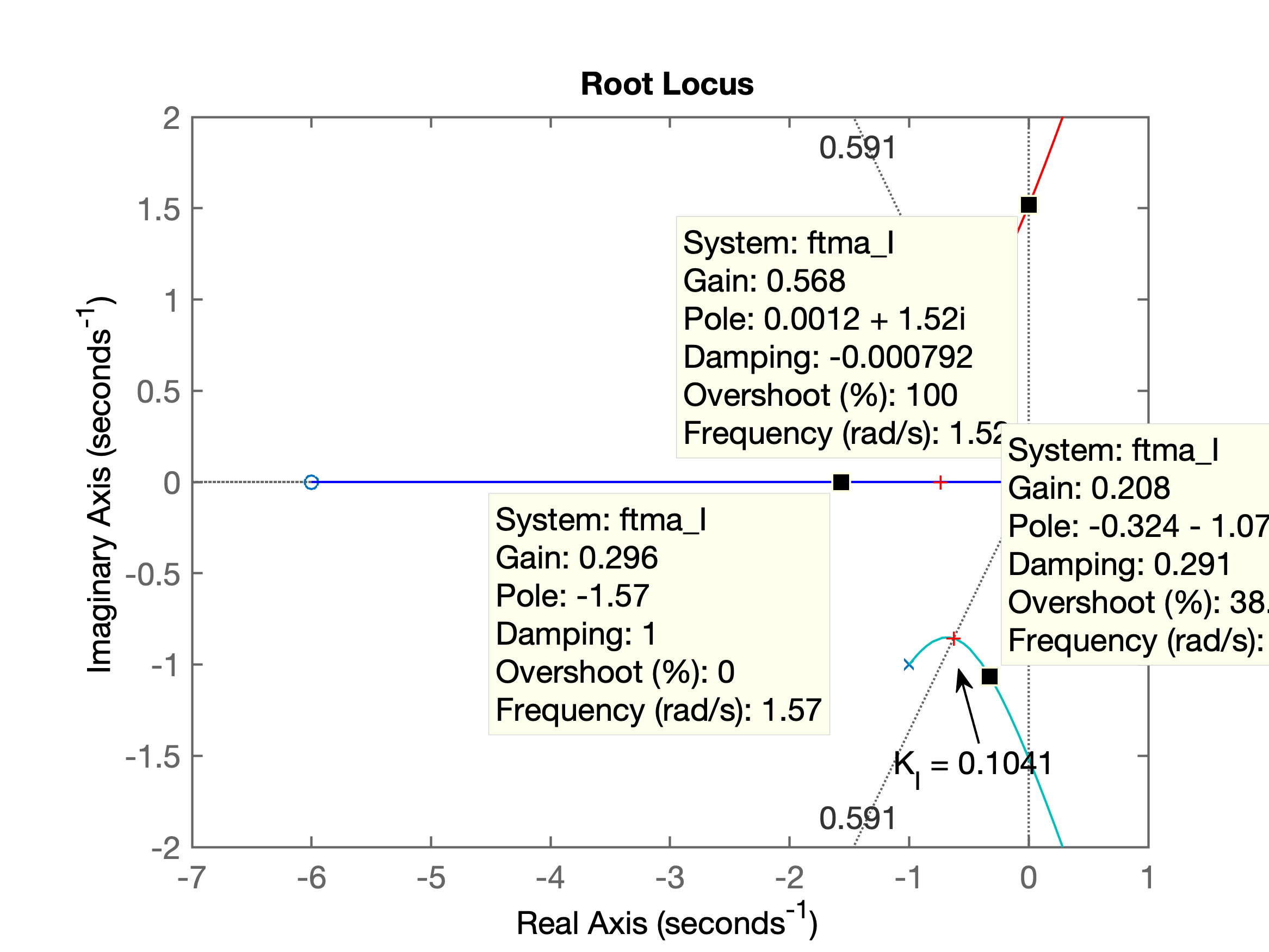
Reparec na figura anterior que com um ganho em torno de , teremos um pólo real localizado em mais rápido que o obtido com o ganho anterior (, pólo real em ), mas o overshoot vai aumentar: o matlab estima o overshoot em e pior, a parte real dos pólos complexos ficarão mais próximo do eixo , especificamente em , tornando a resposta ainda mais lenta que os pólos de MF obtidos com (que ficavam com a parte real em ). De fato, um teste fechando a malha com resulta em:
xxxxxxxxxx>> K_I2=0.290;>> ftmf_I2=feedback(K_I2*ftma_I, 1);>> figure; step(ftmf_I, ftmf_I2)>> legend('Int. Puro (K=0,1041', 'Int. Puro (K=0.290)')Gerando o gráfico à seguir:
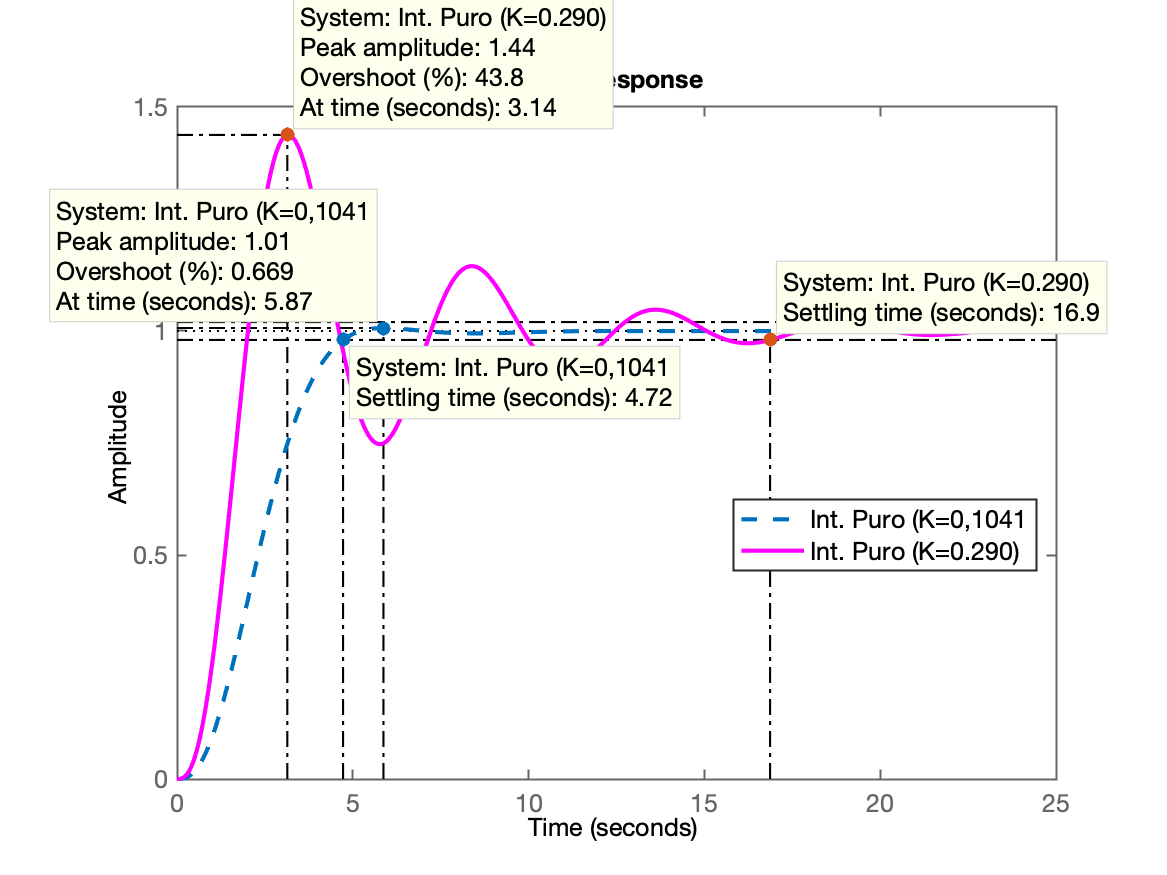
Planta 2
Seja a planta definida pela equação:
Tentar projetar diferentes controladores para atender aos seguintes requisitos de controle:
- segundos;
- ;
- ;
- , mas .
g) Controlador por Avanço-Atraso de Fase (Lead-Lag)
Realizado na aula de 31.10.2019
Resolução iniciada a partir deste ponto...
Entrando com dados da planta:
xxxxxxxxxx>> G2=tf(80, poly([-8 -5 -2]));>> zpk(G2)ans = 80 ----------------- (s+8) (s+5) (s+2) Continuous-time zero/pole/gain model.Procedimento:
- Inicia-se pelo projeto do controlador de Avanço de Fase (Lead) para garantir os requisitos de controle temporais, no caso, tentar atender .
- Depois se parte para o projeto do controlador de Atraso da Fase que visa limimitar o erro de regime permanente ao valor especificado.
O diagrama de blocos referente ao projeto deste controlador fica:
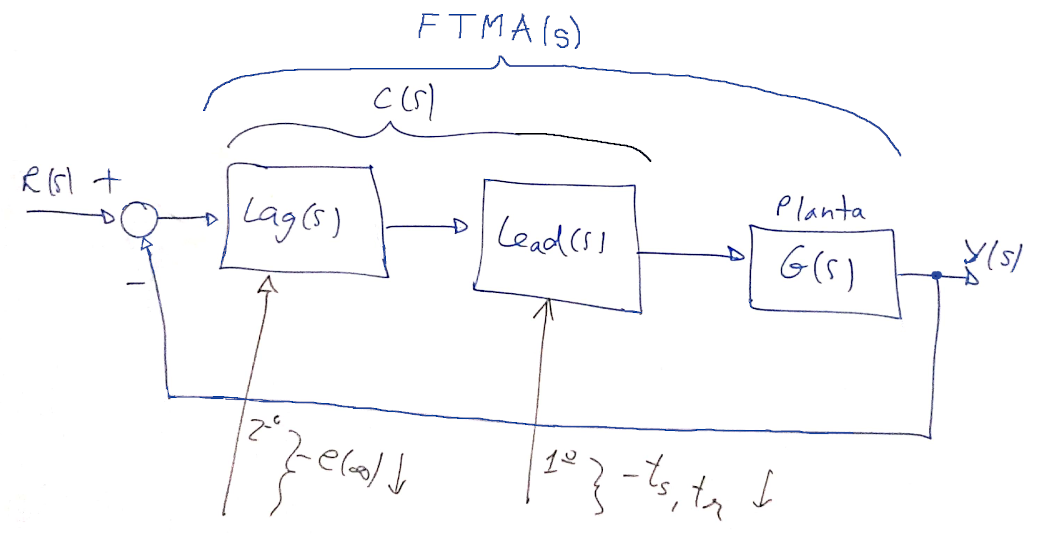
Revisando a estrutura de controladores Lead e Lag temos:
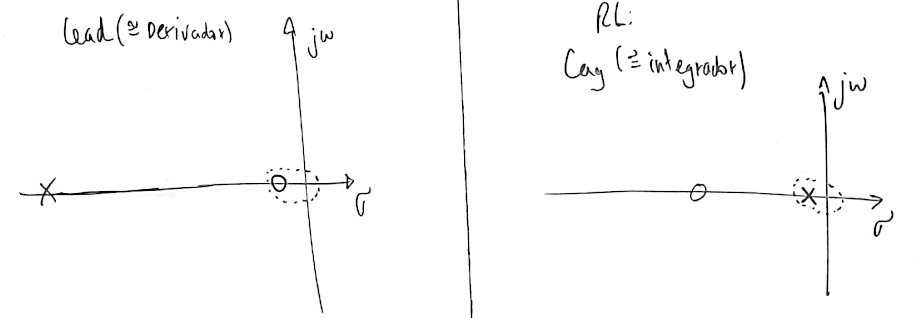
Iniciamos pelo projeto do controlador de Avanço (Lead). Para tanto, temos que analizar o RL para avaliar posições adequadas para seu par pólo-zero.
O zero do controlador Lead deve estar o mais próximo possível da origem do plano-s. Mas devemos lembrar que este zero tentará atrair o pólo mais lento da planta localizado em .
Opções:
- zero entre .
- zero entre
Para os dois casos, o pólo deste controlador fica localizado na direção de . Escolhemos posicionar o mesmo, mais distante (na direção de ) que o pólo mais lento da planta localizado em , posicionando-o em: .
Esboçando os RLs teremos:
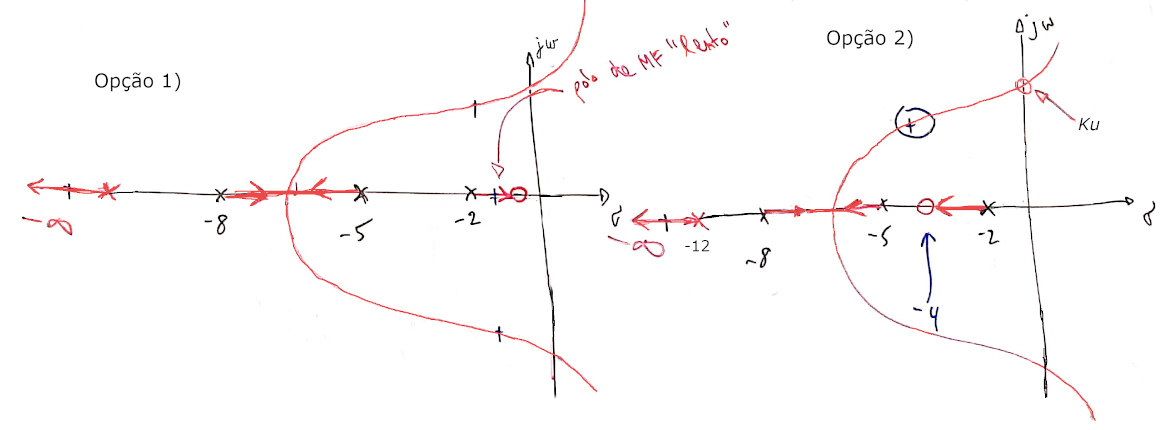
Para a opção 1, a equação do Lead ficaria algo como:
Neste caso, se percebe pelo RL que ocorrerá um pólo real de MF entre -2 à 0 no plano-s, com o pólo real indo na direção da origem do plano-s, ou seja, caracterizando uma resposta temporal bastante lenta.
Para a opção 2, a equação do Lead ficaria algo como:
Nesta opção, ocorrerá um pólo real de MF entre o pólo mais lento da planta (em ) e o zero alocado para o controlador. Neste caso, este pólo se afasta da origem do plano-s e fica mais distante do mesmo, em comparação com a opção 1.
Nos 2 casos, ocorrerão 3 pólos dominantes (mais próximos da origem do plano-s): um par conjugado complexo que caracteriza respostas típicas de sistemas de 2a-ordem com e um pólo real que irá distorcer a resposta temporal esperada para o par de pólos complexos.
Seguindo com a opção 2 para o controlador Lead, teremos:
xxxxxxxxxx>> % opção 2...>> G_lead=tf([1 4],[1 12]);>> ftma_lead=G_lead*G2;>> rlocus(ftma_lead)O último comando gera o RL, mas vamos aproveitar e incluir onde deveriam estar os pólos de MF para cumprir com os requisitos de controle especificados para esta planta:
xxxxxxxxxx>> % calculando posição desejada para os pólos de MF>> OS=20; % overshoot máximo especificado>> ts=1.1; % tempo máximo de assentamento especificado>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))zeta = 0.4559>> wn=4/(zeta*ts)wn = 7.9754>> wd=wn*sqrt(1-zeta^2)wd = 7.0981>> % wd = parte imaginária dos pólos de MF>> sigma = wn*zeta % calculando parte real dos pólos de MFsigma = 3.6364>> % montando vetor dos pólos de MF>> polos_mf=[-sigma+i*wd -sigma-i*wd]polos_mf = -3.6364 + 7.0981i -3.6364 - 7.0981i>> figure(1) % foco no RL anterior>> hold on % comando para sobrepor gráfico dos pólos de MF>> % desejados sobre o RL anterior>> plot(polos_mf,'r+')>> sgrid(zeta,wn) % Aproveitando para sobrepor linhas guias do zeta e wnPodemos agora definir um ganho para este controlador com o objetivo de testar se esta proposta permite atender aos requisitos temporais desejados:
xxxxxxxxxx>> [K_Lead,aux]=rlocfind(ftma_lead) % encontrando o valor do ganho do LeadSelect a point in the graphics windowselected_point = -3.3842 + 6.6729iK_Lead = 7.7172aux = -16.9761 + 0.0000i -3.0687 + 6.5241i -3.0687 - 6.5241i -3.8864 + 0.0000i>> % testando o lead...>> ftmf_lead=feedback(K_Lead*ftma_lead, 1); % fechando a malha com o Lead>> figure; step(ftmf_lead) % verificando resposta>> % alguns valores encontrados:>> % ts=1,22; %OS=19.3%>> % calculando erro em regime permanente do Lead>> (1-dcgain(ftmf_lead)/1)*100ans = 27.9925>> % Ou seja, quase 28% de erro, tudo bem porque o controlador Lag vai corrigir este erro.A figura à seguir confirma o RL e mostra o ganho adotado inicialmente:
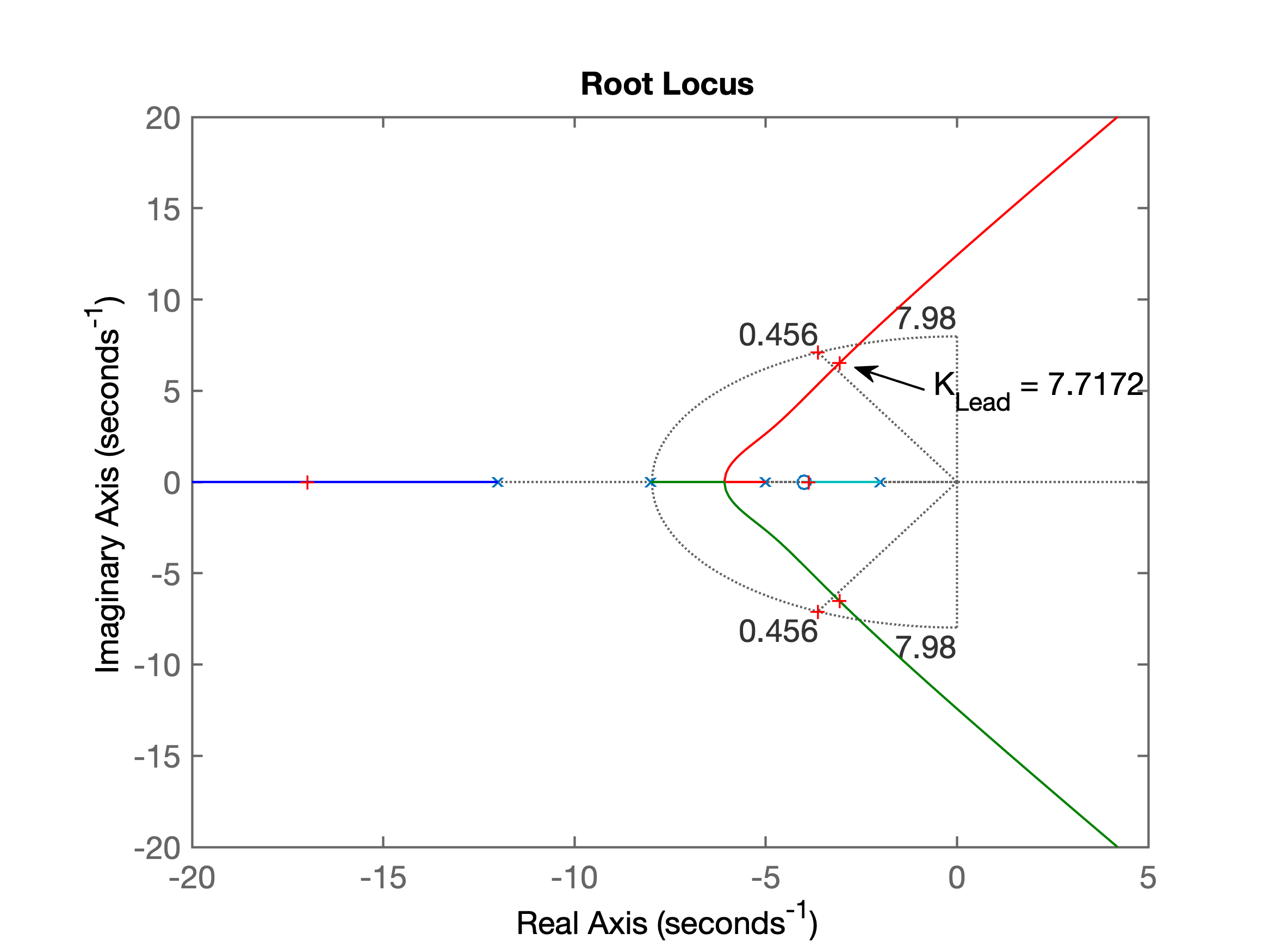
E a seguinte resposta ao degrau é encontrada:
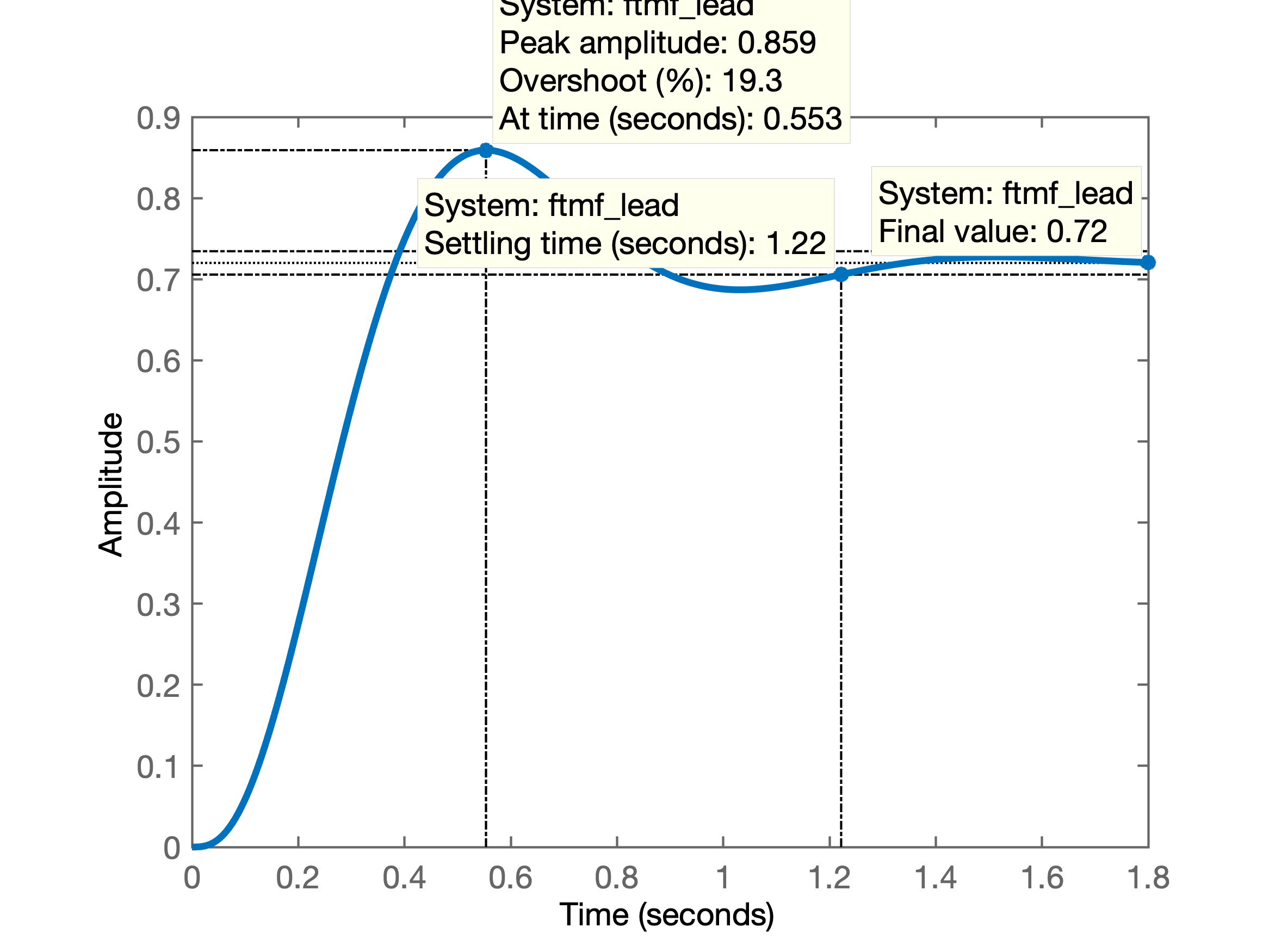
Porém, reparando no RL gerado, percebemos que provavelmente adotar um ganho mais baixo para o Lead, vai permitir afastar mais os pólos complexos conjugados do eixo , apesar de repercutir num erro maior em regime permanente (e também num menor.) A questão do erro será corrigida com a introdução do controlador Lag:
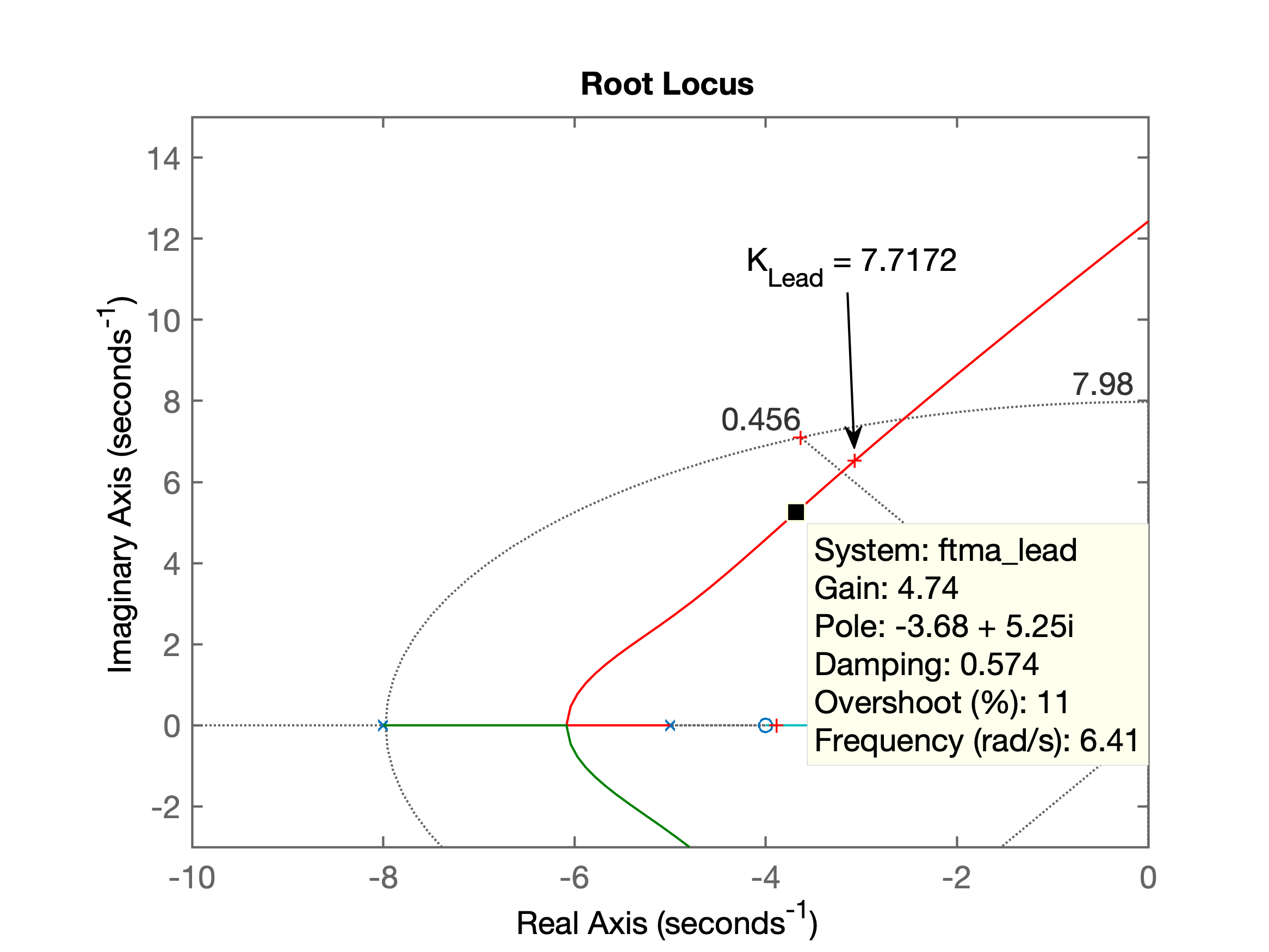
Optando por reduzir o ganho do controlador Lead para , teremos:
xxxxxxxxxx>> K_Lead=5;>> % testando em quanto ficou ts com este ganho>> ftmf_lead=feedback(K_Lead*ftma_lead, 1);>> figure; step(ftmf_lead)>> % com este valor de ganho:>> % ts(Lead)=0,964; y(\infty)=0,625 -- isto é, o erro aumentou>> (1-dcgain(ftmf_lead))/1*100ans = 37.5000>> % Se espera compensar o aumento do erro, com o controlador Lag.Segue abaixo a nova resposta temporal encontrada:
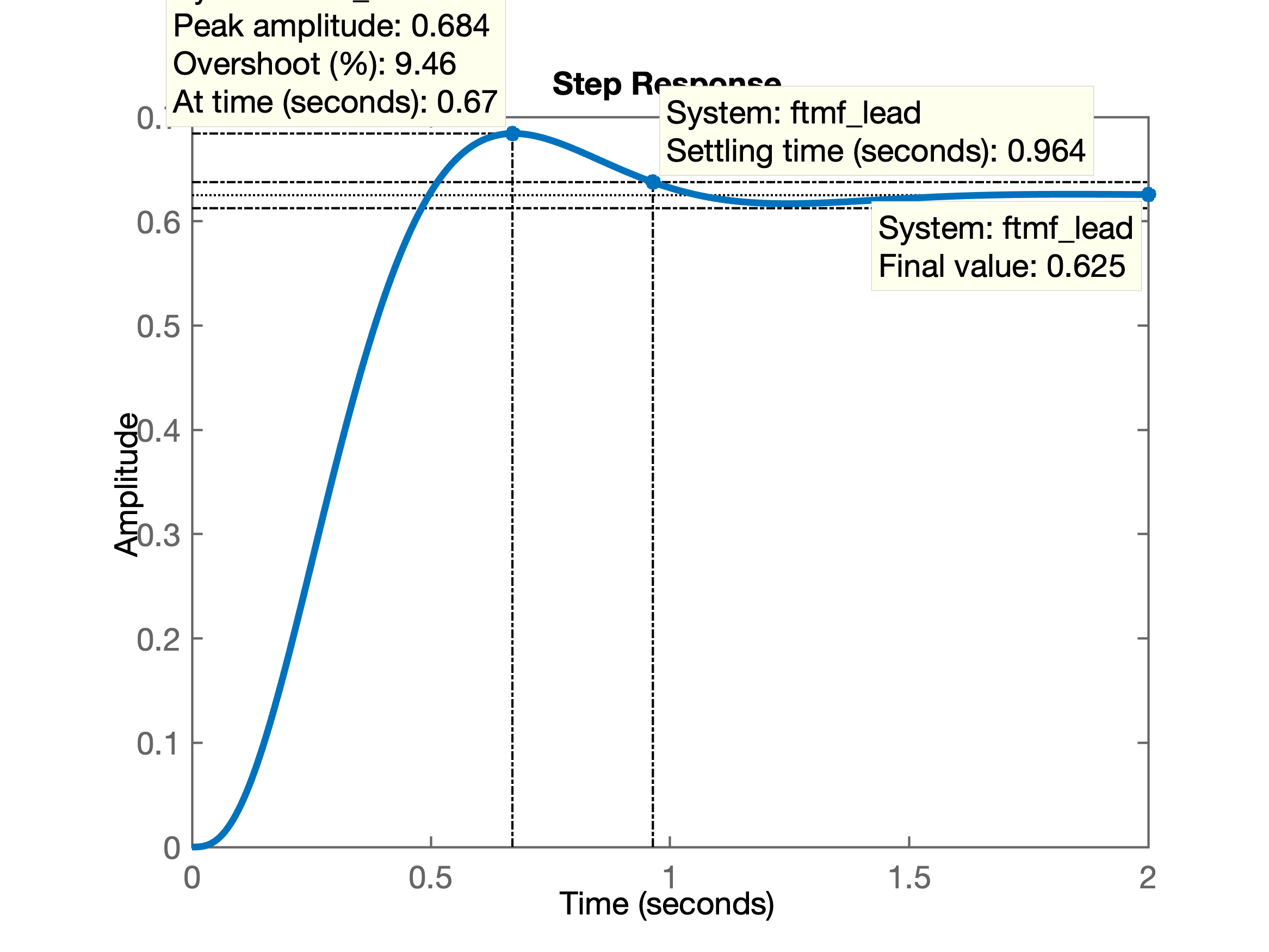
Continuando com o projeto do controlador Lag...
Temos que analizar agora opções para introdução do par pólo-zero do controlador Lag. O objetivo pretendido com a inclusão deste controlador é reduzir o erro em regime permanente. Para tanto, convêm aproximar seu pólo o máximo possível da origem do plano-s.
Analizando opções possíveis no RL, temos:
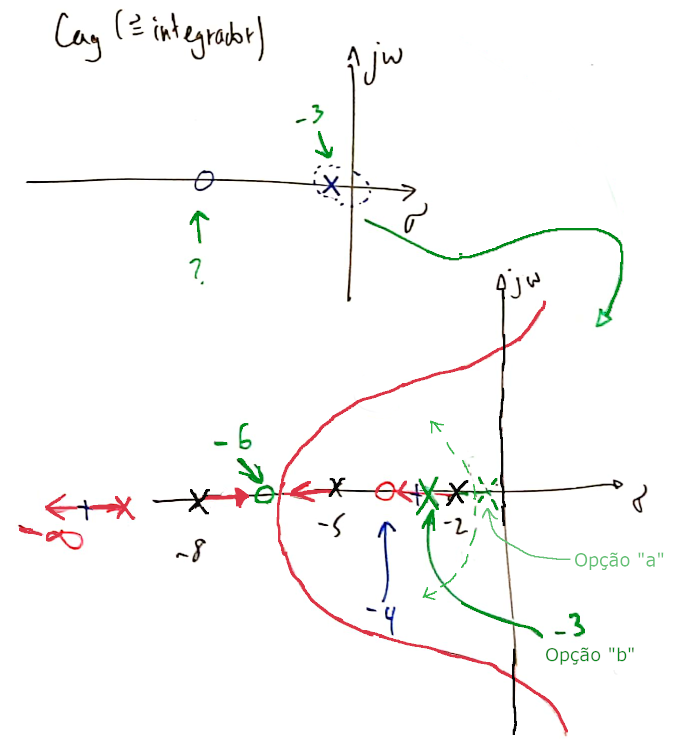
A opção "a": nesta proposta o pólo do controlador ficaria entre , resultando num RL com ponto de partida ("break-out") entre o pólo mais lento da planta (em ) e o pólo do controlador Lag. Isto resultará pólos de MF complexos lentos.
A opção "b": neste caso, o pólo do controlador ficaria entre (em está o zero do controlador Lead). Esta proposta parece mais promissora porque o RL resultará num ponto de partida que deve ocorrer entre o pólo mais lento da planta (em ) e o pólo do controlador (Lag) que neste caso, estaria mais afastado do eixo , propiciando uma resposta temporal mais rápida à despeito de uma menor redução no erro em regime permanente que o pretendido.
Efetivando os cálculos no Matlab para avaliar a proposta:
xxxxxxxxxx>> % Definindo o Lag>> C_Lag=tf([1 6],[1 3])C_Lag = s + 6 ----- s + 3 Continuous-time transfer function.>> ftma_lead_lag=C_Lag*G_lead*G2;>> % RL final>> figure; rlocus(ftma_lead_lag)>> hold on>> plot(polos_mf,'m+') % plota os pólos de MF desejados em magentaO RL resultante aparece na figura abaixo:
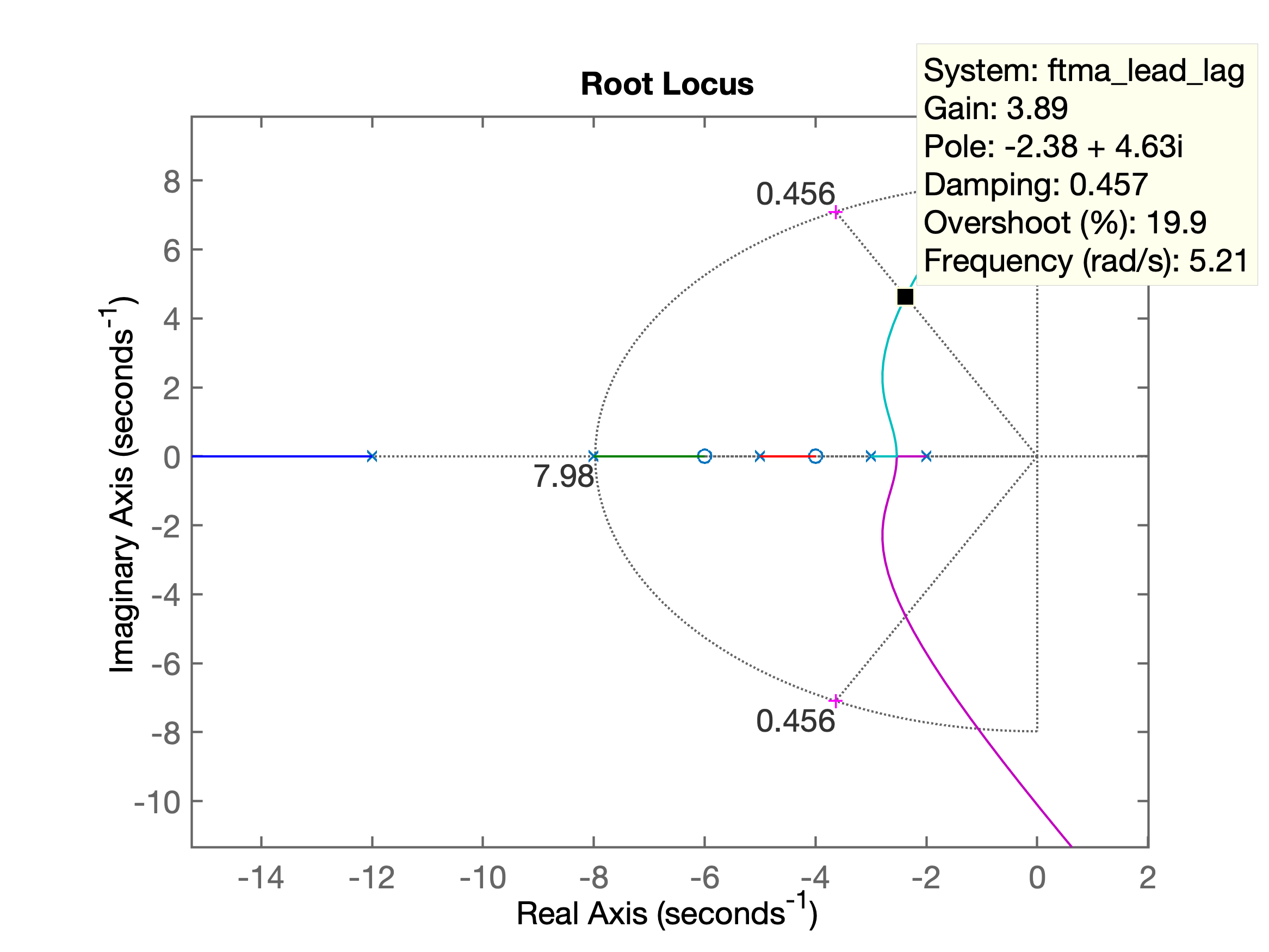
Analisado o RL anterior se percebe que a proposta não permitiu definir um RL que passe próximo dos pontos desejados para os pólos de MF. Eventualmente deslocar o zero do controlador Lag para um ponto mais distante que na direção para , possa melhorar o RL. Avaliando...
xxxxxxxxxx>> % Realizando um ajuste no Lag...>> C_Lag=tf([1 10],[1 3]) % afastando o zero do Lag...C_Lag = s + 10 ------ s + 3 Continuous-time transfer function.>> ftma_lead_lag=C_Lag*G_lead*G2;>> % verificando como ficou o RL...>> figure; rlocus(ftma_lead_lag)>> hold on;>> plot(polos_mf,'m+')>> sgrid(zeta,wn)>> sgrid(zeta,wn)Este ajuste causou pouco impacto no RL, conforme pode ser visto na próxima figura:
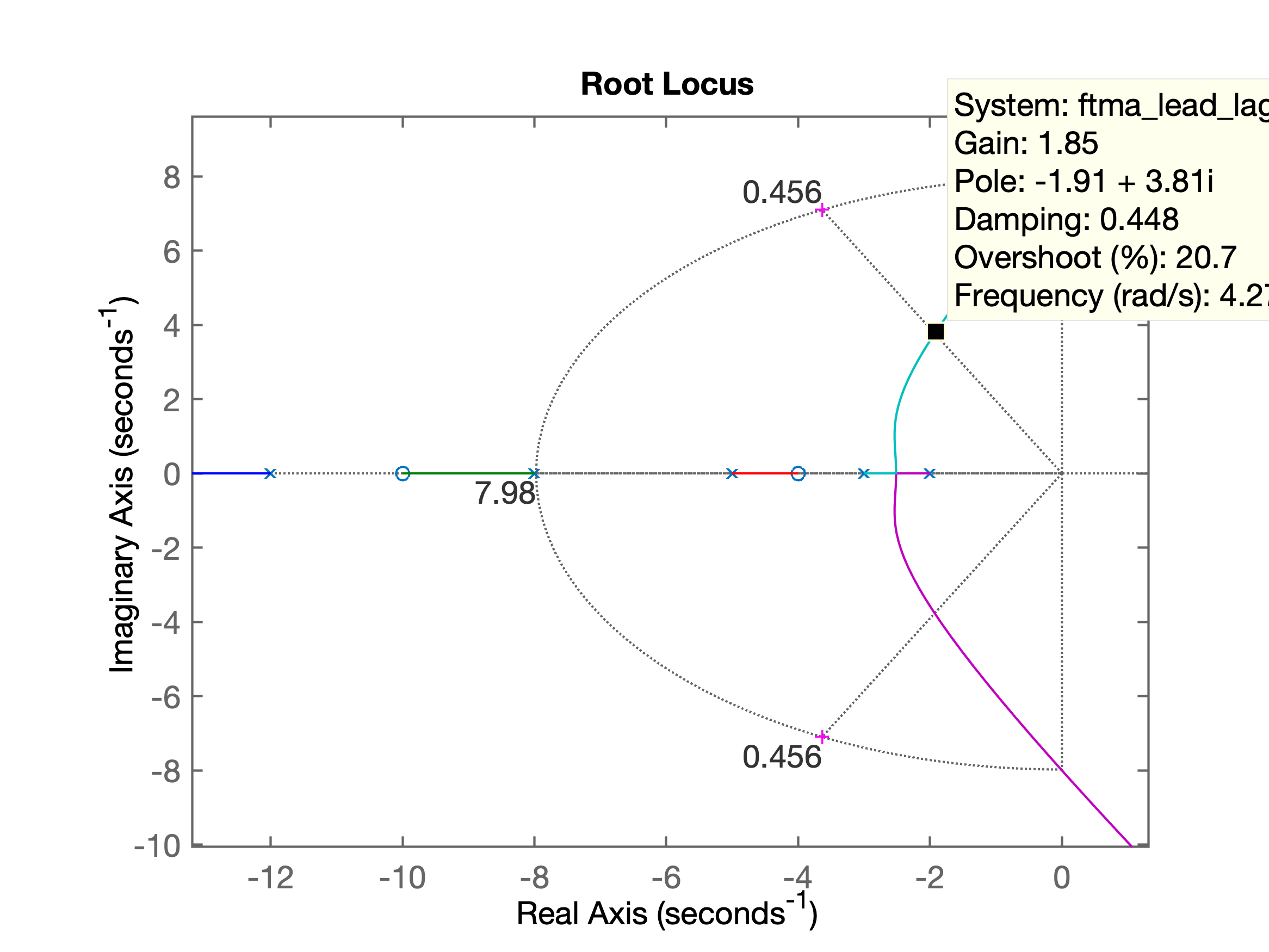
Este último RL já aponta (Data cursor) o local escolhido para o ganho de malha fechada do controlador Lead-Lag: . Fechando a malha com este ganho:
xxxxxxxxxx>> K_lead_lag=1.85;>> ftmf_lead_lag=feedback(K_lead_lag*ftma_lead_lag, 1);>> figure;>> step(ftmf_lead_lag)>> erro=(1-dcgain(ftmf_lead_lag))/1*100erro = 32.727>> diary offObtendo o resultado:
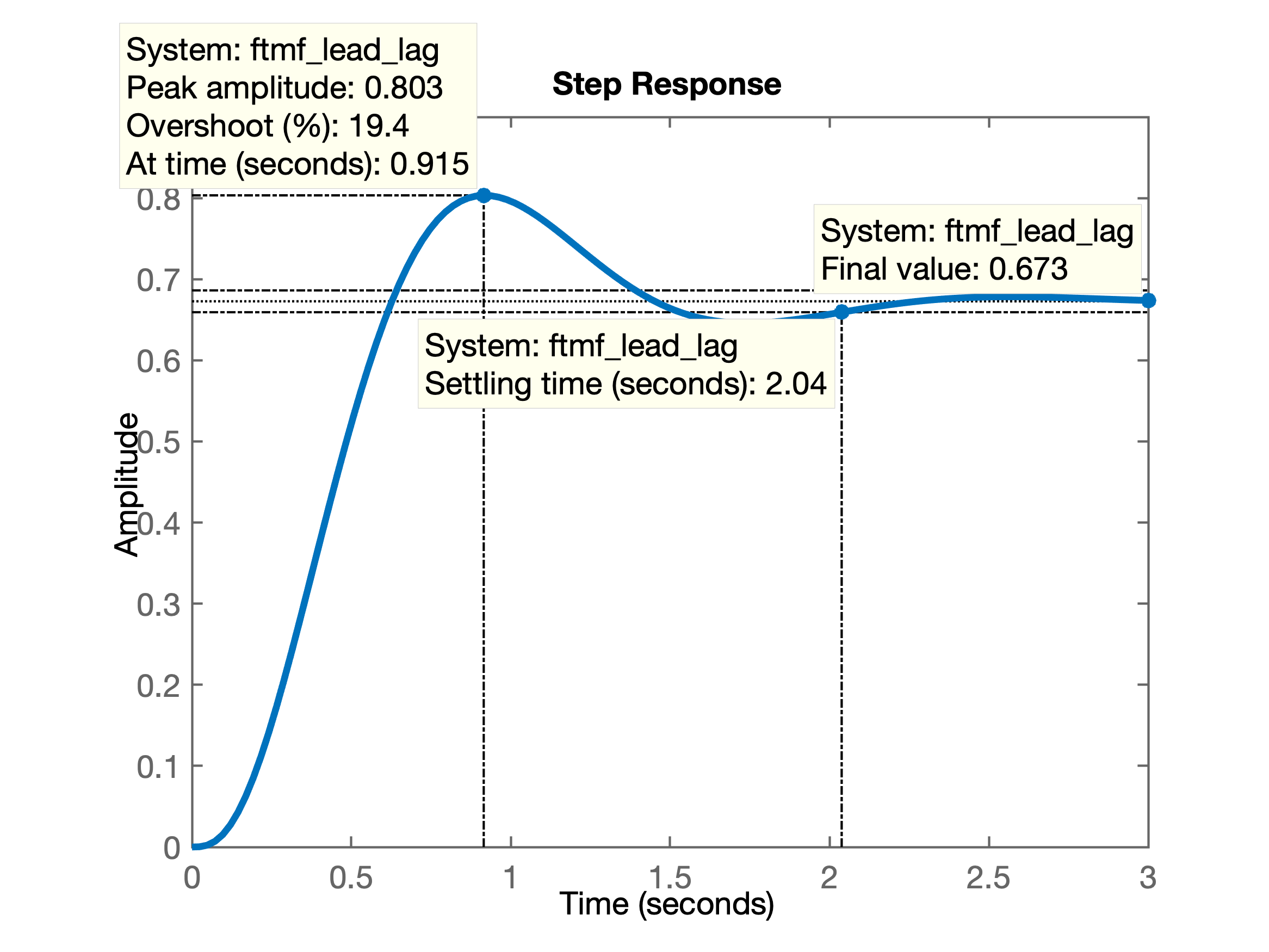
Onde podemos observar os seguintes resutlados:
- (desejado )
- (desejado )
Estes resultados foram obtidos com o seguinte controlador:
Analisando o RL anterior, percebemos que eventualmente alguns ajustes podem melhorar o desempenho deste controlador:
- O pólo do controlador Lag poderia até permanecer em (apesar de provavelmente não contribuir muito para redução do ).
- O zero do controlador Lead (em ) poderia ser deslocado mais para . Este zero atraí o 2o-pólo mais lento da planta localizado em , fazendo como que este RL caminhe na direção do eixo , quando o contrário (RL "caminhando" para a direção de seria o desejado). Isto pode ser ajustado, modificando a posição do zero do Lead de para por exemplo.
Teríamos então:
Testando...
xxxxxxxxxx>> C_lead_lag2=tf(poly([-6 -2.2]),poly([-12 -10]));>> zpk(C_lead_lag2)ans = (s+6) (s+2.2) ------------- (s+12) (s+10) Continuous-time zero/pole/gain model.>> ftma_lead_lag2=C_lead_lag2*G2;>> figure; rlocus(ftma_lead_lag2);>> hold on;>> plot(polos_mf,'m+')>> sgrid(zeta,wn)>> axis([-15 2 -10 10]) % realizando "zoom" na região de interesse>> [K_lead_lag2,aux]=rlocfind(ftma_lead_lag2) % encontrando o ganhoSelect a point in the graphics windowselected_point = -4.6570 + 8.1860iK_lead_lag2 = 11.8172aux = -19.6899 + 0.0000i -4.6078 + 8.1588i -4.6078 - 8.1588i -5.9469 + 0.0000i -2.1476 + 0.0000i>> % o ganho (mais elevado) foi colocado no prolongamento da linha guia>> % correspondente ao zeta desejado - ganho maior: menor erro>> % fechando a malha>> ftmf_lead_lag2=feedback(K_lead_lag2*ftma_lead_lag2, 1);>> figure; step(ftmf_lead_lag2);>> erro=(1-dcgain(ftmf_lead_lag2))/1*100erro = 43.4803>> save planta2Resulta o seguinte RL (bastante mais promissor):
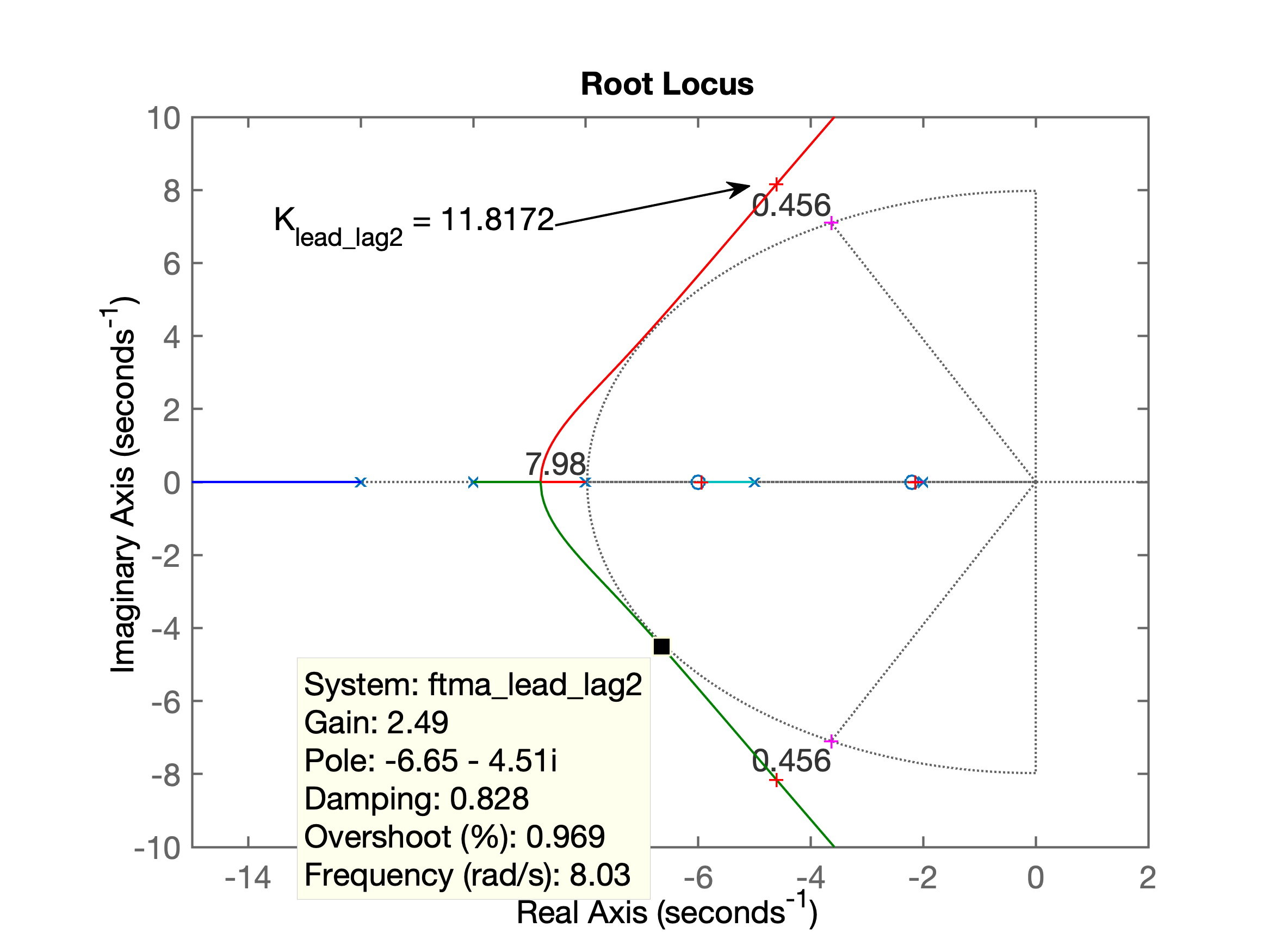
E a seguinte resposta ao degrau:
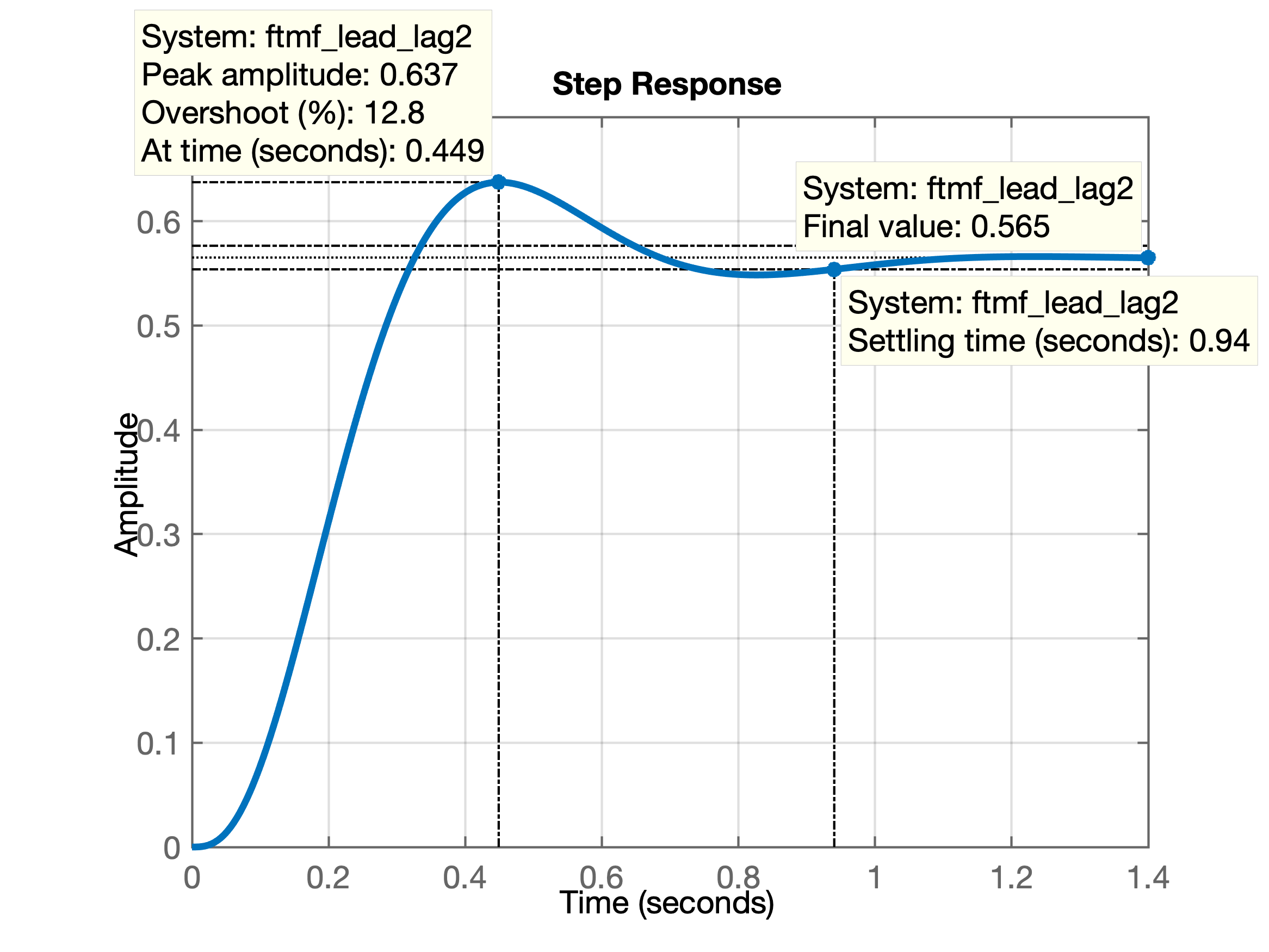
Infelizmente percebemos que não foi possível reduzir o erro para . Muito provavelmente porque o pólo do controlador Lag deveria estar mais próximo do eixo para compensar o erro provocado pelo controlador Lead. Mas esta alteração implica em todo um novo estudo. E eventualmente só com introdução de ação integral (PID) se consiga atingir mais facilmente os requisitos de controle especficados para esta planta.
Planta 3
Seja a planta definida pela equação:
Tentar projetar diferentes controladores para atender aos seguintes requisitos de controle:
- segundos;
- ;
- ;
- , mas .
a) Controlador Proporcional
b) Contrale por Ação Integral Pura
c) Controlador PI
d) Controlador por Atraso de Transporte (Lag)
e) Controlador PD
f) Controlador por Avanço de Fase (Lead)
g) Controlador por Avanço-Atraso de Fase (Lead-Lag)
Prof. Fernando Passold