Projeto de Controladores usando RL

Obs.: Início das aulas associado com projeto de controladores usando ferramente do Lugar Geomátrico das Raízes, ou mais simplesmente, “root locus” — Aula do dia 10/10/2020 (Eng. Computação).

Ingressando a Planta

Seja a planta, $G(s)$:

No Matlab:

>> G=tf(1, poly( [ -1    -2 10 ] ) )

G =

             1
  -----------------------
  s^3 - 7 s^2 - 28 s - 20

Continuous-time transfer function.

>> % Verificando...
>> zpk(G)

ans =

          1
  ------------------
  (s-10) (s+2) (s+1)

Continuous-time zero/pole/gain model.

Ops, nota-se que o pólo que deveria estar em $s=-10$ foi ingressado de maneira incorreta. Repetindo-se o comando >> G=tf(..):

>> G=tf(1, poly( [ -1 -2 -10 ] ) )

G =

             1
  ------------------------
  s^3 + 13 s^2 + 32 s + 20

Continuous-time transfer function.

>> zpk(G)

ans =

          1
  ------------------
  (s+10) (s+2) (s+1)

Continuous-time zero/pole/gain model.

Projeto de Controlador Proporcional

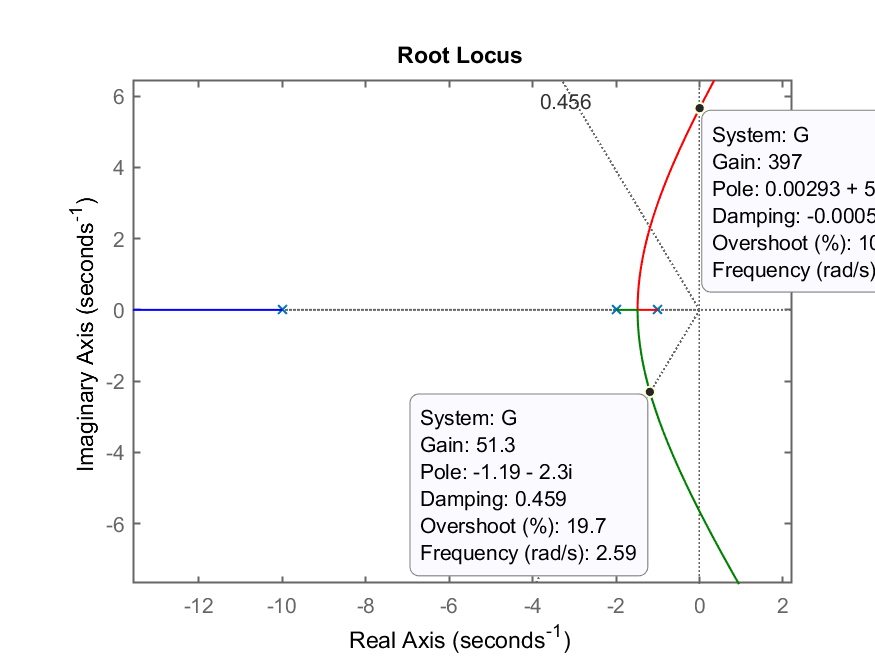
Usando Root-Locus, projetar umn controlador Proporcional. Este controlador têm como único requisito de controle, que o overshoot (sobre-sinal) em MF não seja superior à 20%.

Usando-se o Matlab:

>> rlocus(G)
>> % Calculando zeta correspondendo a este %OS
>> OS=20; % 20% de overshoot tolerável
>> zeta=(-log(OS/100))/(sqrt(pi^2+(log(OS/100)^2)))
zeta =
      0.45595
>> hold on
>> sgrid(zeta,0);

Gráfico do RL ressaltando alguns valores de ganho:

Adotaremos o ganho de $K=51$.

Verificando o resultado obtido…

>> K=51;
>> ftmf=feedback(K*G, 1);
>> figure; step(ftmf);

Obtemos como resultado:

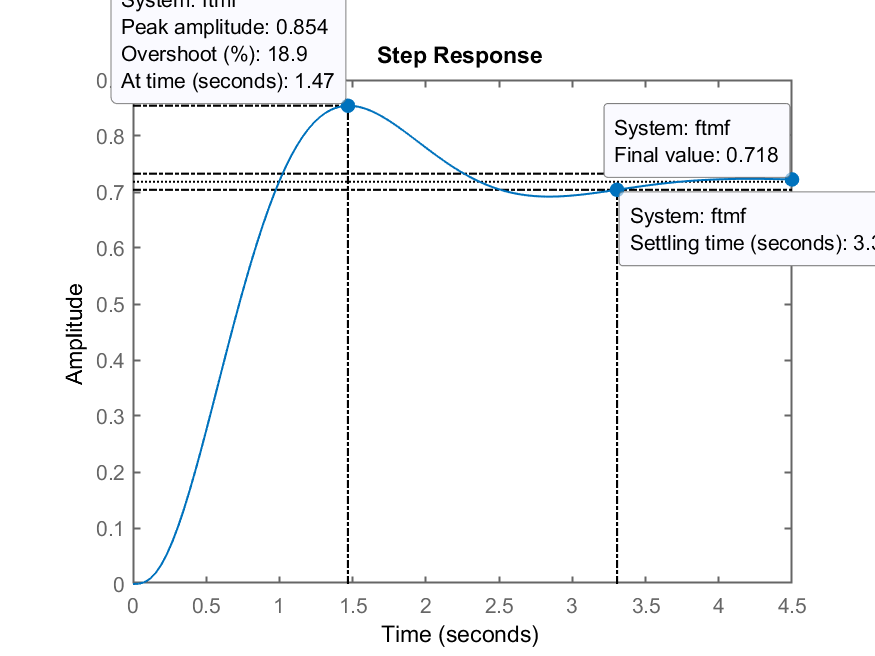
Notamos erro não nulo em regime permanente: $y(\infty)=0,718$. Deveria ter alcançado a amplitude da referência: degrau unitário: $r(\infty)=1,0$. Calculando-se o erro:

>> % Calculando o erro em regime permanente
>> dcgain(ftmf)
ans =
      0.71831
>> erro=(1-dcgain(ftmf))/1*100
erro =
       28.169

Ou seja, acabamos com um erro de regime permanente de $e(\infty)=28,169\%$.

• Esse valor de erro pode ser reduzido?

Resposta: Aumentando-se o ganho, o erro vai ser reduzido mas deve aumentar $\%OS$. Testando…

>> K=75;
>> ftmf=feedback(K*G, 1);
>> figure; step(ftmf);

Resultado obtido com $K=75$:

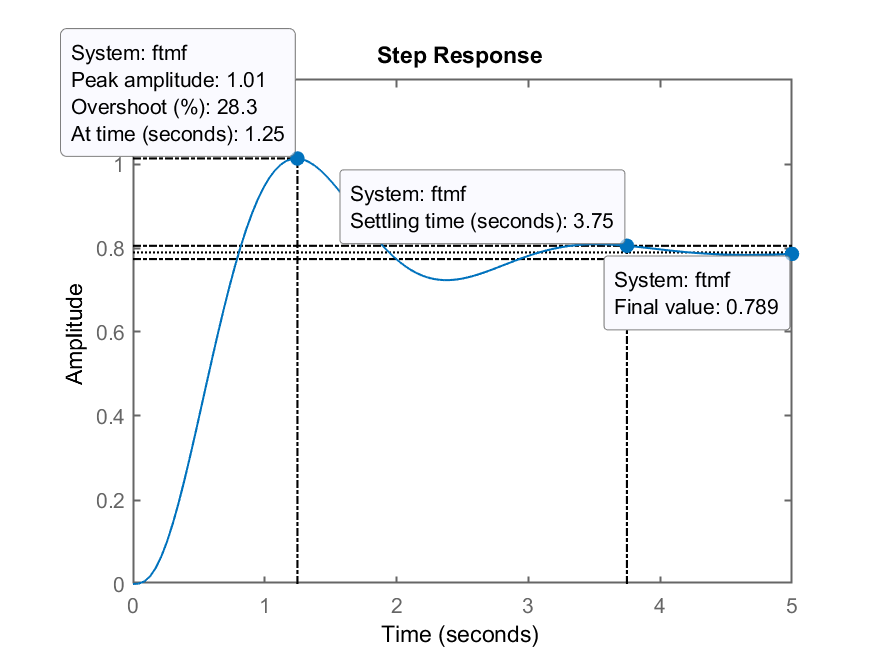
Nota-se uma pequena redução no erro. Poderia-se ter usado uma valor de ganho maior, deste que ficasse abaixo de $K_u \cong 397$ (Ultimate Gain = máximo ganho, que coloca o sistema no limiar na estabilidade, no modo ‘’oscilatório”).

Se fosse usado $K=100$, teríamos obtido:

Perceba que o valor de Overshoot determinado pelo Matlab e mostrado na figura possui relação com o valor em regime permanente da planta, que, com este ganho atingiu: $y(\infty)=0,833$. Quando se especifica overshoot como um requisito de controle, seu valor é em comparação ao valor em regime permamente que a saída da planta deveria atingir (o valor final da referênica). Do ponto de vista de requisitos de controle o overshoot aqui foi de 14% (note no “datatip” da figura: “Peak Maplitude: 1.14”). Ainda estamos abaixo dos 20% máximos especificados para este caso. De todos os modos, mesmo aumentando-se o ganho para $K=100$ ainda estamos com um erro considerável:

>> erro=(1-dcgain(ftmf))/1*100
erro =
       16.7

Definindo o ganho em função do erro em regime permanente…

Lembrando da teoria do erro:

Esta planta é um sistema tipo 0 (sem integrador), então:

Suponha que o erro máximo de regume permanente tenha sido especificado em 10%, então $e(\infty)=10\%=0,1$ e podemos fazer:

Isolando o $K_p$ (ganho estático de posição desejado) obtemos:

No Matlab:

>> Kp=(1-0.1)/0.1
Kp =
      9

Calculando-se agora o: $\lim_{s \to 0} FTMA(s)$:

Por fim, como $K_p=\lim_{s \to 0} FTMA(s)$:

Usando o Matlab:

>> K1=Kp*20
K1 =
   180

Descobrimos que deveríamos ter adotado $K=180$ para $e_{step}(\infty)=10\%$.

Obs.: foi criada a nova variável K1 para guardar este novo valor de ganho e assim se preservar o valor adotado inicialmente para este controlador (variável K).

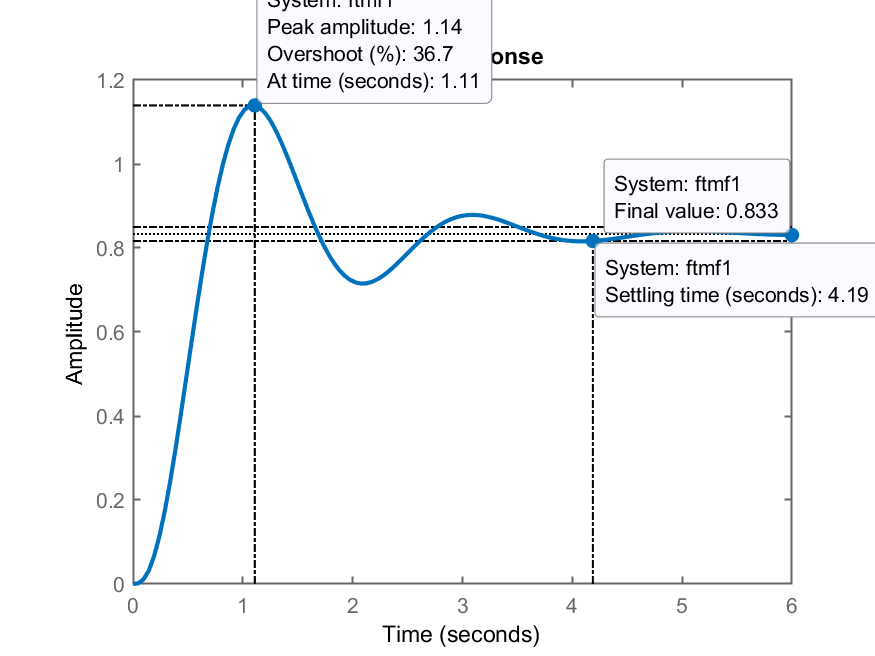
Testando o sistema em MF com $K=180$:

>> ftmf_K1=feedback(K1*G,1);
>> figure; step(ftmf_K1);
>> grid

Obtemos a figura:

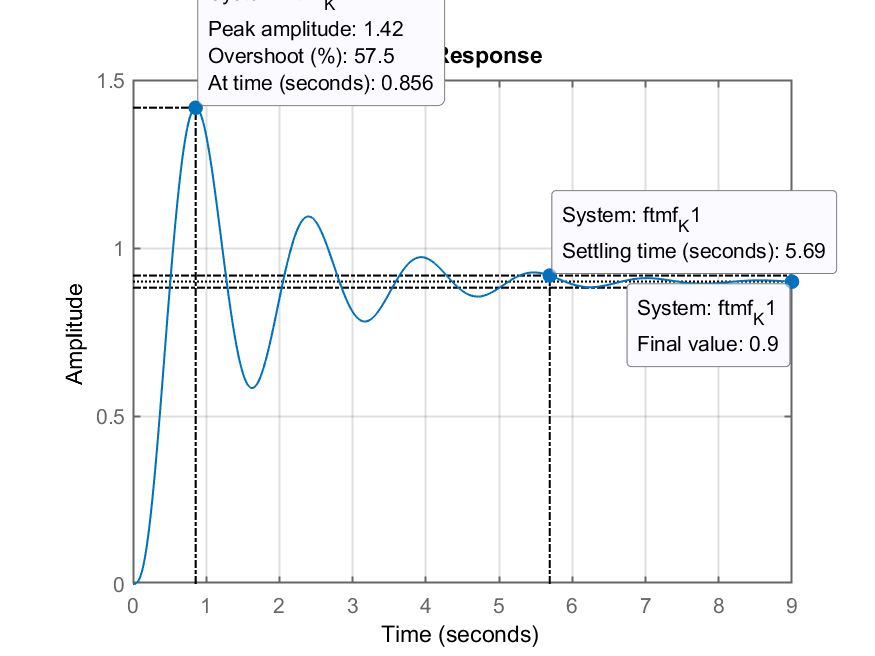
Nota-se que o erro fica limitado exatamente aos 10%, mas às custas de um overshoot bastante expressivo, $\%OS=57,5\%$ em relaçâo ao valor final atingido pela planta ($y(\infty)=0,9$), mas em relação ao valor final desejado, o overshoot ficou em 42%, muito acima dos 20% especificados:

>> OS_calc=(1.42-1)/1*100
OS_calc =
           42

Conclusão: com um controlador proporcional, para esta planta, ou se mantêm erro máximo em 10% ou se limita o overshoot aos 20%. Não há como atender simultaneamente estes 2 requisitos de controle ($erro(\infty) \le 10\%$ e $\%OS \le 20\%$). Se os 2 requisitos devem ser atendidos, outro tipo de controlador deve ser implementado, neste caso, algum contendo pólo ou pólos + zeros.

Para a próxima aula está previsto a inclusão de um controlador com ação integral:

• Controlador Integral Puro;
• Controlador PI (Proporcional + Integral);
• Conotroladorpor Atraso de Fase (similar a um PI).

Obs.: Ao encerrar a seção de trabalho no Matlab, não esquecer de fazer:

>> save dados
>> diary off
>> quit

Na próxima aula recuperaremos os dados (variáveis) já criadas nesta aula, usando o comando >> load dados. Uma cópia de dados.mat pode ser obtido [aqui]. O arquivo aula_10102022.md originalmente usado para criar este documento pode ser encontrado compactado com as figuras geradas durante esta aula, aqui: aula_10102022.zip.