Controle de Velocidade de Motor CC
Artigo original: DC Motor Speed: Simulink Modeling, Control Tutorials for Matlab & Simulink, URL: http://ctms.engin.umich.edu/CTMS/index.php?example=MotorSpeed§ion=SimulinkModeling (acessado em 30/09/2020).
Controle de Velocidade de Motor CCModelagem de Motor CCEquaçõesModelo no SimulinkTeste do ModeloExemplos de Ações de Controle em Velocidade de Motor CC1. Controlador Proporcional2. Controle PI3. Controle PD4. Controle PIDConclusão final
Modelagem de Motor CC
Um atuador bastante comum em sistemas de controle é o motor CC (corrente Contínua). A velocidade do mesmo pode ser variada, variando-se sua tensão de alimentação. Ele fornece movimento rotativo diretamente e também pode fornecer movimento linear usando-se mecanismo de fuso (ou trosca trapezoidal):
| Exemplo 1 | Exemplo 2 | Exemplo 3 | Exemplo 4 | Exemplo 5 |
|---|---|---|---|---|
 |  |  | 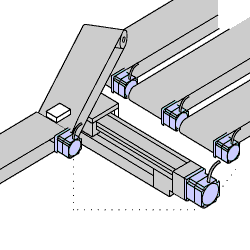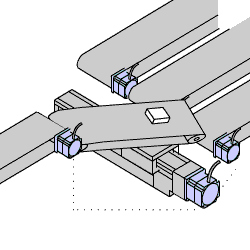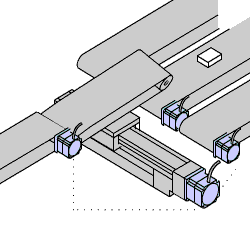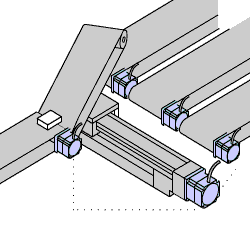 |  |
Equações
O circuito elétrico da armadura e o diagrama de corpo livre do rotor CC são mostrados na figura a seguir:
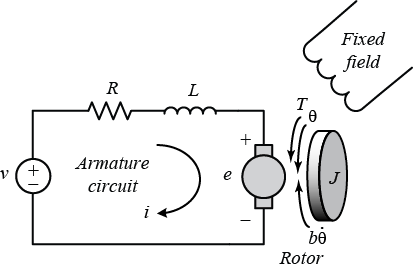
Para este exemplo, iremos supor que a entrada do sistema é a fonte de tensão () aplicada à armadura do motor, enquanto a saída é a velocidade de rotação do eixo (ou velocidade angular, ). O rotor e o eixo são considerados rígidos. Assumimos ainda um modelo de atrito viscoso, ou seja, o torque de atrito é proporcional à velocidade angular do eixo.
Os parâmetros físicos para nosso exemplo são:
| Parâmetro | Descrição | Valor (Unidades) |
|---|---|---|
| Momento de inércia d motor | 0,01 () | |
| Constante de atrito viscoso do motor | 0,1 () | |
| Constante de força eletromitia | 0,01 () | |
| Constante de torque do motor | 0,01 () | |
| Resistência elétrica | 1 () | |
| Indutância elétrica | 0,5 () |
Em geral, o torque gerado por um motor C é proporcional à corrente da armadura e à força do campo magnético. Neste exemplo, vamos assumir que o campo magnético é constante e, portanto, que o torque do motor é proporcional apenas à corrente da armadura por um fator constante conforme mostrado na equação abaixo. Isso é conhecido como motor controlado por armadura:
A força contra-eletromotriz (f.e.m.), , é proporcional à velocidade angular do eixo por um fator constante :
Em unidades SI, o torque do motor e a constante f.e.m. são iguais, ou seja, ; portanto, usaremos para representar a constante de torque do motor e a constante de f.e.m. posterior.
Este sistema será modelado somando os torques que atuam na inércia do rotor e integrando a aceleração para obter a velocidade. Além disso, as leis de Kirchoff serão aplicadas ao circuito de armadura.
Primeiro, vamos modelar as integrais da aceleração rotacional e da taxa de variação da corrente da armadura:
Modelo no Simulink
Para construir o modelo de simulação, abra o Simulink e abra uma nova janela de modelo. Em seguida, siga as etapas listadas abaixo.
- Insira um bloco Integrador da biblioteca Simulink >> Continuous, e desenhe linhas para seus terminais de entrada e saída.
- Rotule a linha de entrada "d^2/dt^2 (theta)" e a linha de saída "d/dt (theta)" conforme mostrado abaixo. Para adicionar esse rótulo, clique duas vezes no espaço vazio logo abaixo da linha.
- Insira outro bloco integrador acima do anterior e desenhe linhas para seus terminais de entrada e saída.
- Rotule a linha de entrada "d/dt(i)" e a linha de saída "i".
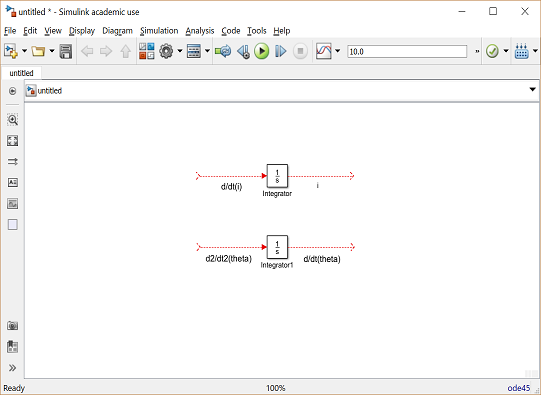
A seguir, vamos aplicar a lei de Newton e a lei de Kirchhoff ao sistema do motor para gerar as seguintes equações:
e:
A aceleração angular, , é igual a multiplicado pela soma de dois termos (um positivo, um negativo).
Da mesma forma, a derivada da corrente, , é igual a multiplicado pela soma de três termos (um positivo, dois negativos).
Continuando a modelar essas equações no Simulink, siga as etapas fornecidas abaixo:
- Insira dois blocos de ganho da biblioteca Simulink >> Math Operations, um associada a cada um dos integradores.
- Edite o bloco Gain correspondente à aceleração angular clicando duas vezes nele e alterando seu valor para
1/J(propriedades). - Mude o rótulo deste bloco de ganho para "Inércia" clicando na palavra "Gain" abaixo do bloco.
- Da mesma forma, edite o outro valor de Ganho para
1/Le seu rótulo para "Indutância". - Insira dois blocos Add da biblioteca Simulink >> Math Operations, cada um associado com uma linha a cada um dos blocos Gain.
- Edite os sinais do bloco Add correspondente à rotação para
+ -, uma vez que um termo é positivo e outro é negativo (importante não confundir sequencia dos sinais). - Edite os sinais do outro Add bloco a
- + -para representar os sinais dos termos na equação elétrica.
O resultado esperado é mostrado na próxima figura:
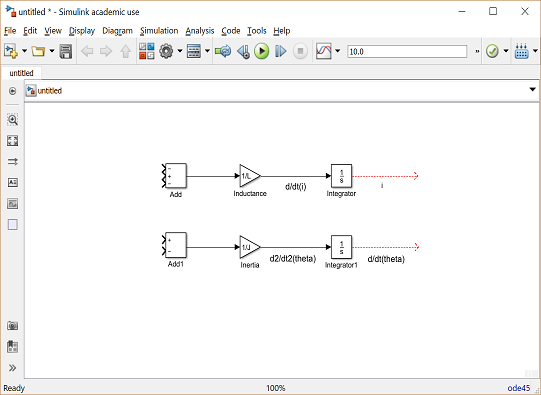
Agora, vamos adicionar os torques que são representados na equação de rotação. Primeiro, vamos adicionar o torque de amortecimento:
- Insira um bloco de Gain abaixo do bloco "Inércia". Em seguida, clique com o botão direito do mouse no bloco e selecione Rotate & Flip > Flip Block (Girar e Inverter> Inverter Bloco) no menu resultante para inverter o bloco da esquerda para a direita. Você também pode inverter um bloco selecionado mantendo pressionado
Ctrl-I. - Defina o valor de ganho para
be renomeie este bloco para "Amortecimento". - Toque em uma linha (segure
Ctrlenquanto desenha ou clique com o botão direito na linha) fora da saída do integrador rotacional e conecte-a à entrada do bloco "Amortecimento". - Desenhe uma linha da saída do bloco "Amortecimento" até a entrada negativa do bloco Add rotacional.
A seguir, adicionaremos o torque da armadura.
- Insira um bloco Gain anexado à entrada positiva do bloco Add rotacional com uma linha.
- Edite seu valor para
Ktpara representar a constante do motor e rotule-o como "Kt". - Continue desenhando a linha que sai do Integrador atual e conecte-o ao bloco "Kt".
O resultado esperado é mostrado à seguir:
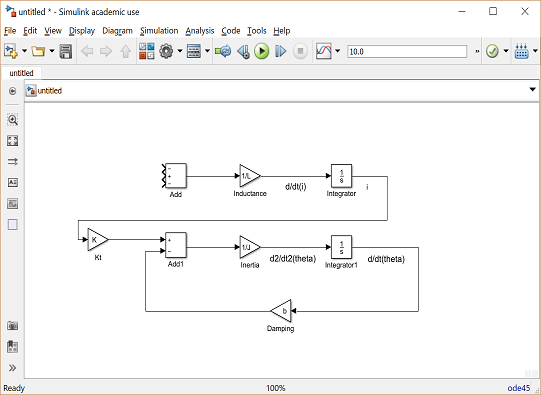
Agora, vamos adicionar os termos de tensão que são representados na equação elétrica.
Primeiro, adicionaremos a queda de tensão na resistência da armadura:
- Insira um bloco de Gain acima do bloco de "Indutância" e gire-o da esquerda para a direita (Flip).
- Defina o valor de ganho para
Re renomeie este bloco para "Resistência". - Toque em uma linha da saída do integrador atual e conecte-a à entrada do bloco "Resistência".
- Desenhe uma linha da saída do bloco "Resistência" para a entrada negativa superior do bloco Add da equação atual.
Em seguida, adicionaremos a fem traseira do motor.
- Insira um bloco Gain anexado à outra entrada negativa do bloco Add atual com uma linha.
- Edite seu valor para
Kepara representar a constante emf de retorno do motor e rotule-o como "Ke". - Toque em uma linha da saída do integrador rotacional e conecte-a ao bloco "Ke".
- Adicione blocos In1 e Out1 da biblioteca Simulink >> Ports & Subsystems e, respectivamente, rotule-os de "Voltagem" e "Velocidade".
O design final deve ser semelhante ao exemplo mostrado na figura abaixo:
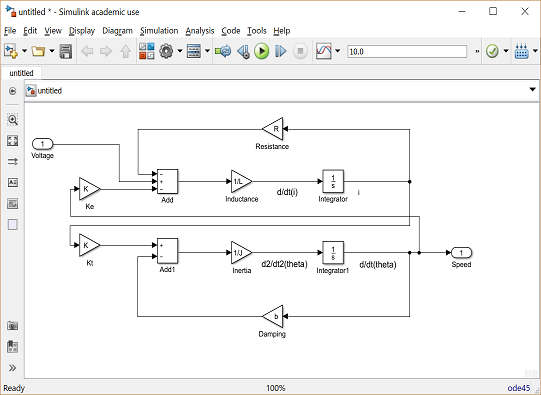
E para salvar todos esses componentes como um único bloco de subsistema, primeiro selecione todos os blocos e, em seguida, selecione Criar Subsistema a partir da Seleção após clicar com o botão direito do mouse na parte selecionada. Nomeie o subsistema "Motor DC" e salve o modelo. Seu modelo deve ficar com a seguinte aparência.
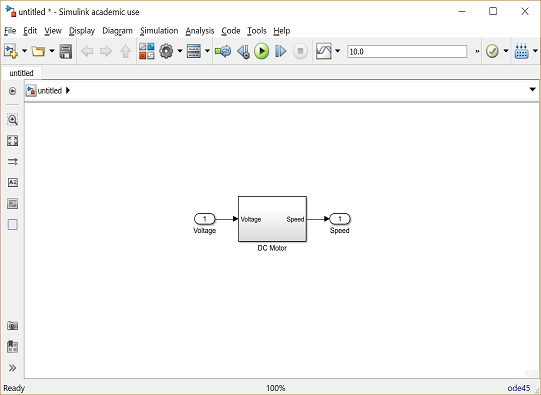
Alguns exemplos de controle de Velocidde deste motor aparecem originalmente aqui: DC Motor Speed: Simulink Controller Design (em inglês).
No nosso caso, resolvi acrescentar um segundo nó de saída: corrente do motor, para propiciar o monitoramento de eventuais correntes elevadas exigidas pelo motor. Foi acrescentado um bloco Out2 associado com “Corrente”. O diagrama de blcoos final do modelo do motor antes da criação so subsistema aparece na próxima figura:
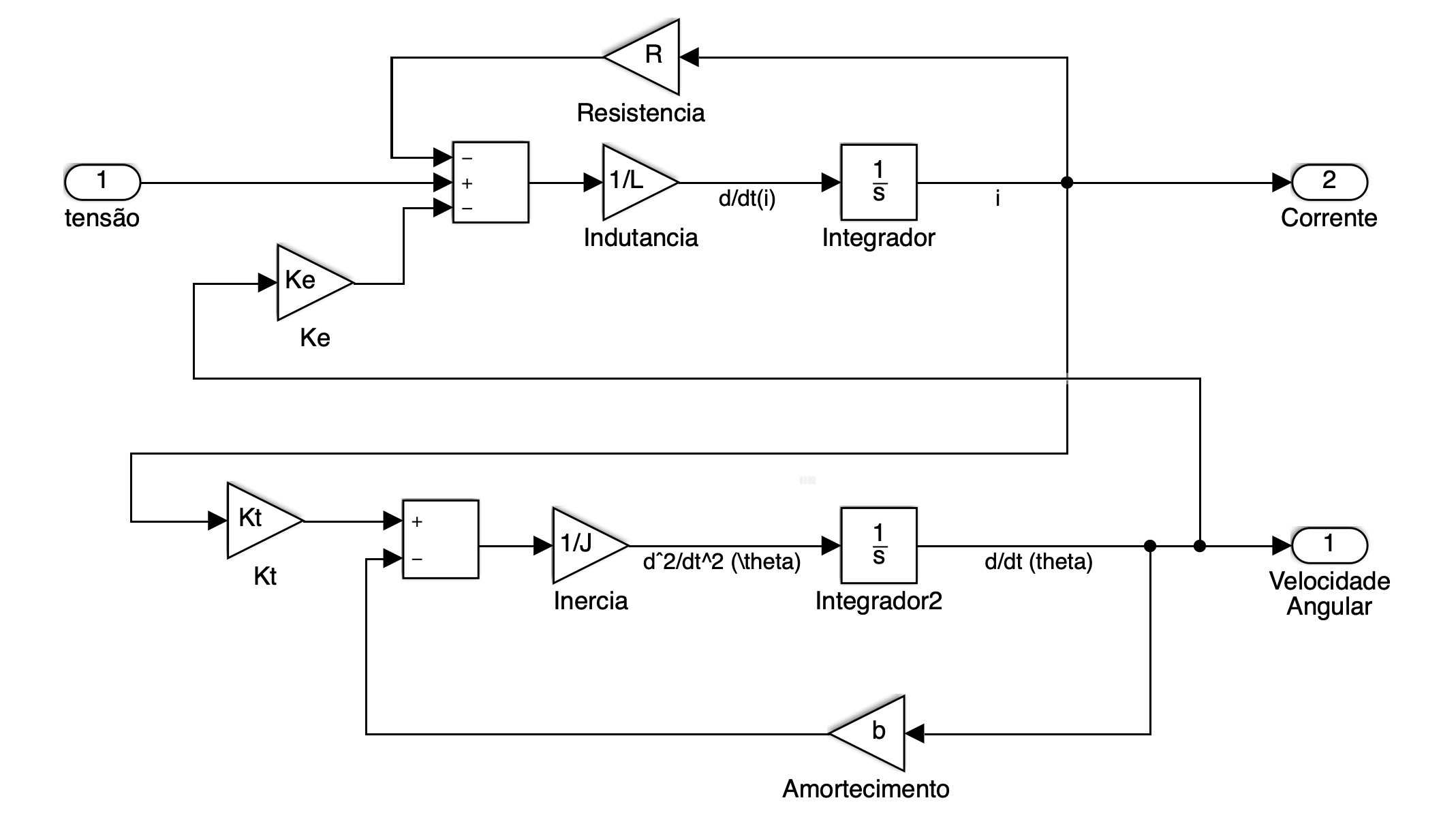
Você também pode baixar o arquivo pronto deste sistema: motor_cc_velocidade.slx (ou motor_cc_velocidade.mdl ).
Obs.: arquivos SLX refletem a versão usada do Matlab/Simulink. Arquivos MDL são mais antigos e independem da versão do Matlab (não suportam código UTF/caracteres com acentuação entre outros detalhes). Se tiver problemas em abrir o arquivo SLX, tente abrir o arquivo MDL.
Note que: para este modelo ser usado, é necessário atribuir valores para as variáveis R, L, Ke, Kt, J e b (que aparecem dentro das propriedades de alguns blocos presentes na figura/modelo mostrado na figura anterior). Para facilitar o carregamento destas variáveis no Workspace do Matlab, deve ser executado o script motor.m. ⚠️
Que transformado num sub-sistema resulta no arquivo motor_cc_velocidade.slx (ou motor_cc_velocidade.mdl ) :
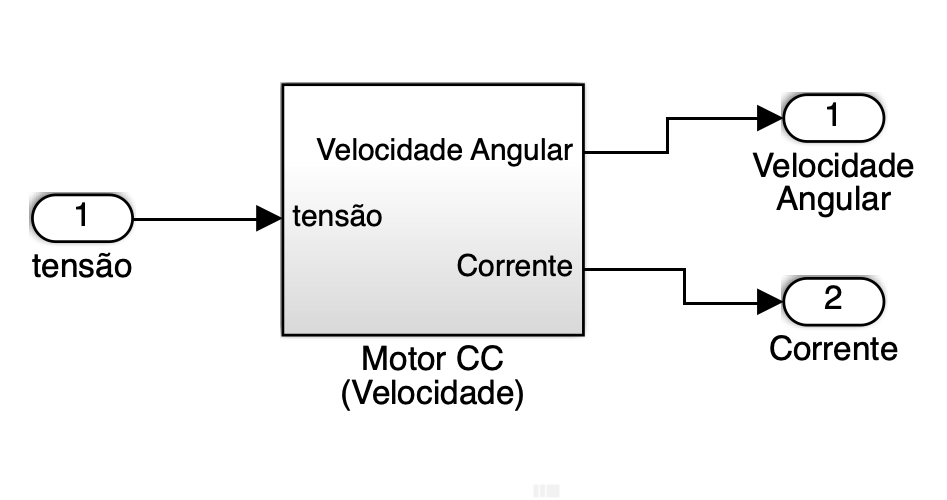
Teste do Modelo
Teste de controle em Malha aberta (arquivo: motor_cc_velocidade_teste_MA.slx ou motor_cc_velocidade_teste_MA.mdl ):
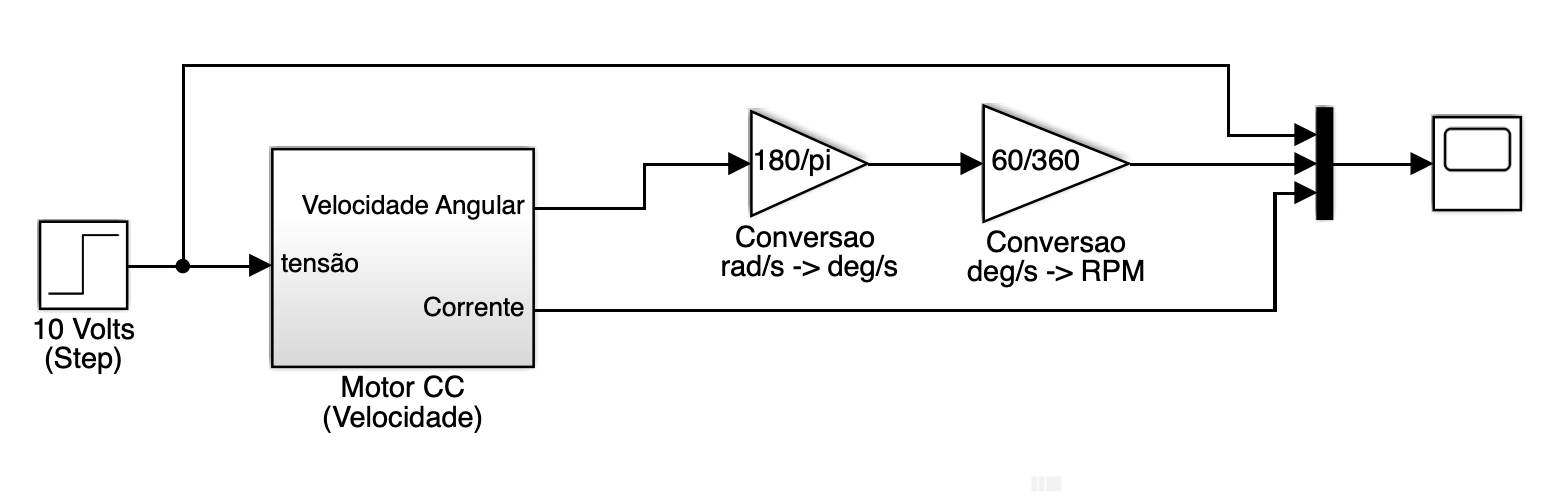
Obs.: novamente, antes de simular o bloco acima, não esquecer de executar o script motor.m na janela de comandos do Matlab.
Note que neste caso, estamos alimentando o motor com 10 Volts (referência/entrada degrau) e monitorando a velocidade de saída, não em mas em RPM (por isto os blocos Gain de conversão para converter do sistema SI para RPM):
Resultado esperado:
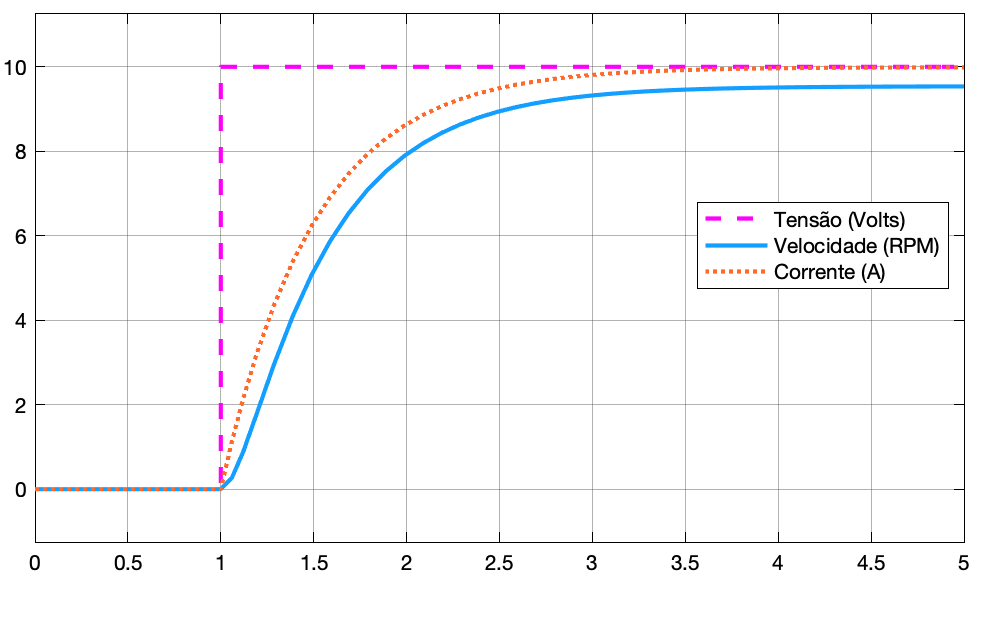
Note que aplicando 10 Volts na entrada (no motor), o mesmo quase alcança 10 RPMs de velocidade (de saída).
Exemplos de Ações de Controle em Velocidade de Motor CC
1. Controlador Proporcional
Fechando uma malha de controle Proporcional de velocidade para este motor, para tentar manter velocidade em 10 RPM (arquivo: motor_cc_velocidade_cont_Prop.slx ou motor_cc_velocidade_cont_Prop.mdl ):
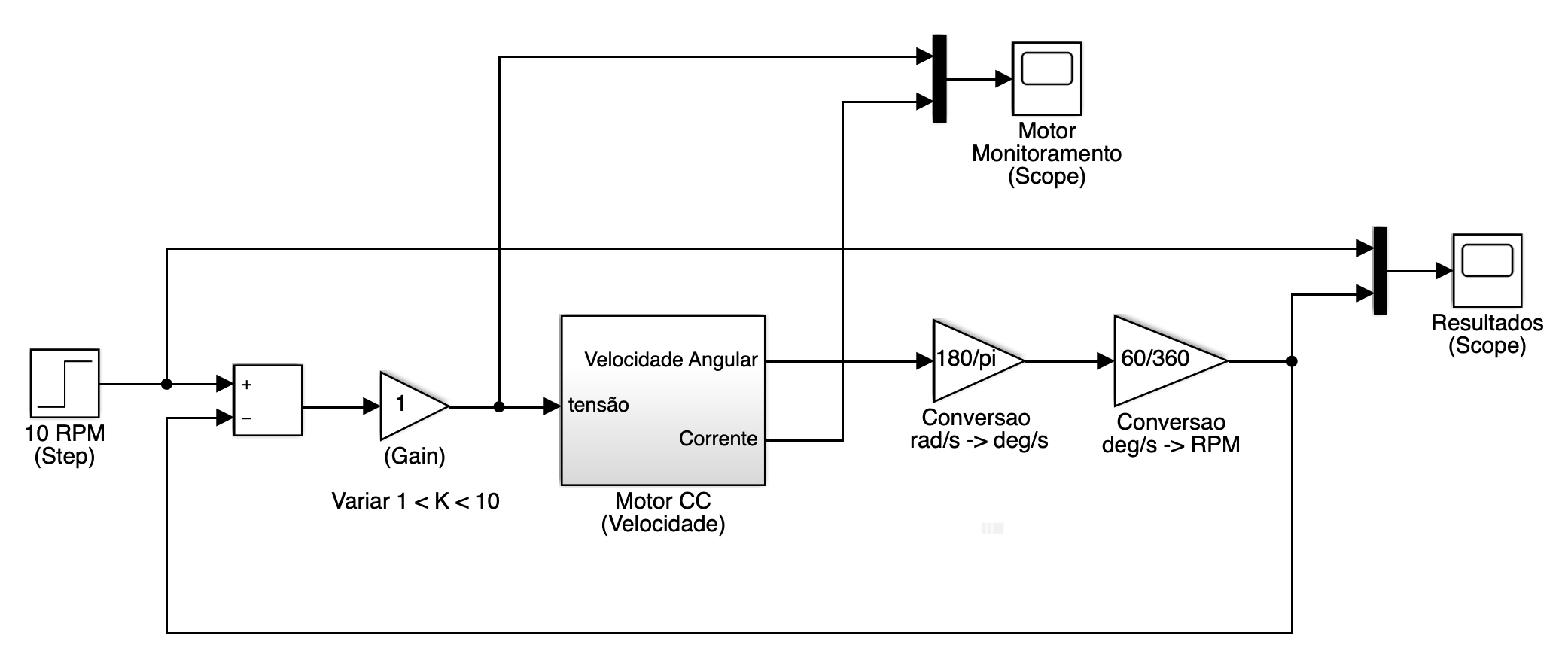
Obs.: antes de simular o bloco acima, não esquecer de executar o script motor.m na janela de comandos do Matlab.
A simulação do bloco anterior resulta em:
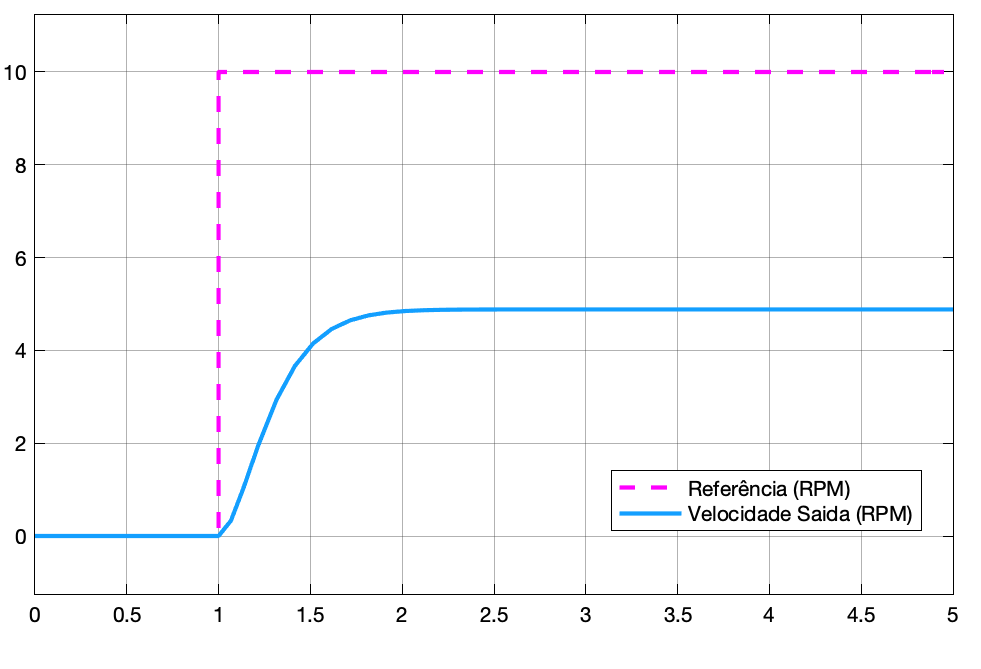 | 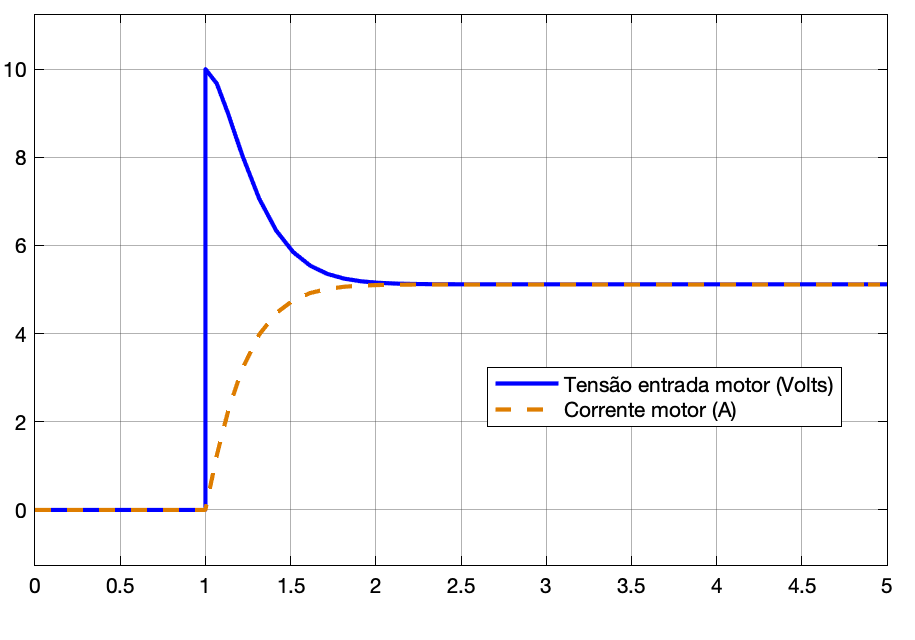 |
|---|---|
| Saída do Processo | Monitoramento do Motor |
Obs.: Varie o valor do ganho Proporcional (bloco "gain") e observe o que acontece. O erro deve baixar para valores elevados de ganho.
2. Controle PI
Fechando uma malha de controle PI (Proporcional-Integral) de velocidade para este motor, para tentar manter velocidade em 10 RPM (Arquivo: motor_cc_velocidade_cont_PI.slx ou motor_cc_velocidade_cont_PI.mdl ):
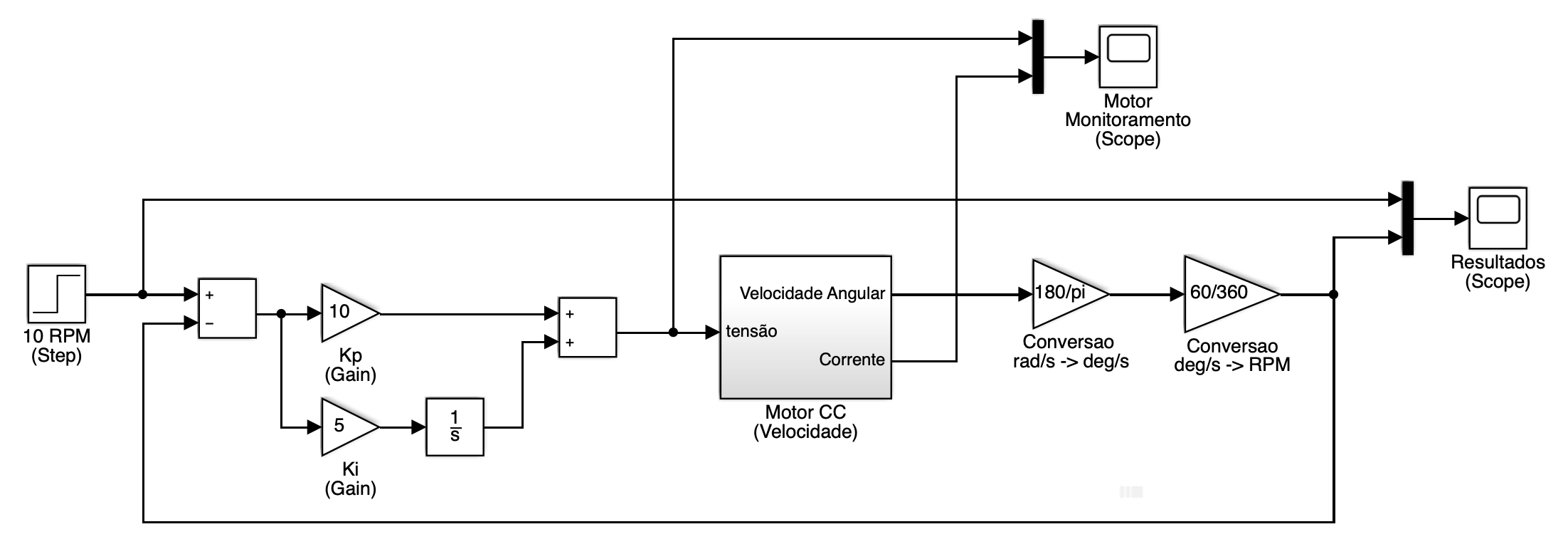
Que resulta em:
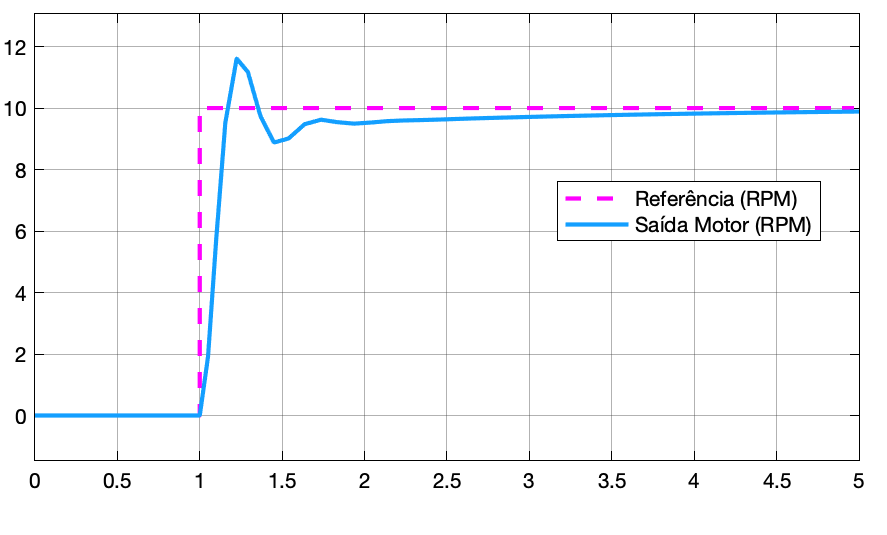 | 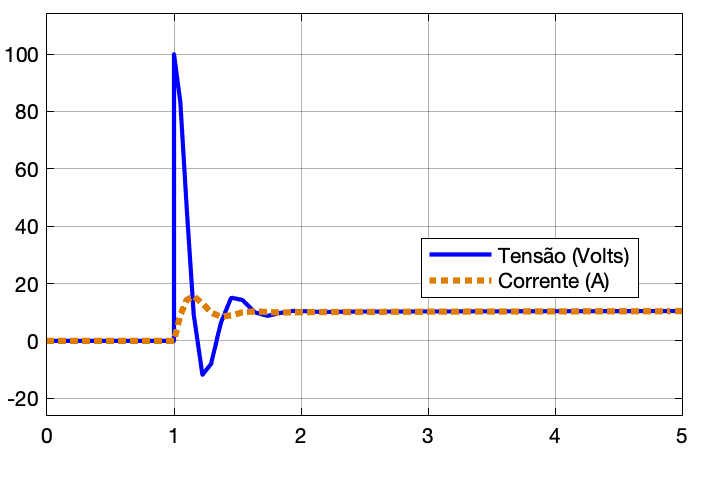 |
|---|---|
| Saída do Processo | Monitoramento do Motor |
Obs.: Varie (um de cada vez), os valores dos ganhos da ação Proporcional () e da ação Integral (). Note que mesmo que o ganho da ação integral seja baixo, o saída do sistema ainda converge para o valor desejado de saída () culminando em erro nulo em regime permanente ().
3. Controle PD
Fechando uma malha de controle PD (Proporcional-Derivaito) de velocidade para este motor, para tentar manter velocidade em 10 RPM (Arquivo: motor_cc_velocidade_cont_PD.slx ou motor_cc_velocidade_cont_PD.mdl ):
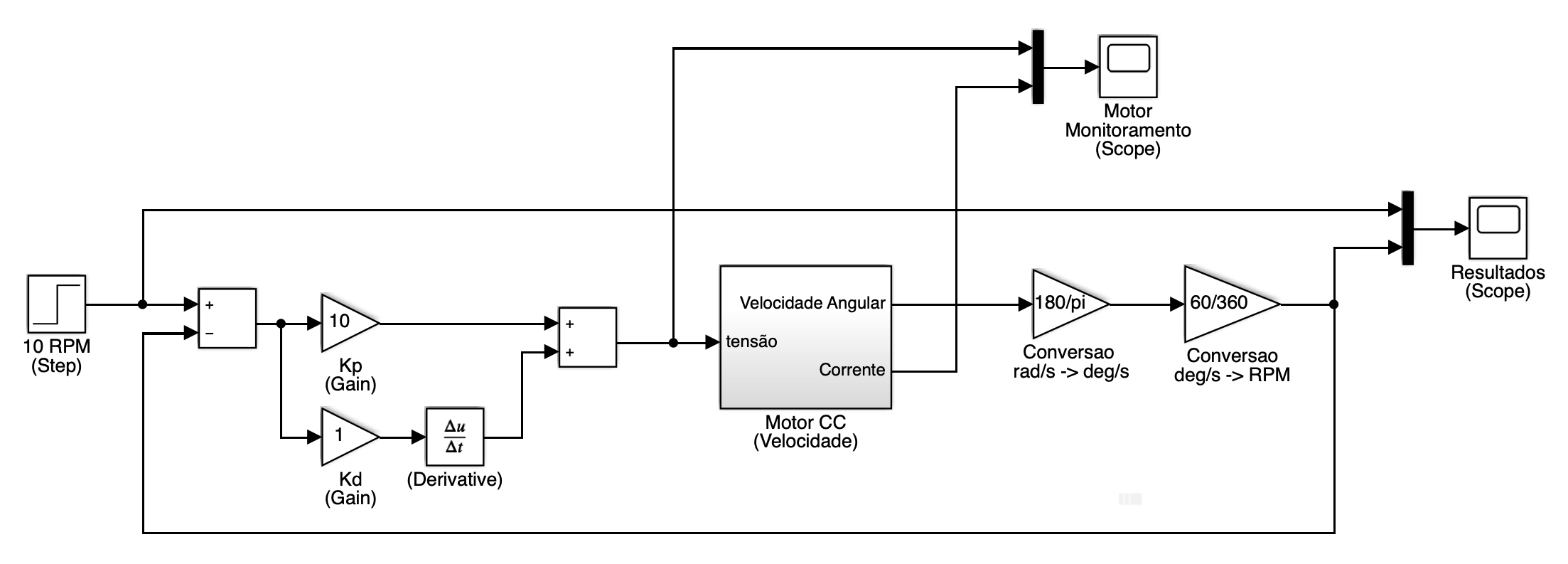
Resultados:
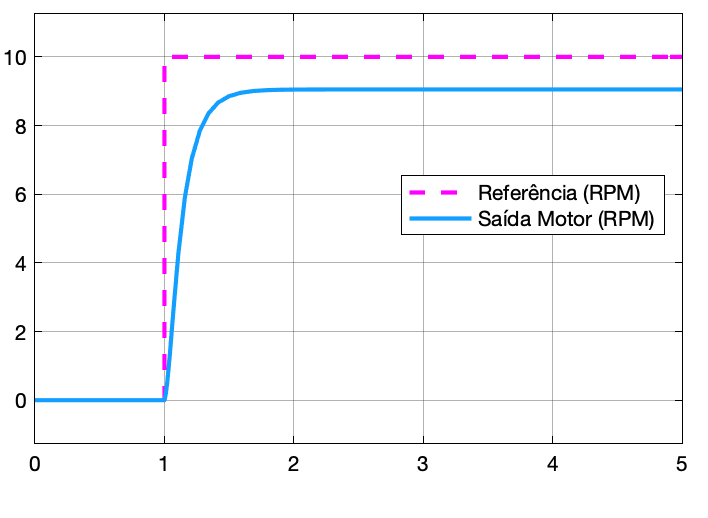 | 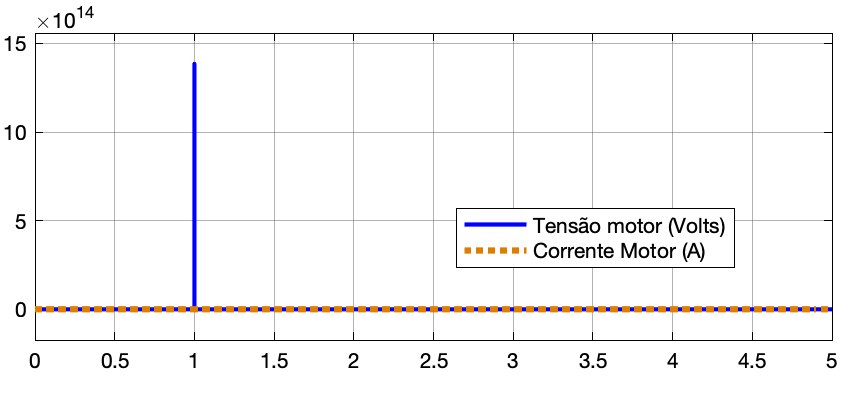 |
|---|---|
| Saída do Processo | Monitoramento do Motor |
Obs.: Varie (um de cada vez), os valores dos ganhos Proporcional () e da ação Derivativa (). Note que não importa os valores adotados sempre existirá um erro. Note ainda que valores elevados para estes ganhos vão produzir mais oscilações (overshoots) aumentando consideravelmente o tempo de assentamento (tempo de resposta) do sistema. Perceba ainda que um controlador PD "força" muito mais o sistema, gerando elevadas amplitudes para sinal de controle (sinal de atuação sobre o processo); na prática, muitas vezes saturando o driver de potência usado para enviar potência para o sistema (motor no caso). Mas perceba que o controlador PD, se bem sintonizado, faz o sistema reagir de forma muito mais rápida se comparado à um controlador PI ou P.
4. Controle PID
Fechando uma malha de controle PID (Proporcional-Integrativo-Derivaito) de velocidade para este motor, para tentar manter velocidade em 10 RPM (Arquivo: motor_cc_velocidade_cont_PID.slx ou motor_cc_velocidade_cont_PID.mdl ):
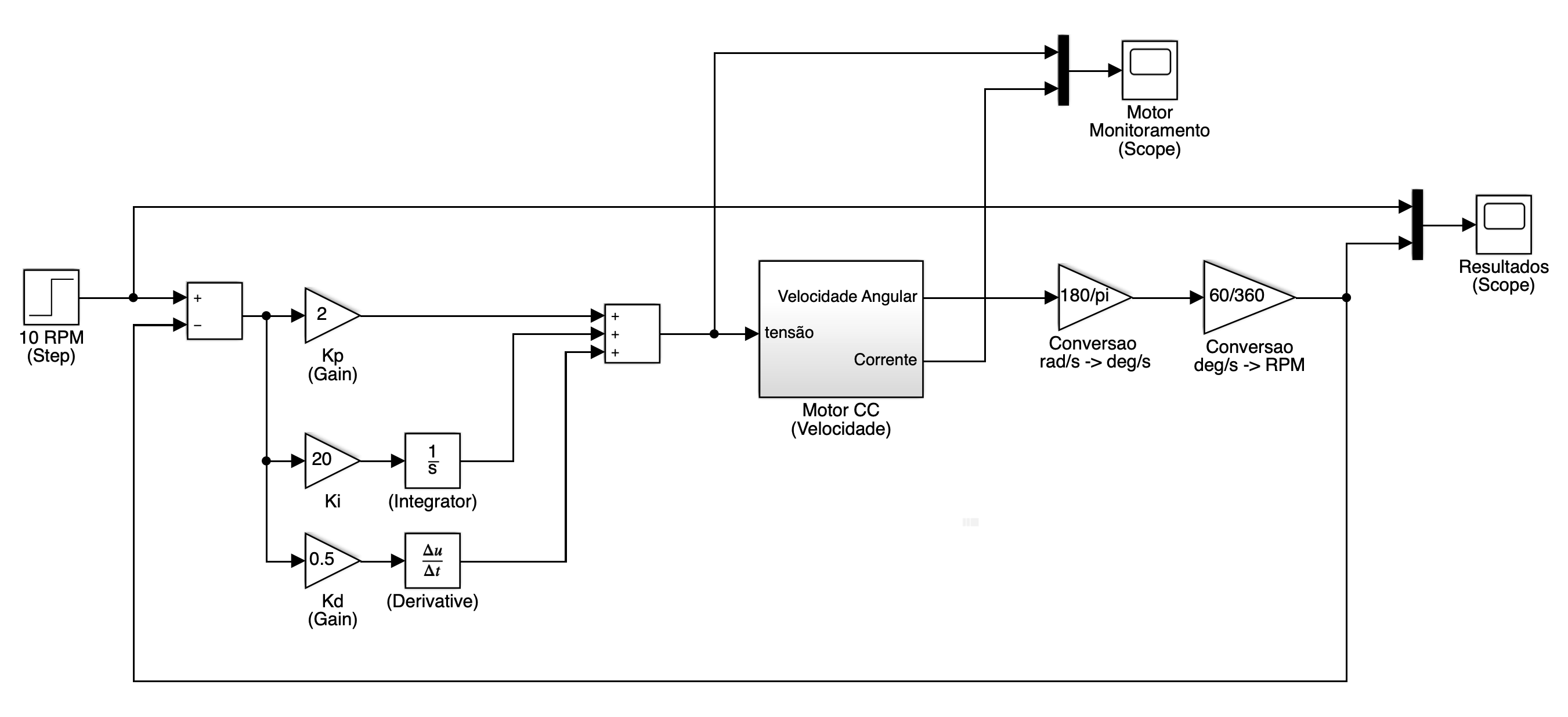
Resultados:
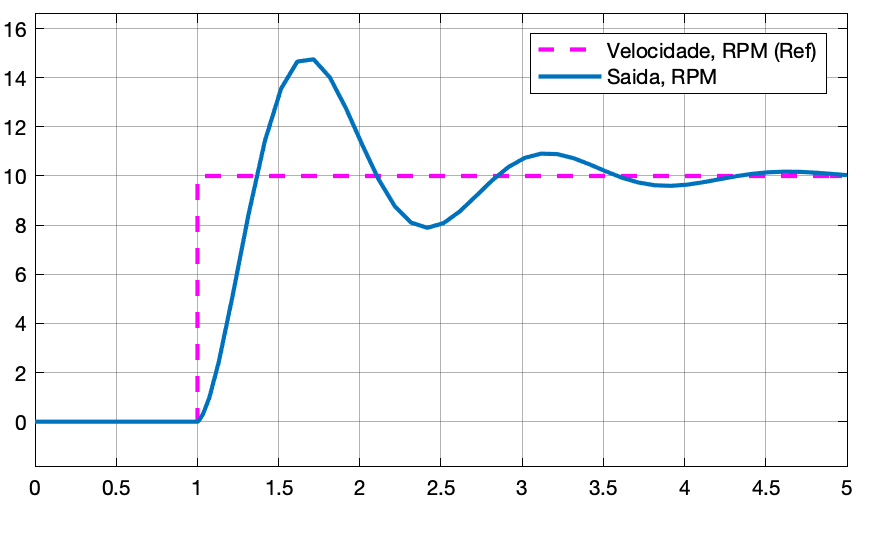
Obs.: variar (um de cada vez) os 3 ganhos (um para cada ação de controle, , e ). Deve ser observado que a ação Derivativa deve acelerar a resposta do sistema (deste que não tenha sido usado um valor exagerado). A ação Integral garante erro nulo em regime permanente e a Ação Proporcional permite acelerar a resposta do sistema (mas não de forma tão rápida quanto a ação Derivativa).
Conclusão final
A idéia, com os exemplos mostrados anteriormente, é que você varie os ganhos dos controladores e observe o que acontece e perceba que pode ser bastante complicado ajustar empiricamente os ganhos de controladores com 2 parâmetros de ajuste ou mais.
Dependendo da planta/sistema à ser controlador, mesmo um controlador Proporcional pode levar um sistema à instabilidade se forem usados valores muito elevados.
Falta ver 3. Teoria do Erro para entender como se pode controlar/restringir erros num sistema de malha fechada e falta ver 4. Teoria sobre Estabilidade para entender e prever valores máximos de ganhos que podem ser adotados num sistema em malha-fechada.
Um “pacote” (bag) de todos os arquivos necessários para as simulações está disponível aqui.
Fernando Passold, em 31/08/2020; última atualização em 21.08.2025.