Melhorias em controlador Proporcional !?

Seja a planta:

Um controlador Proporcional para a mesma, limitando $\%OS \le 20\%$, ficaria:

>> G=tf ( 3, 100*poly([-3/5 -2/5 -1/10]) );

Realizando o RL para este sistema, encontraremos um ganho próximo de 2.

Fechando a malha, teremos uma resposta como:

>> ftmf_K1=feedback(2*G, 1);
>> step(ftmf_K1)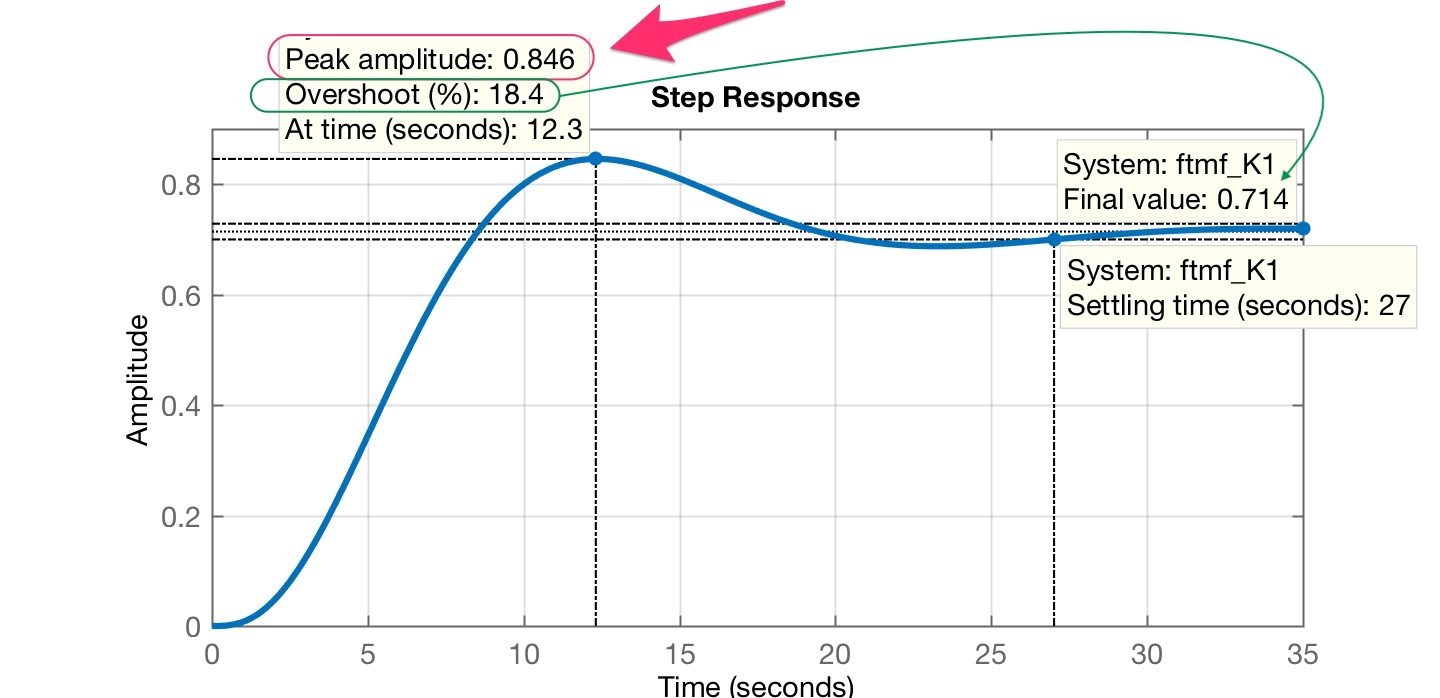

Note que o $\%OS$ mostrado pelo Matlab na figura se refere ao valor em regime permanente atingido pela planta ($y(\infty)$), mas não corresponde ao overshoot máximo (ou sobresinal máximo) admitido para a referência que deveria fazer a planta alcançar o valor final unitário e não $y=0,714$ como neste caso.

Isto significa que podemos aumentar o ganho neste sistema (desde que ele não fique estável) e tentando obedecer ao sobressinal máximo de 20% em relação ao valor final que a referência deveria atingir ($y(t \to \infty)=1,0$), o que significa neste caso, que o controlador à ser projetado aqui, poderia forçar a planta à atingir picos de no máximo $M\acute{a}x \{ y(t) \}= 1,2$.

Supondo que com $K_2=4$ possamos fazer a planta chegar próximo deste patamar máximo, podemos fazer:

>> ftmf_K2=feedback(4*G, 1);
>> step(ftmf_K1, ftmf_K2)
>> legend('Kp=2' , 'Kp=4')

O que rederia a figura:

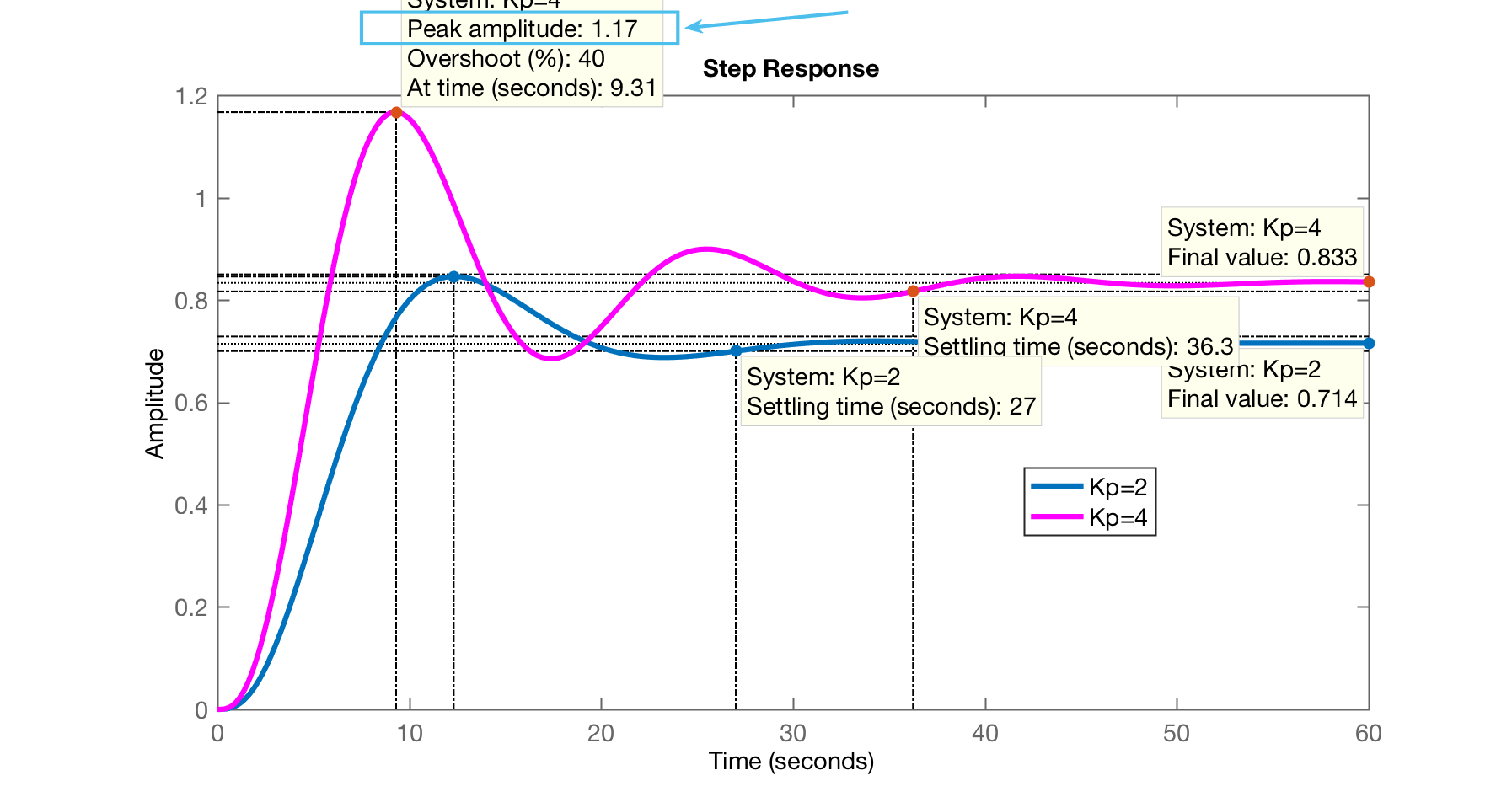
Notamos que com $K_p=4$, a amplitude de saída da planta aumenta, o sobressinal também: $M\acute{a}x\{ y(t) \}\big|_{K_p=4}=1,17$ , mas ficando ainda abaixo dos 20% máximo permititos.

Aumentar o ganho fez o erro baixar: $y(\infty)\big|_{K_p=4}=0,833 \Rightarrow e(\infty)\big|_{K_p=4}=16.7\%$; contra antes: $y(\infty)\big|_{K_p=2}=0,714 \Rightarrow e(\infty)\big|_{K_p=2}=28.6\%$,

apesar de aumenar o tempo de assentamento do sistema, de $t_s=27$ para $t_s=36,4$.

A questão agora para decidir por qual valor de ganho adotar passa por: -- o que é prioritário? Menor erro ou menor tempo de assentamento?

Mesmo que seja adotado o maior ganho, ainda percebemos que este sistema em MF (malha-fechada) responde um pouco mais rápido que o sistema em MA (malha-aberta): $t_{s}\big|_{MA}=43,8$ segundos:

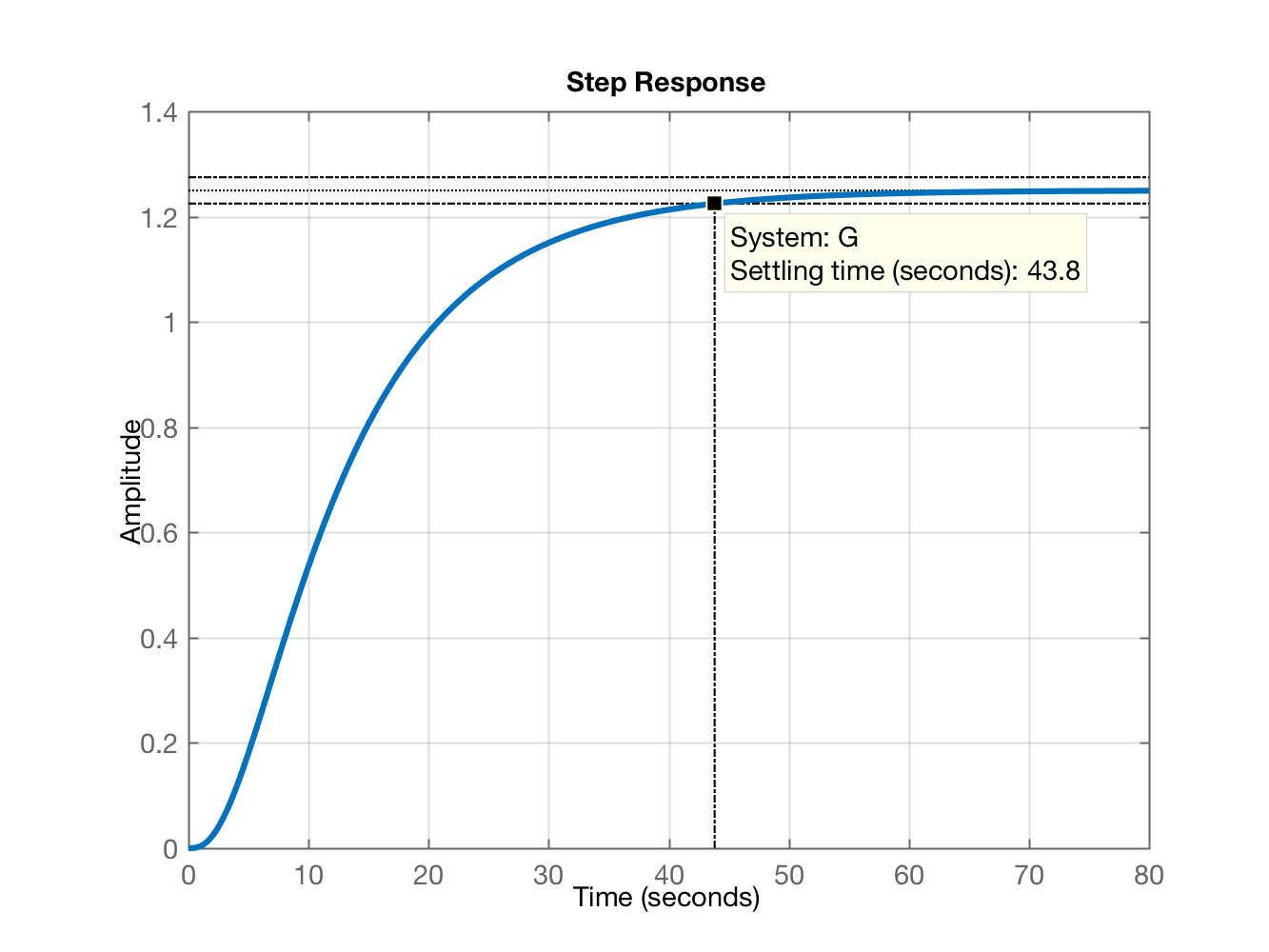
Amplitudes das Ações de Controle

Adotar um ganho mais elevado vai implicar em expor à planta à maiores valores de atuação.

Existe uma forma prática de forçar o Matlab a mostrar as amplitudes geradas por certo controlador, SEM apelar para o Simulink. Para tanto necessitamos realizar uma ligeria manipulação algébrica:

De um sistema com realimentação unitária negativa sabemos que:

(1) $U(s)=C(s) \cdot E(s)$

(2) $E(s)=R(s)-Y(s)$

(3) $Y(s)=U(s) \cdot G(s)$

Substituindo (2) em (1) teremos:

(4) $U(s)=C(s) \left[ R(s) - Y(s) \right]$

$U(s)=C(s)R(s)-C(s)Y(s)$

E podemos ainda substituir (3) em (4), o que resulta em:

$U(s)=C(s)R(s)-C(s)G(s)U(s)$

trabalhando a eq. anterior, podemos escrever:

$U(s)\left[ 1 +C(s)G(s) \right]=C(s)R(s)$

(5) $U(s)=\dfrac{C(s)R(s)}{1+C(s)G(s)}$

A eq. (5) é a que vai nos permitir usar a linha de comandos do Matlab para plotar $u(t)$.

Se você já reparou antes, quando realiza o comando:

​x
>> step(ftmf_exemplo)     % Resposta ao degrau no domínio tempo

Você está pedido que o Matlab faça o seguinte:

1. $Y(s)=ftmf\_exemplo(s)\cdot R(s)$, onde $R(s)$ corresponde à transformada de Laplace da função Degrau;
2. $y(t) = \mathcal{L}^{-1} \{ Y(s) \}$, implica algebricamente a realizar expansão em frações parciais para resolver esta transformada. Pois bem, o Matlab não resolve este problema algebricamente e sim numericamente.
3. Por fim, o Matlab cria internamente um vetor $t$ (tempo) varianando de $0 \le t \le t_{fim}$, onde $t_{fim}$ é um valor estipulado pelo algoritmo step do Matlab de tal forma que corresponda ao $t_s$.
4. O Matlab finalmente realiza algo como: plot (t,y).

Então, no nosso caso agora, necessitamos que o Matlab plote $t \times u(t)$ baseado na eq. (5) que deduzimos anteriormente.

Note que podemos adaptar a função step do Matlab para que a mesma plote $u(t)$ ao invés de $y(t)$, bastando neste caso, fornecer adequandamente uma nova função transferência. Note que toda função step multiplica a transfer function passada como argumento de entrada pela transformada de Laplace da entrada degrau e segue com o processamento citado anteriormente até finalizar o no gráfico.

Baseado na eq. (5), basta repassar então a seguinte transfer function à função step:

Se (5): $U(s)=\left[ \dfrac{C(s)}{1+C(s)G(s)} \right] \cdot R(s)$

onde: $\left[ \dfrac{C(s)}{1+C(s)G(s)} \right]=\text{“aux”}$

Então realizar: >> step(aux) é o equivalente à plotar $u(t)$.

Aplicando esta constatação ao nosso caso:

x
>> aux_K1=2*1/(1+2*G);
>> zpk(aux_K1)
 
      2 (s+0.6) (s+0.4) (s+0.1)
  ----------------------------------
  (s+0.8078) (s^2 + 0.2922s + 0.104)
 
Continuous-time zero/pole/gain model.
​
>> aux_K2=4/(1+4*G);
>> zpk(aux_K2)
 
   4 (s+0.6) (s+0.4) (s+0.1)
  ---------------------------
  (s+0.9) (s^2 + 0.2s + 0.16)
 
Continuous-time zero/pole/gain model.
​
>> figure; step(aux_K1, aux_K2);
>> legend('Kp=2' , 'Kp=4')
>> title(string('Ações de Controle'))

Note que o resultado das expressões “aux_K1” e “aux_K2” não nos importam muito, foram mostradas anteriormente mais como curiosidade. O que importa é notar o resutlado da função step aplicada desta forma:

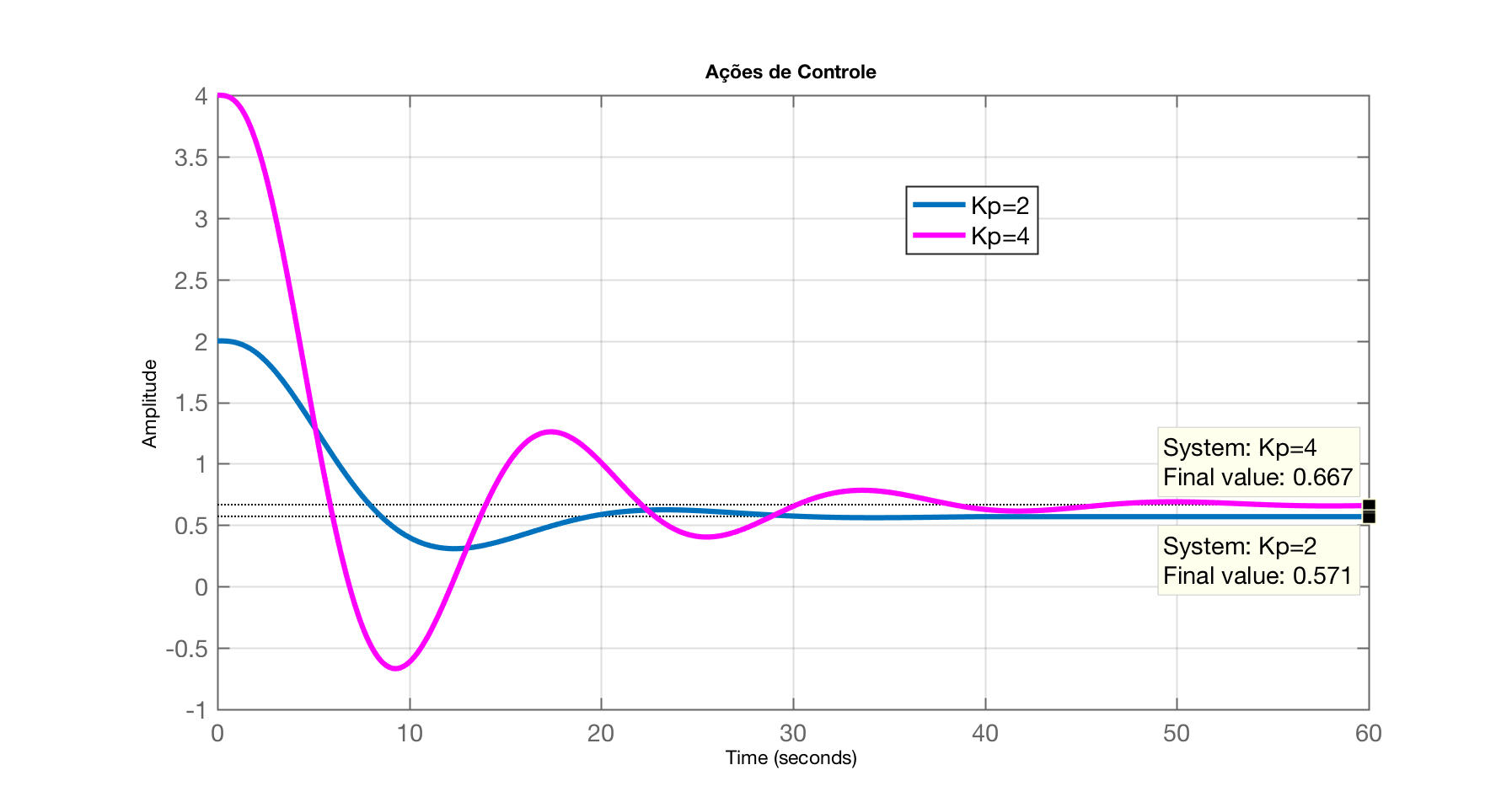
Fim.

Fernando Passold, em 04.06.2021