
Sintonia de PIDs usando Ziegler Nichols
Seja um controlador PID no formato paralelo como o mostrado no diagrama em blocos à seguir:
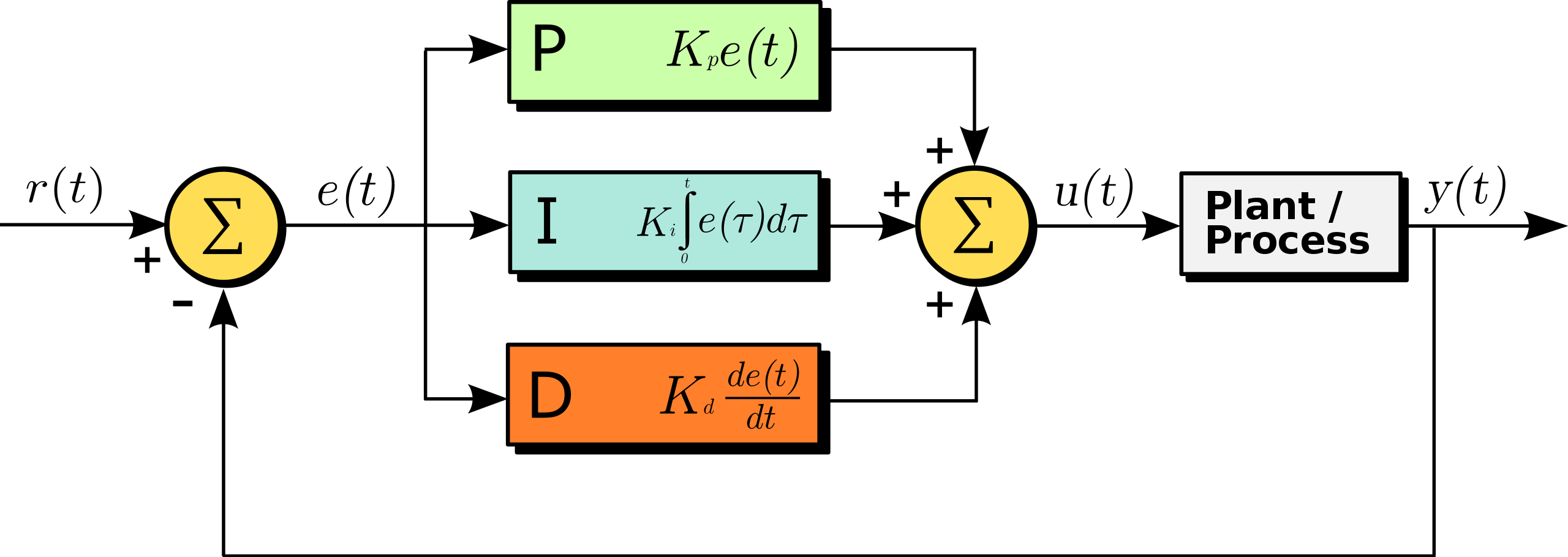
O método de ajuste de Ziegler-Nichols é um método heurístico de ajuste de um controlador PID. Foi desenvolvido por John G. Ziegler e Nathaniel B. Nichols em 1942 1.
É realizado configurando os ganhos (integral) e (derivado) para zero. O ganho "P" (proporcional), ou é então aumentado (de zero) até atingir o ganho final , que é o maior ganho no qual a saída do circuito de controle tem oscilações estáveis e consistentes (uma senóide de amplitude constante, resultado de pólos complexos sobre o eixo no plano-s). Ganhos maiores que o ganho final resultam em oscilação divergente (senoíde de amplitude constante). Interessa tomar conhecimento neste método, tanto o valor de quanto o valor do período de oscilação da senóide, .
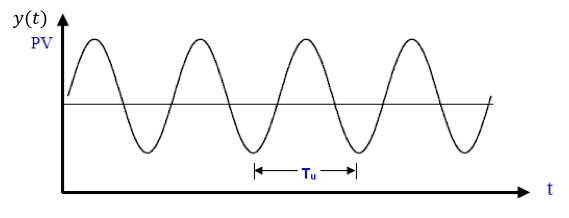
Os valores de e são usados para definir os valores iniciais para os ganhos do PID: , e , dependendo do tipo de controlador usado e comportamento desejado:
| Controlador | |||||
|---|---|---|---|---|---|
| P | - | - | - | - | |
| PI | - | - | |||
| PD | - | - | |||
| PID | |||||
| Algum sobressinal | |||||
| Sem sobressinal |
onde:
;
;
Os 3 parâmetros obedecem à equação (no formato ISA) do PID:
ou (equação no formato paralelo):
que no plano-s origina:
ou:
Como alternativa à tabela anterior, outro conjunto de valores de ajuste foi determinado por Tyreus e Luyblen para PI e PID, geralmente chamados de regras de ajuste do TLC. Esses valores tendem a reduzir os efeitos oscilatórios e melhorar a robustez.
| Controlador | |||
|---|---|---|---|
| PI | - | ||
| PID |
Método de auto-ajuste baseado no método do Relé
Existe outra maneira de sintonizar o PID usando a estrutura básica de um controlador ON/OFF, chamado de "método do relé”.
Publicado em 1984 por Karl Johan Åström e Tore Hägglund2, o método de relé opera temporariamente o processo usando o controle bang-bang (ou on/off) e mede as oscilações resultantes. A saída é alternada (como se por um relé, daí o nome) entre dois valores da variável de controle. Os valores devem ser escolhidos para que o processo cruze o ponto de ajuste, mas não necessita ser 0% e 100%; escolhendo valores adequados, podem ser evitadas oscilações perigosas num sistema real.
O procedimento neste caso é o seguinte:
- Permita o sistema se estabilizar;
- Modifique a referência (ou setpoint) para o valor desejado;
- Implemente um controlador on-off onde:
Para malha de realimentação negativa, faça: - Deixe o processo se estabilizar assumindo uma oscilação periódica sustentada (período de oscilação constante).
Note que o processo deve passar a oscilar da forma mostrada na próxima figura:
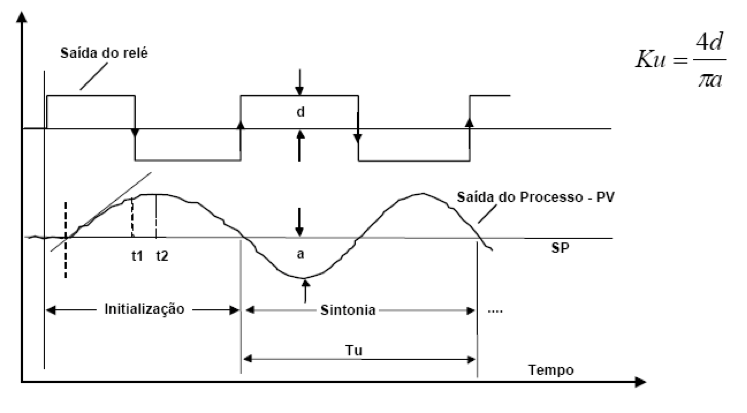
Neste caso, o valor de pode ser inferido à partir da seguinte equação:
onde: corresponde as amplitudes extras de controle acrescentadas à planta;
e corresponde ao valor de pico das oscilações presentes na resposta do sistema.
Efeitos dos parâmetros de um PID
De maneira geral o ajuste fino de um controlador PID leva em consideração os seguintes efeitos causandos quando se modificam seus parâmetros:
| Parâmetro | Estabilidade | ||||
|---|---|---|---|---|---|
| Pequena Mudança | Diminui | ||||
| Elimina | Diminui | ||||
| Pequena Alteração | Sem Efeito | Melhora se é pequeno |
A próxima figura passa uma idéia dos efeitos obtidos quando se altera os parâmetros de um PID:
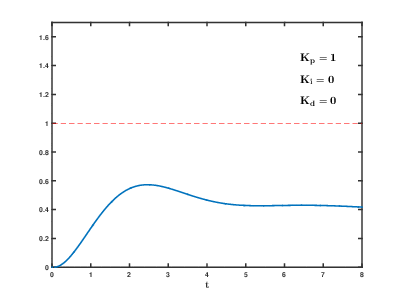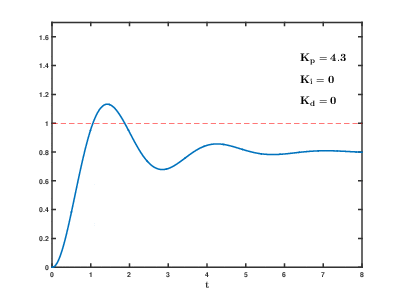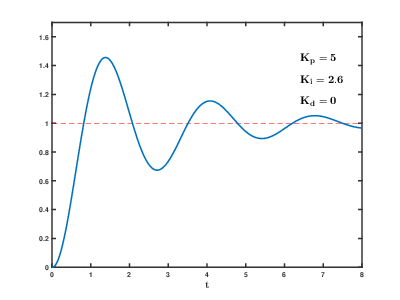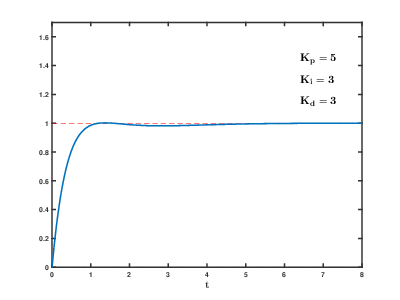
Exemplo de sintonia usando ZN
Seja o seguinte sistema:
Podemos usar o Matlab para descobrir de forma mais rápida qual seria o , ganho máximo que poderia ser aplicado neste processo (quando uma malha é fechada usando um simples controlador proporcional).
>> G=tf(1,poly([-1 -2 -10]));>> zpk(G)ans = 1 ------------------ (s+10) (s+2) (s+1) Continuous-time zero/pole/gain model.>> % caçando o ganho máximo usando RL>> rlocus(G)>> axis([-12 1 -8 8])Usando o "Data Cursor" posicionamos o mesmo sobre o traçado do RL quando o mesmo cruza o exifo , como mostrado na figura abaixo:
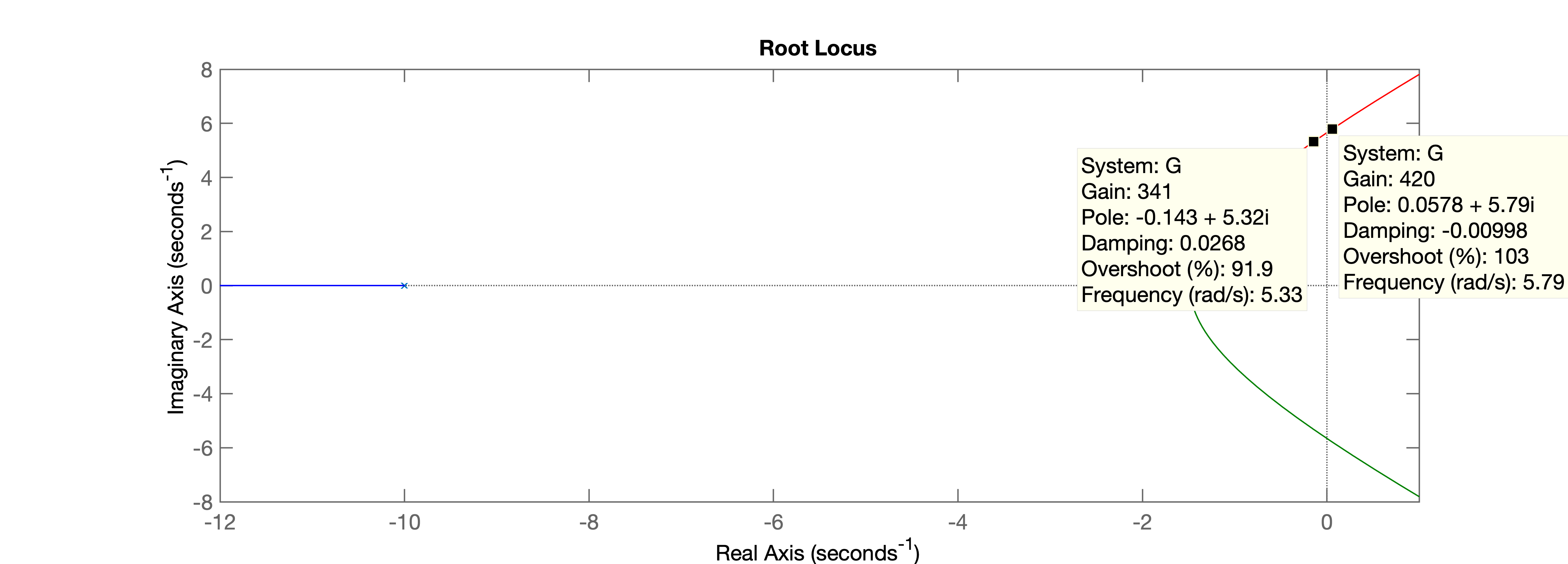
Observamos que o Matlab varia o valor do Ganho para gerar o traçado do RL e usa um passo desconhecido. Notamos pela figura que o ganho máximo neste caso, está entre .
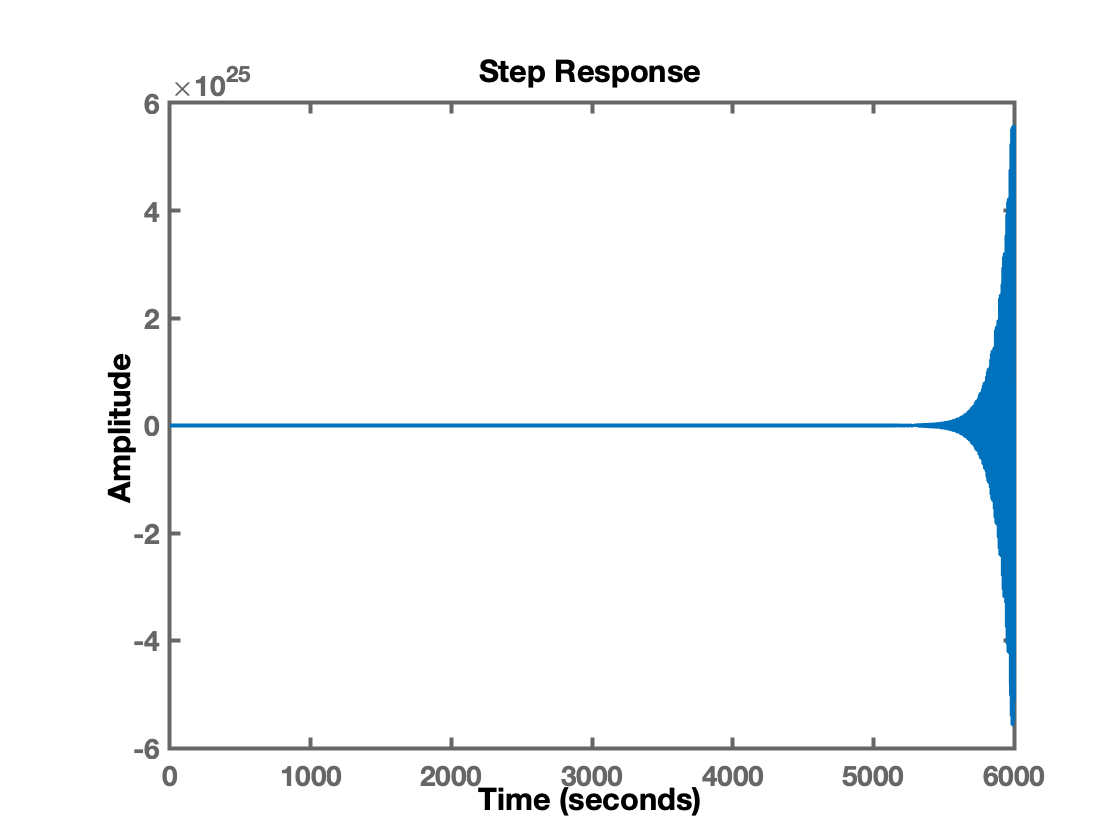
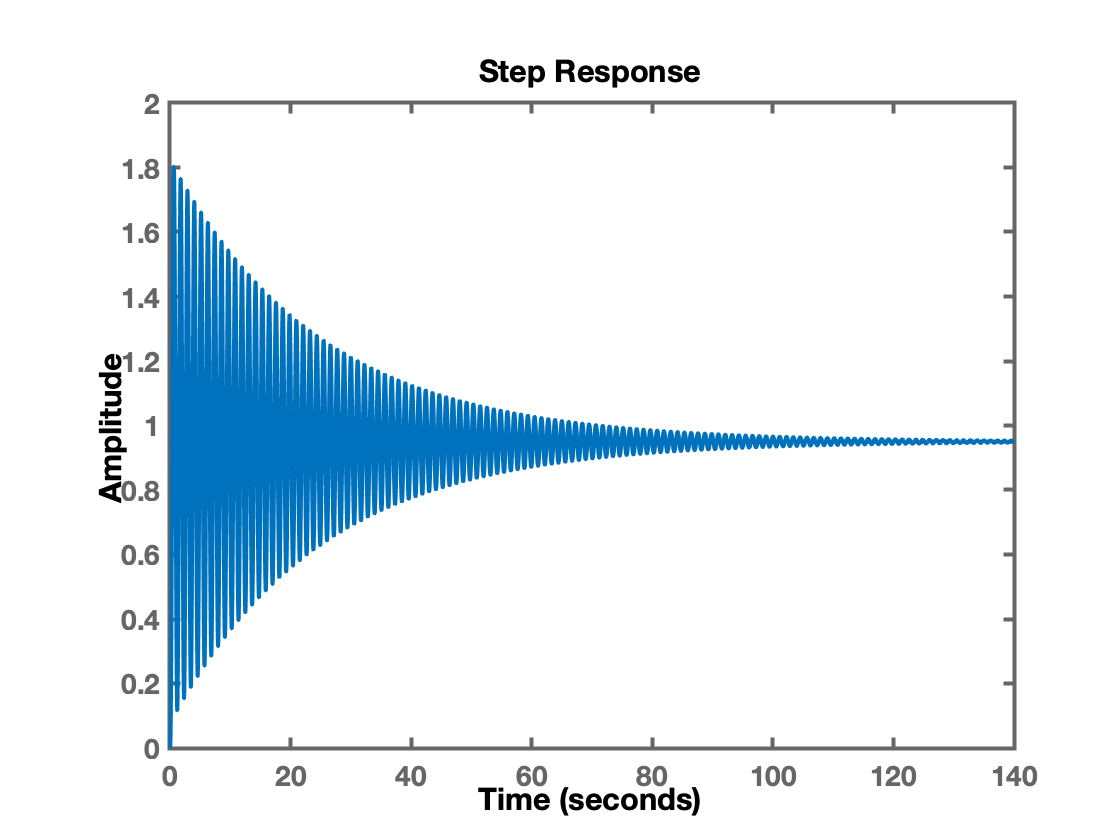
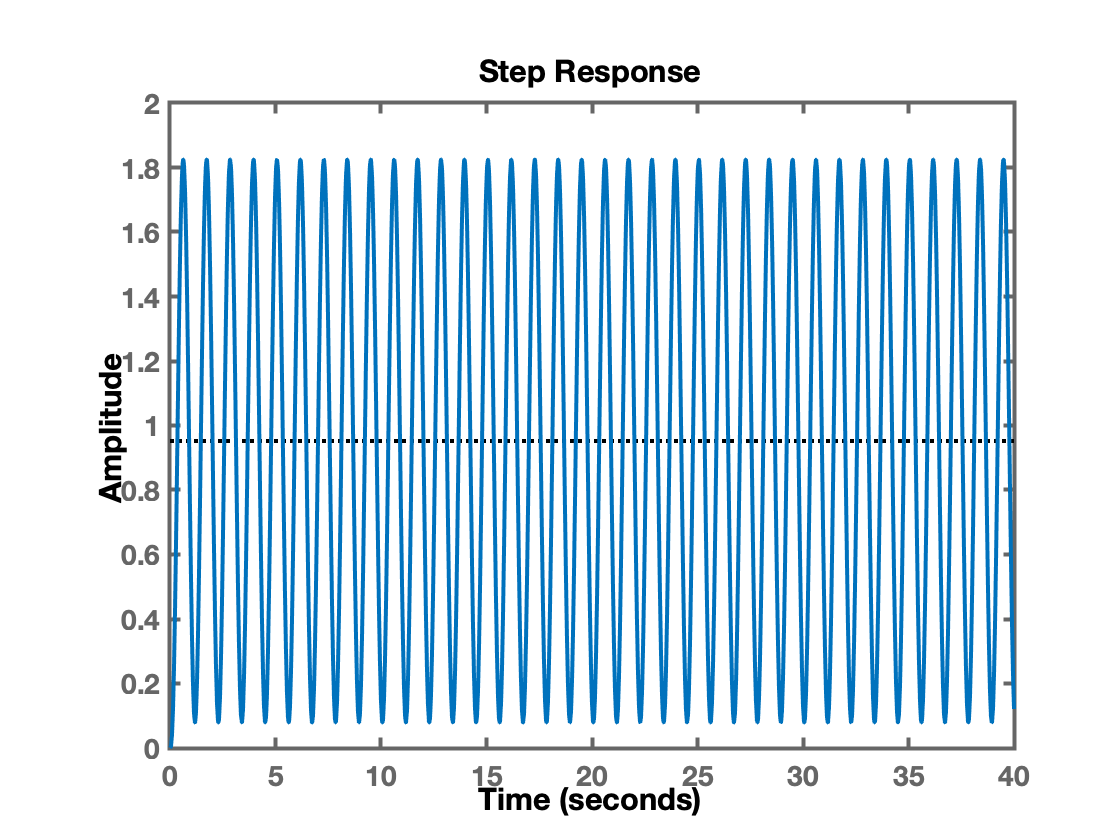
Simulando a malha fechada com diferentes valores para obtemos as seguintes respostas:
 |  |
 |
As figuras anterioes foram obtidas com os seguintes comandos no Matlab:
>> Ku=400;>> ftmf=feedback(Ku*G, 1);>> figure; step(ftmf)>> Ku=380;>> ftmf=feedback(Ku*G, 1);>> figure; step(ftmf)>> Ku=396;>> ftmf=feedback(Ku*G, 1);>> figure; step(ftmf)Perceba-se que trata-se de um método de tentativa e erro que pode demandar certo tempo.
Obs.: O valor exato de pode ser obtido usando-se o método de Routh-Hurwitz.
Notamos que com o sistema assumiu uma oscilação "consistente" (senóide de amplitude constante).
Resta obter os dados do período de oscilação . No Matlab:
>> % Realizando um "zoom" sobre uma parte interessante>> axis([0 12 0 2])O gráfico permite selecionar 2 pontos distantes e inferir o período de oscilação:
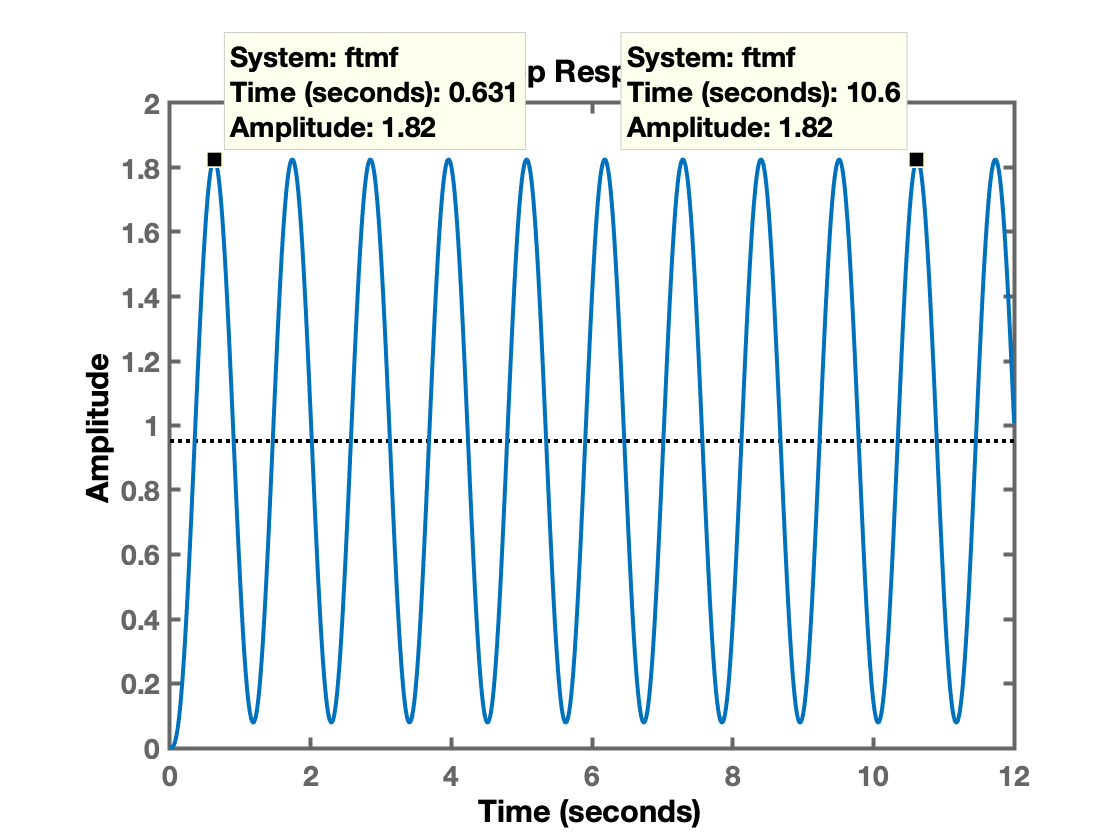
Usando o Matlab podemos determinar :
>> % notamos que entre os pontos selecionados estão 9 ciclos completos>> Tu=(10.6-0.631)/9Tu = 1.1077De posso de e e usando a tabela de Ziegler-Nichols podemos descobrir valores iniciais para os parâmetros do PID:
| Controlador | |||||
|---|---|---|---|---|---|
| PID |
Usando o Matlab novamente:
>> Kc=0.6*KuKc = 237.6000>> Ti=Tu/2Ti = 0.5538>> Td=Tu/8Td = 0.1385E assim nosso PID inicialmente fica:
Simulando no Simulink (arquivo: sintonia_PID_exemplo.slx) resulta em:
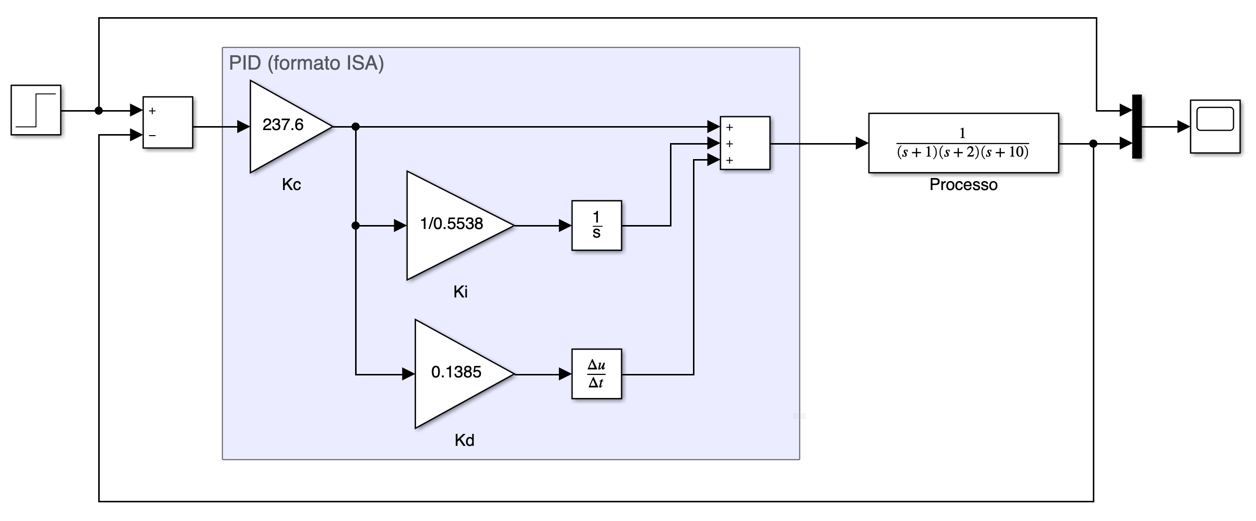
Este diagrama de blocos foi exportado para PNG fazendo:
>> print -r150 -dpng -ssintonia_PID_exemplo sintonia_PID_exemplo.pngO resultado da simulação para 7 segundos pode ser visto na próxima figura:
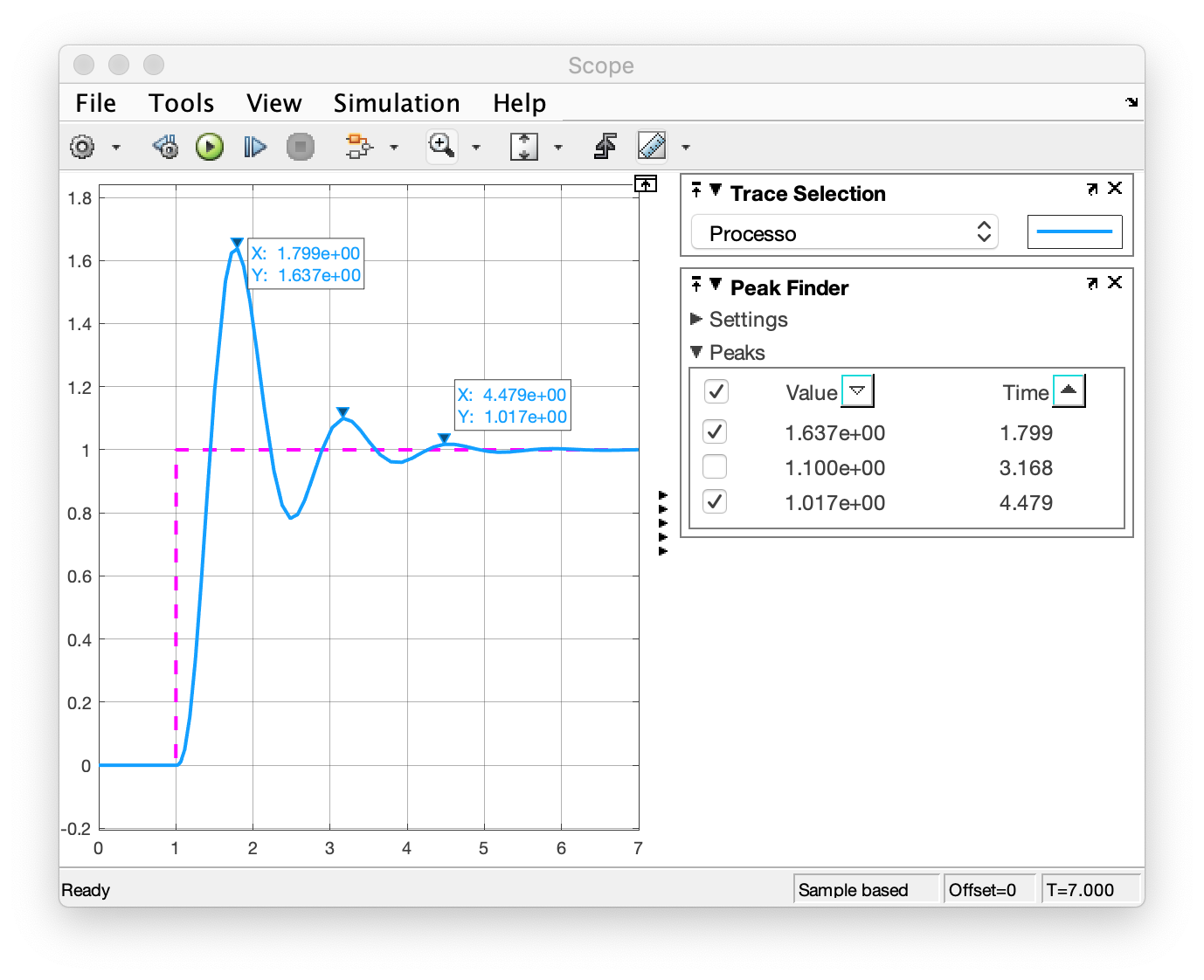
ou seja, nota-se um e (segundos).
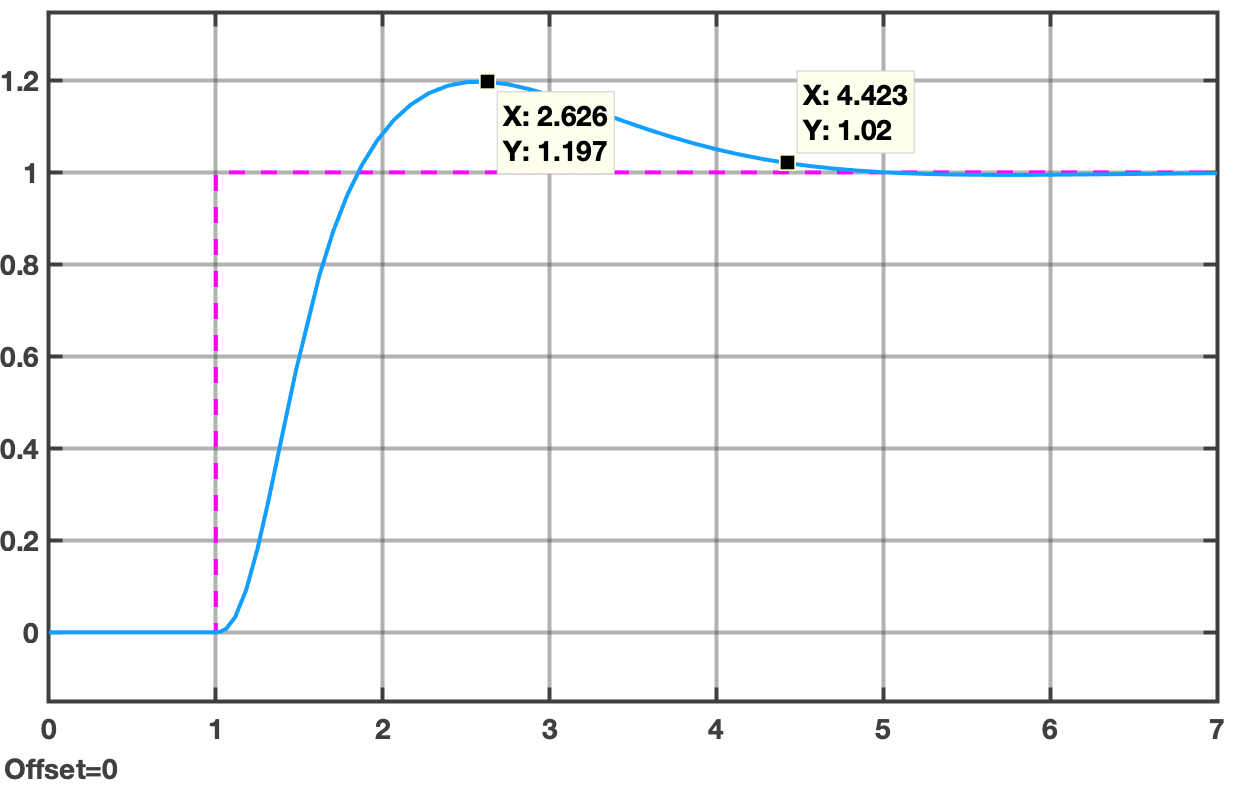
Se faz um necessário um ajuste fino deste PID:
Com os valores:
;
;
.
Foi obtido o seguinte resultado:
Prof. Fernando Passold (Julho/2020)