Controle Automático I
Trabalho: 6) Root Locus
Objetivo: Compreender como o ganho influencia a posição dos pólos em MF (Malha-Fechada).
1) RL de sistema simples
Adapte o script rlsimples.m abaixo para o caso da função transferência (planta) indicada à seguir e entenda como ser origina o RL para um sistema simples como este:
Suponha que este sistema será incorporado numa malha de controle automático com realimentação unitária negativa e que será acrescentando um ganho proporcional, com valor variável . Note que o traçado do RL é formado plotando a forma como os pólos de MF deste sistema "caminham" no plano-se conforme o ganho é variado de valores muito baixo à valores elevados.
A função transferência em MF fica:
A EC(s), equação característica fica:
Quando , resulta: , com raíz (pólo de MF) em: .
O Matlab permite determinar as raízes deste polinômio fazendo:
xxxxxxxxxx>> K = 1; % arbitrando um valor para o ganho K>> EC=[(K+1) (K+5)] % monta o polinômio no MatlabEC = 2 6>> % Ou seja: EC(s)=2s+6 >> roots(EC) % calcula as raízes do polinômio ECans = -3Podemos obter um gráfico de Root Locus simplesmente variando o valor do ganho e plotando o pólo de MF calculado no plano-s.
O script abaixo (rlsimples.m) permite automatizar este processo (adapte a variável EC para o seu caso)
xxxxxxxxxx% rlsimples.m% Determinando faixa de polos em MF, % variando ganho para fig. 4.1 NISE% Fernando Passold, em 01.04.2019K=[0 0.1 0.5 1 1.5 2 4 10 50 100 400 700 1000]; % vetor com valores de ganhou=length(K); % descobre tamanho do vetorfprintf(' K | EC(s)=0 | Polo em (s=)\n');for i=1:u % acessa cada ganho do vetor K EC = [(K(i) + 1) (2*K(i) + 5)]; % monta o polinômio referente à EC(s) polo = roots(EC); % calcula as raízes da EC(s) fprintf('%5.1f | %g s + %g = 0 | %7.2f\n', K(i), EC(1), EC(2), polo); % mostra valoresendEste script gera uma "tabela" com valores. Deverá ser notado como o pólo de MF "caminha" do pólo de MA em , na direção do zero em .
Você pode usar a função logspace() para variar o vetor de ganhos de forma logarítmica:
xxxxxxxxxx>> K=logspace(-1, 3, 20) % varia de 10^{-1} até 10^{3}, 20 pontosK = Columns 1 through 7 0.1 0.16238 0.26367 0.42813 0.69519 1.1288 1.833 Columns 8 through 14 2.9764 4.8329 7.8476 12.743 20.691 33.598 54.556 Columns 15 through 20 88.587 143.84 233.57 379.27 615.85 1000>> help logspace % se quiser entender maisVocê pode plotar a sequencia de pólos de MF executando este outro script em sequência do rlsimples.m:
xxxxxxxxxx% rlsimples2.m% Plota a sequencia de pólos de MF calculados por rlsimples.mu=length(K); % descobre tamanho do vetorfigure;plot([-6 1], [0 0], 'k-') % plota eixo real Xxlabel('Real\{s\}')hold on % próximos gráficos se sobrepões à esteplot([0 0], [-1 1], 'k-') % plota eixo imaginário Yylabel('Imag\{s\}');for i=1:u % acessa cada ganho do vetor K plot(real(polo(i)), imag(polo(i)), 'r+', 'MarkerSize', 18, 'LineWidth', 2); % plota o i-ésimo polo string = num2str(K(i),'%g'); texto = ['K=' string]; recuo = (length(texto)/2)*0.075; text(real(polo(i))-recuo, imag(polo(i))+i*0.05, texto); % acrescenta texto pause(3) % pausa de 3 segundos entre cada pontoendgridaxis([-6 1 -1 1]) % limita região mostradaEm seguida, use o comando locus() do Matlab para obter o gráfico do RL para este sistema. Deve resultar algo do tipo:
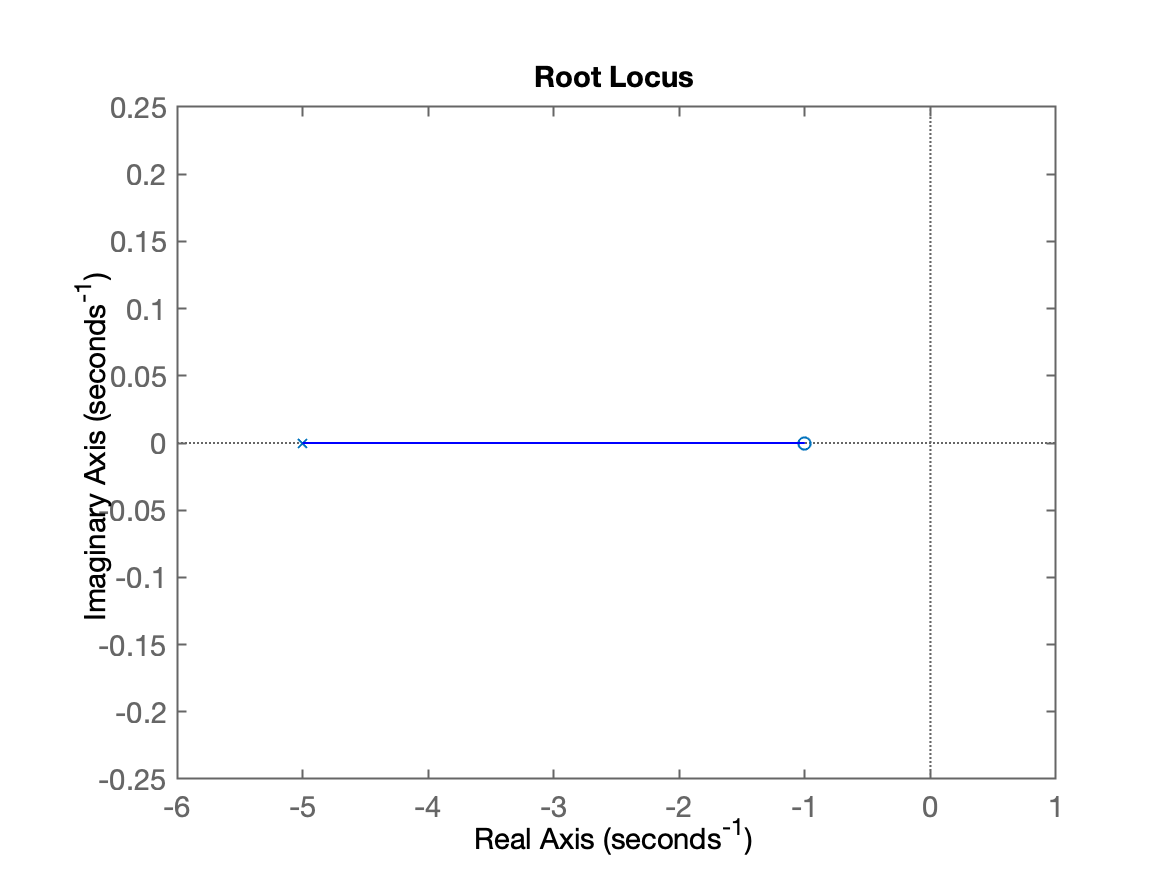
1) RL de sistema de 2a-ordem
Suponha agora que se deseja o RL para o sistema abaixo:
A idéia é gerar uma tabela relacionando ganho (variando) com pólos de MF associados com cada valor de ganho. e depois um gráfico do RL que mostre como a posição dos pólos de MF variam conforme o ganho varia. Deve ser obtido algo semelhante à:
| K | Polo 1 | Polo 2 |
|---|---|---|
| 0.1 | -9.98999 | -0.01001 |
| 0.162378 | -9.98374 | -0.0162642 |
| 0.263665 | -9.97356 | -0.0264364 |
| 0.428133 | -9.957 | -0.0429982 |
| 0.695193 | -9.92999 | -0.0700094 |
| 1.12884 | -9.88581 | -0.114188 |
| 1.83298 | -9.81321 | -0.186787 |
| 2.97635 | -9.69294 | -0.307064 |
| 4.83293 | -9.49078 | -0.509224 |
| 7.8476 | -9.14155 | -0.858454 |
| 12.7427 | -8.50104 | -1.49896 |
| 20.6914 | -7.07572 | -2.92428 |
| 33.5982 | -5 + j2.93227 | -5 - j2.93227 |
| 54.5559 | -5 + j5.43654 | -5 - j5.43654 |
| 88.5867 | -5 + j7.97413 | -5 - j7.97413 |
| 143.845 | -5 + j10.9016 | -5 - j10.9016 |
| 233.572 | -5 + j14.442 | -5 - j14.442 |
| 379.269 | -5 + j18.822 | -5 - j18.822 |
| 615.848 | -5 + j24.3074 | -5 - j24.3074 |
| 1000 | -5 + j31.225 | -5 - j31.225 |
Obs.: A tabela acima foi gerada para a planta: , usando a rotina indicada abaixo rlsimples3.m.
Este caso termina sendo um pouco mais complexo que o caso anterior, porque dependendo do valor do ganho , haverá pólos de MF que são números complexos. Por este motivo, segue o script rlsimples3.m capaz de gerar uma tabela como a mostrada anteriormente.
Obs.: Adapte a rotina para o seu caso. Isto significa que você deve determinar os termos do polinômio da equação característica antes de executar esta rotina e então modificar a linha com a declaração: EC = [1 10 K(index)]; para o seu caso.
xxxxxxxxxx% rlsimples3.m% calcula pólos de MF para sistema de 2a-ordem apenas pólos% Fernando Passold% Nesta caso para a planta:% G(s) = 1/(s(s+10))close all; clear all;G=tf(1,poly([0 -10]));disp('Planta:')zpk(G) % mostra tf da planta em formato mais amigávelfprintf('\n')K=logspace(-1, 3, 20);u=length(K);% Gera texto/tabela no formato markdownfprintf('| K | Polo 1 | Polo 2 |\n');fprintf('| :--- | ---: | ---: |\n');figure;for index=1:u fprintf('| %g | ', K(index)); EC = [1 10 K(index)]; % monta EC(s) (e mostra polin?mio) polo = roots(EC); fprintf('%g ', real(polo(1))); aux=num2str(K(index)); if ~(isreal(polo(1))) % caso de pólos complexos plot(real(polo),imag(polo),'bx','LineWidth',2,'MarkerSize',12) text(real(polo)+.2,imag(polo),aux); aux=abs(imag(polo(1))); fprintf('+ j%g ', aux); else plot(real(polo),[0 0],'bx','LineWidth',2,'MarkerSize',12) text(real(polo)+.2,[0.2 0.2],aux); end fprintf(' | %g ', real(polo(2))); if ~(isreal(polo(1))) fprintf('- j%g ', aux); end if index==1 hold on end fprintf(' |\n');endtitle('Plano-s');xlabel('Real (\sigma)');ylabel('Imag (j\omega)')% compare com RL gerado pelo Matlabfigure; rlocus(G)
3) RLs Diversos vs Ku
Use o Matlab (ou Octave) para: 1) obter o RL para os diferentes sistemas listados à seguir:
a) (sistema de 2a-ordem, só pólos, ganho DC unitário)
b) (sistema de 3a-ordem, só pólos)
c) (sistema similar ao anterior, mas com ganho DC unitário)
d) (sistema de 3a-ordem com 1 zero)
e) (sistema de 3a-ordem com 1 zero no semi-plano direito do plano-s sistema de fase mínima)
f) (sistema de 4a-ordem, só pólos)
g) (modelo de 5a-ordem, simplificado, para controle de altitude de um drone)
Também: 2) Informar o máximo ganho proporcional, ou Ultimate Gain, que pode ser aplicado à cada um dos sistemas; mostre no RL (com auxílio do "data tip") o ponto onde ocorre o ganho máximo; e 3) mostre uma simulação mostrando o resultado em malha-fechada, quando se aplica uma entrada degrau, usando este valor de ganho. Eventualmente o sistema permite , explique estes casos.
Observações:
Não esquecer de fechar a malha com o ganho desejado usando comando
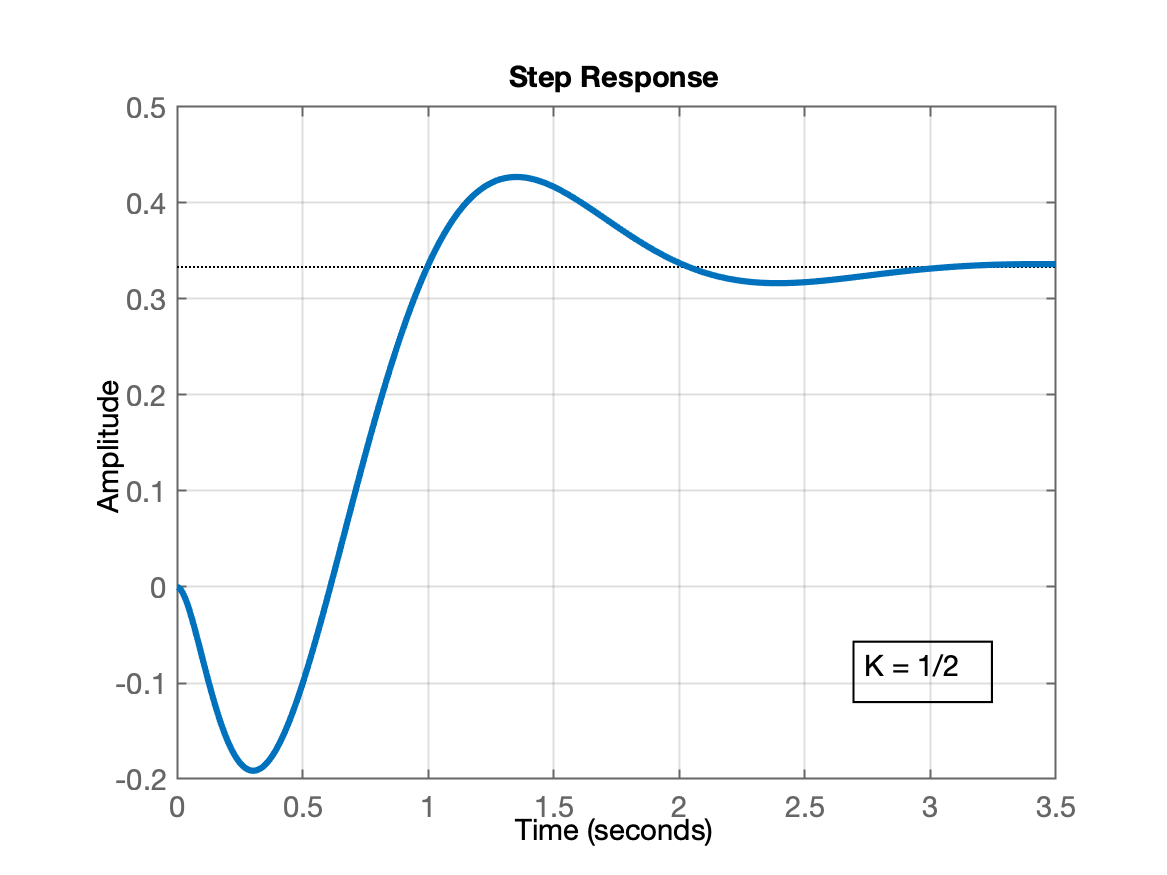
feedback()antes de usar comandostep().O sistema (e), com função transferência: , é do tipo de "sistema de fase mínima", isto é, sua resposta antes de alcançar um valor positivo para uma referência positiva, responde inicialmente com valores negativos. Se você tentar fechar a malha deste sistema com vai resultar na resposta como a mostrada na proxima figura:
Eventualmente para ingressar os dados do denominador da última função transferência você pode usar a funçao
conv()do Matlab:xxxxxxxxxx>> den=conv([1 14 100],[1 3.2 4])den =1 17.2 148.8 376 400>> den=conv(den,[1 20])den =1 37.2 492.8 3352 7920 8000>> G7=tf(800,den);>> zpk(G7)ans =800-----------------------------------------(s+20) (s^2 + 3.2s + 4) (s^2 + 14s + 100)Continuous-time zero/pole/gain model.Ou pode-se imaginar blocos sendo "cascateados" e realizar uma simples multiplicação entre as funções transferência:
xxxxxxxxxx>> bloco1=tf(1,[1 14 100]);>> zpk(bloco1)1-----------------(s^2 + 14s + 100)Continuous-time zero/pole/gain model.>> bloco2=tf(1,[1 3.2 4]);>> zpk(bloco2)1----------------(s^2 + 3.2s + 4)Continuous-time zero/pole/gain model.>> bloco3=tf(1,[1 20])1------s + 20Continuous-time transfer function.>> G7=800*bloco1*bloco2*bloco3;>> zpk(G7)800-----------------------------------------(s+20) (s^2 + 3.2s + 4) (s^2 + 14s + 100)Continuous-time zero/pole/gain model.E na realidade:
- O bloco1 corresponde à dinâmica de rotação (pitch/roll) do drone (sistema de 2a-ordem, com frequência natural de oscilação, rad/s e fator amortecimento, ; dinâmica mais rápida);
- O bloco2 corresponde à dinâmica de translação vertical do drone (também um sistema de 2a-ordem com sua frequência natural de oscilação, rad/s e fator amortecimento, ; dinâmica mais lenta);
- O bloco3 corresponde ao atraso do filtro do sensor de altitude (sistema de 1a-ordem, com rad/s).]
Se sugere o uso do comando
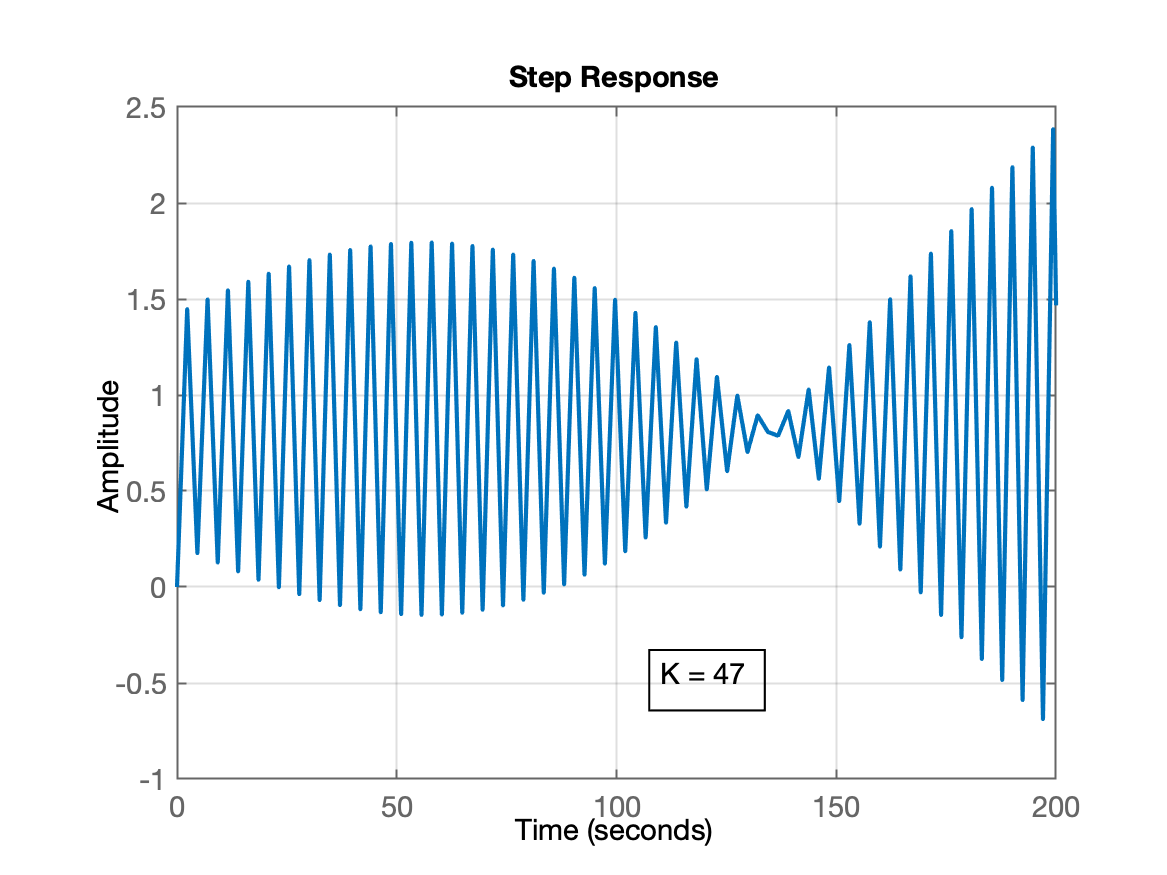
axis([xmim xmax ymin ymax])ouxlim([xmim xmax]), para enquadrar melhor os gráficos, principalmente no caso das respostas ao degrau. No caso do último exemplo, veja a diferença obtida:step(ftmf_G7) step(ftmf_G7); xlim([0 200]) 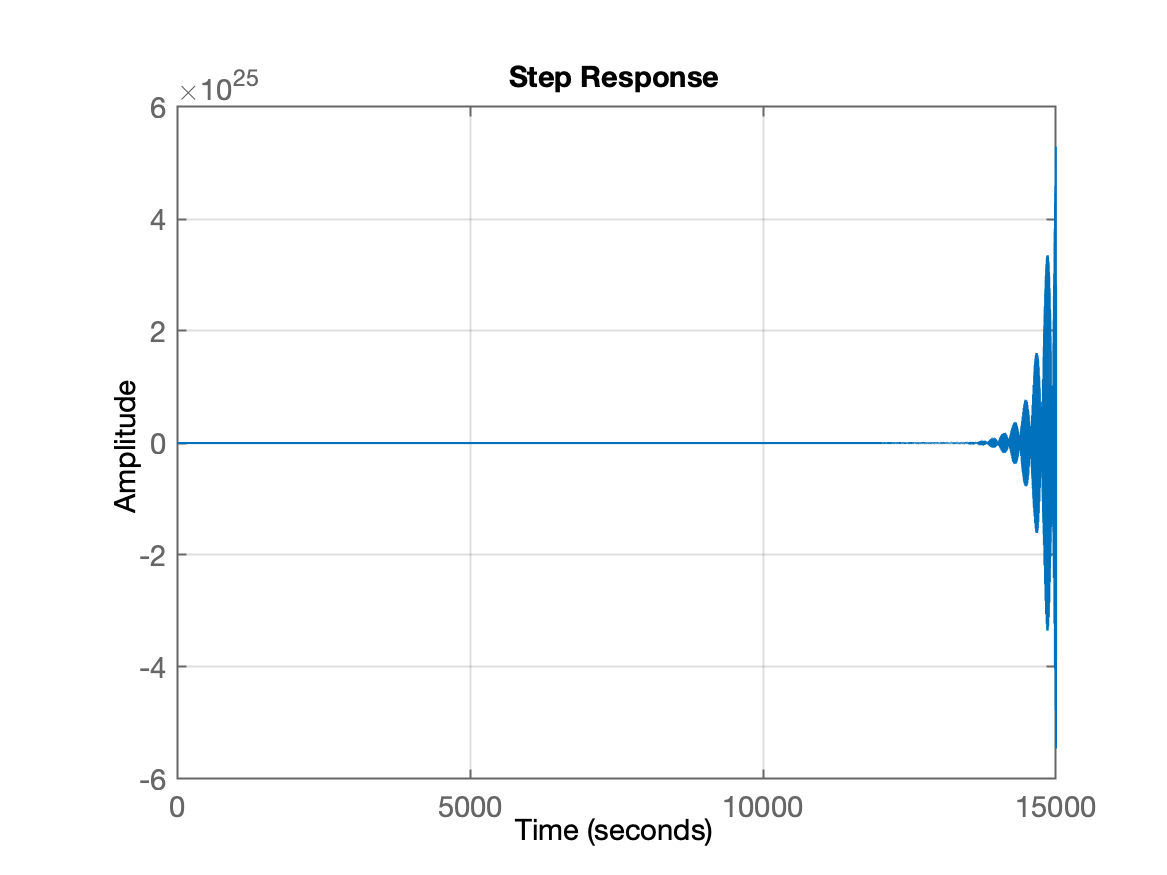
Observação Final
Favor exportar figuras aumentando resolução para 150 dpi, usando tamanho mínimo de fontes = 14 (para as figuras) -- ver: recomendações para salvar gráficos.
Fernando Passold, em 23/05/2025.