Controle Automático I

Trabalho: 5. Respostas temporais de sistemas lineares

Objetivo: Entender como a posição dos pólos afeta a dinâmica de sistemas (1ª e 2ª ordem).

1) Exercícios com pólos reais simples

Para cada sistema abaixo, calcule o tempo de resposta, $t_s$ (tempo de assentamento, settling time) dos mesmos quando submetidos à uma entrada degrau. Mostre este instante de tempo no gráfico obtido$^{[1]}$.

a) $G_1(s)=\dfrac{1}{s+1}$;

b) $G_2(s)=\dfrac{5}{s+5}$;

c) $G_3(s)=\dfrac{15}{s+15}$

A idéia aqui é criar uma figura semelhante a mostrada abaixo, que permite visualizar graficamente e concluir que quanto mais distante um pólo real estiver afastado do eixo $j\omega$, mas rápida será sua resposta:

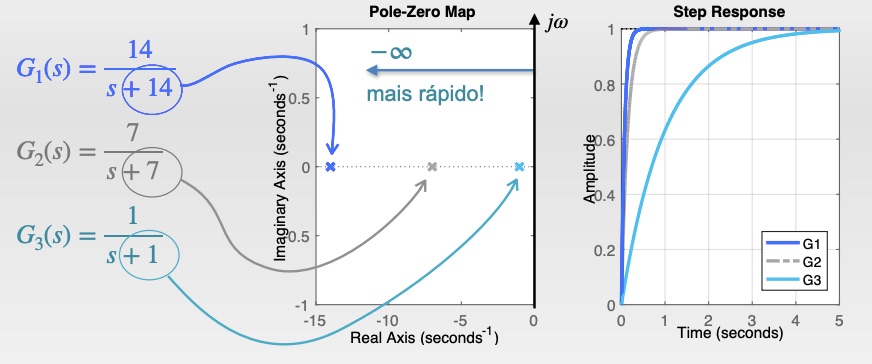
Estime o valor do $t_s$, que corresponde à aproximadamente à 4 vezes a constante de tempo de cada sistema (considerando o critério dos 2% para tempo de assentamento).

$^{[1]}$ Dicas: No Matlab, você pode usar a seguinte sequência de comandos para gerar os gráficos:

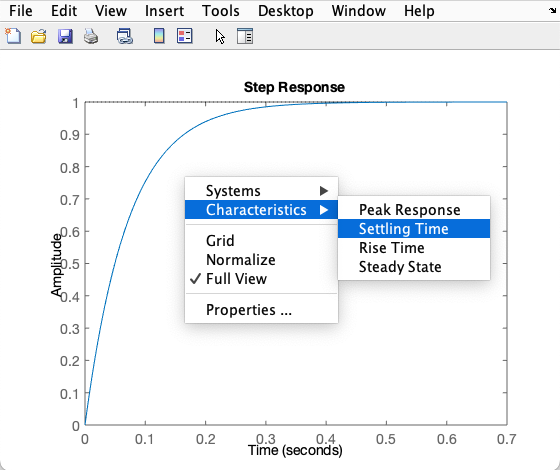
​x
>> G1=tf(14,[1 14])     % ingressa com a transfer function
​
G1 =
 
    14
  ------
  s + 14
 
Continuous-time transfer function.
​
>> figure; pzmap(G1)    % gera o diagrama dos pólos/zeros no plano-s
>> % axis([xmin xmax ymin ymax])
>> axis([-15 0 -1 1])   % "padroniza" área a ser mostrada no gráfico
>> figure; dcgain(G1)   % mostra resposta à entrada degrau
>> axis([0 5 0 1])      % "padroniza" área a ser mostrada neste caso
>> stepinfo(G1)         % mostra informações
        RiseTime: 0.15693
    SettlingTime: 0.27943
     SettlingMin: 0.9045
     SettlingMax: 0.99997
       Overshoot: 0
      Undershoot: 0
            Peak: 0.99997
        PeakTime: 0.75327
>> tau=1/14     % calcula constante de tempo do sistema
tau =
     0.071429
>> ts=4*tau     % preve ts
ts =
      0.28571
>> 

No gráfico gerado pelo comando step() clique com o botão direito do mouse sobre uma área do gráfico para obter o menu com opções para incluir o tempo de assentamento no gráfico (Settling Time):

2) Seja um sistema constituído apenas por pólos reais:

$G(s)=\dfrac{48}{(s+1)(s+4)(s+12)}$

Use a função residue do MATLAB para descobrir o impacto de cada pólo na resposta deste sistema para uma entrada degrau unitário. Mostre uma equação como, com os correspondentes valores numéricos:

$y(t)=R_1 + R_2 e^{-{p_1 t}} + R_3 e^{-{p_2 t}} + R_4 e^{-{p_3} t}$

onde: $y(t)=\mathfrak{L}^{-1}\{ Y(s) \}$; $Y(s)=R(s) \cdot G(s)$; $R(s)=$ transformada de Laplace da entrada degrau; $R_1=$ offset (constante) de amplitude na resposta de $y(t)$ (degrau de certa amplitude); $R_2, R_3, R_4$, correspondem aos resíduos (fatores ponderação) para cada pólo $p_i$ deste sistema.

E obtenha um gráfico semelhante ao mostrado abaixo:

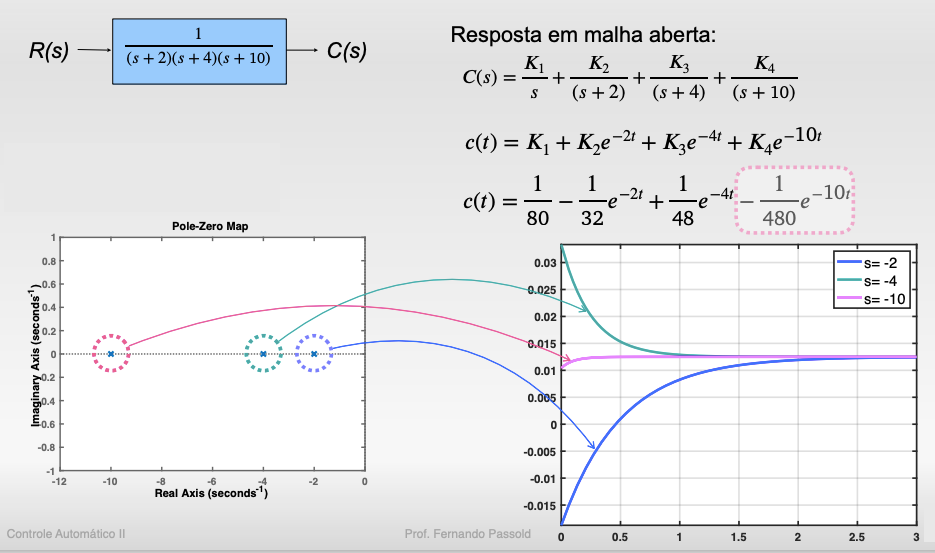
O objetivo aqui é perceber que os pólos mais próximos do eixo $j\omega$ são os que "ditam" a resposta e por isto mesmo são ditos: "pólos dominantes" na resposta. No caso do sistema exemplo acima, os pólos dominantes estão em $s=-2$ e $s=-4$. O pólo localizado em $s=-10$ praticamente não influencia na resposta.

3) Respostas de sistemas de 2a-ordem

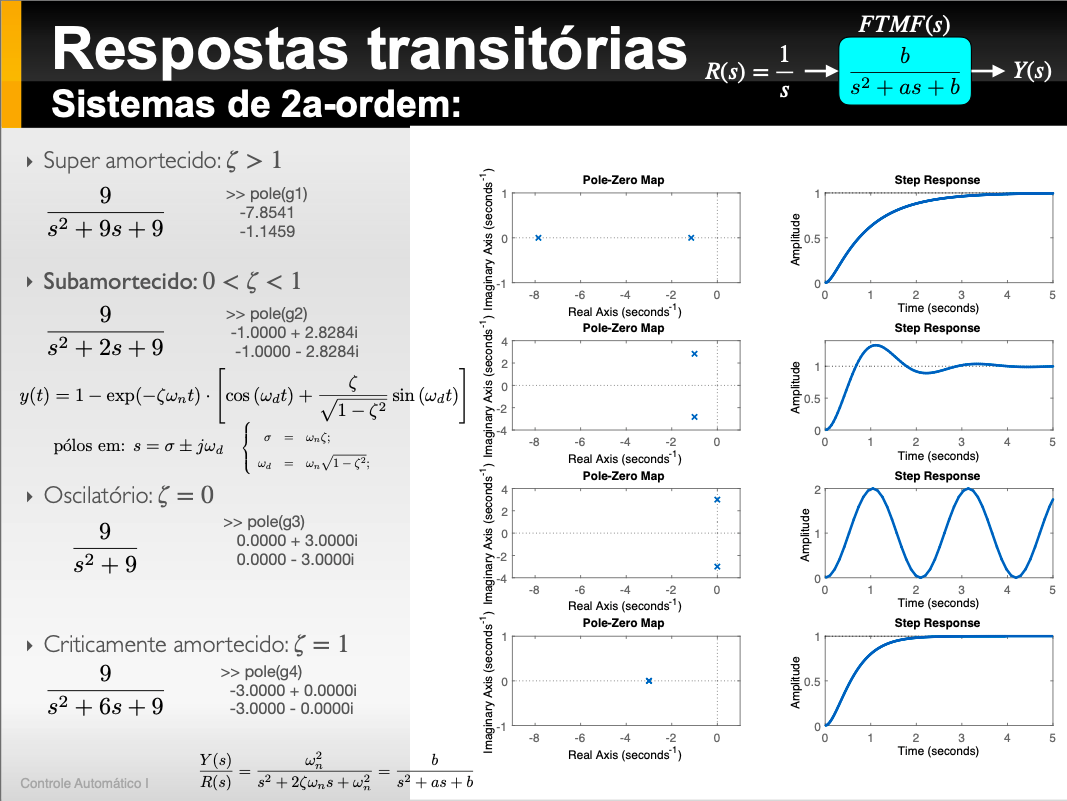
Para cada situação abaixo, mostre sua função transferência, use a função dcgain() para prever o valor final em regime permanente alcançado pelo mesmo (ou $y(\infty)$), mostre o gráfico da resposta à entrada degrau (usando a funçãp step()) e mostre no plano-s a localização destes pólos (usando a função pzmap()). Para os item (a) e (b) calcule a frequência natural, $\omega_n$ e fator de amoertecimento, $\zeta$. Já no caso dos itens (c), (d) e (e) são fornecidos os parâmetros: $\zeta$ (fator de amortecimento) e $\omega_n$ (freq. natural de oscilação), e você deve então descobrir onde estão localizados os pólos de cada uma destes sistemas (são pólos complexos). Será necessário montar a função transferênica, descobrir os pólos de cada sistema, mostrar estes pólos no plano-s (usando pzmap()) e plotar a resposta ao degrau unitário para estes sistemas, e classificar sua resposta em: sistema superamortecido, sistema subamortecido, sistema criticamente amortecido ou sistema oscilatório.

a) Sistema com pólos em: $s=-1$ e $s=-4$;

b) Sistema com pólos em: $s=-2$ e $s=-2$ (pólos duplos);

c) Sistema com: $w_n=2\pi$ (rad/s (ou 1 Hz) e $\zeta=0,2$.

d) Sistema com: $w_n=2\pi$ (rad/s (ou 1 Hz) e $\zeta=0,6$.

e) Sistema com: $w_n=7$ (rad/s) (ou 1,11 Hz) e $\zeta=0$.

Dica: No caso dos sistemas subamortecidos, você pode obter a função transferência fazendo algo como:

xxxxxxxxxx
>> wn =     % completar...
>> zeta =   % deduzir/completar...
>> G=tf(1,[1 2*zeta*wn wn^2])
>> zpk(G)   % mostra a tf num formato mais "amigável"
>> pole(G)  % mostra os pólos da tf
>> pzmap(G) % plota os pólos no plano-s
>> step(G)  % mostra a resposta à entrada degrau.

É esperado que seja gerado algo semelhante à figura abaixo:

4) Respostas de Sistemas de ordem superior

Obtenha figuras similares às mostrada na tabela abaixo, que mostre a resposta à entrada degrau e os pólos de cada sistema no plano-s. Sejam os sistemas:

a) $G(s)=\dfrac{200}{(s^2+4s+20)(s+10)}$;

b) $G(s)=\dfrac{60}{(s^2+4s+20)(s+3)}$;

c) $G(s)=\dfrac{10}{(s^2+4s+20)(s+1/2)}$;

Obsservações:

1. Compare a resposta ao degrau destes sistemas com o sistema "base", constituído apenas por $G(s)=\dfrac{20}{(s^2+4s+20)}$ (apenas os pólos complexos).
2. Tente montar uma "tabela" resumo com figuras, como a mostrada à seguir:
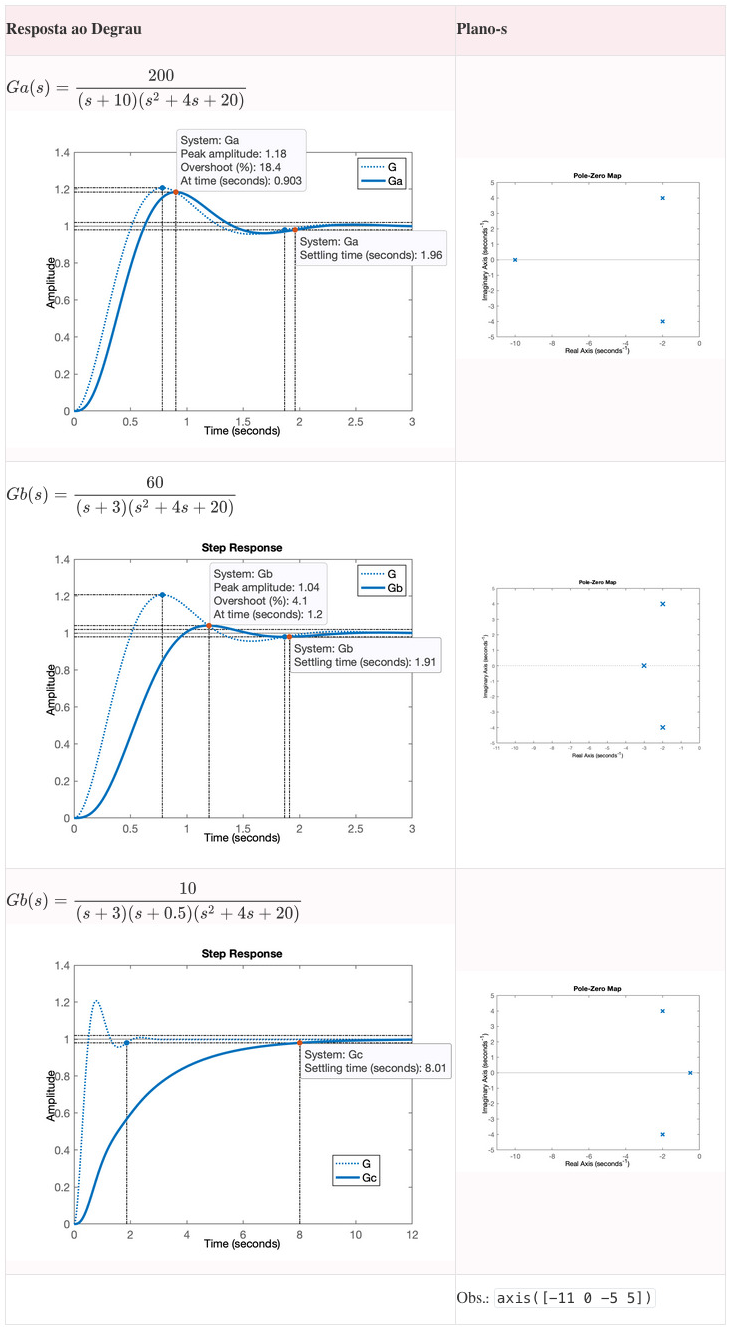
3. Você deve perceber o impacto do pólo real versus os pólos complexos presentes no sistema. Deve perceber que quanto mais longe e na direção de $s \to -\infty$ o pólo real estiver, menor será seu impacto no sistema e o sistema responde como se fosse um simples sistema de 2a-ordem. A medida que o pólo real se aproxima dos pólos complexos a resposta de um sistema de 2a-ordem baseada apenas nos pólos complexos é "distorcida" pelo pólo real. E eventualmente este pólo real pode dominar na resposta deste sistema.
4. Note que o tempo de assentamento alcançado apenas pelos pólos reais da última função transferência, quando: G3=tf(0.5,[1 0.5]); figure; step(G3); stepinfo(G3, G):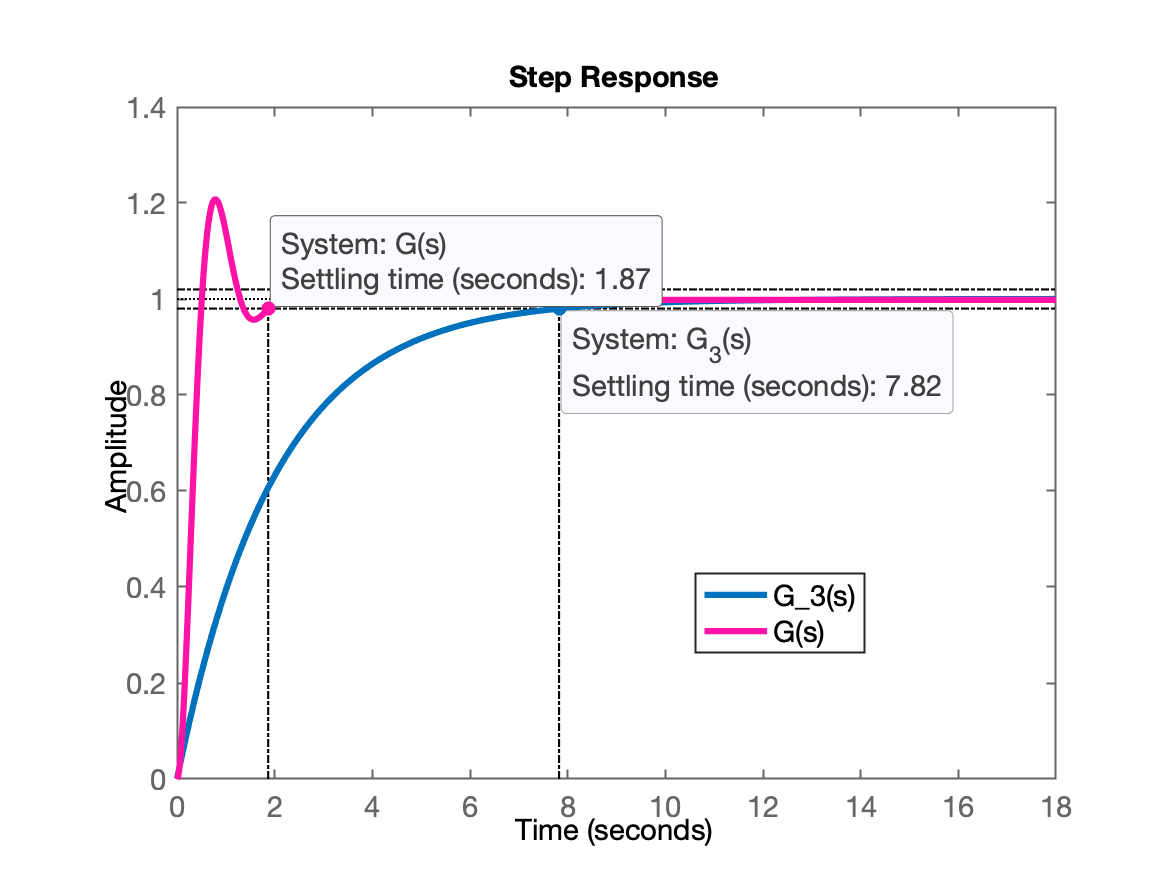

Fim

Fernando Passold, em 23/05/2025