Trabalho sobre Série de Fourier

Sugere-se ler os tópicos abaixo listados:

• Série de Fourier (teoria);
• Demo (com simulações) do MIT: FOURIER SERIES DEMO (acessado em 13/06/2024);
• Math's Fun Advanced >> Fourier Series;
• Matlab fácil (tutorial).

Itens do trabalho

1. Usando Série de Fourier, sintetize uma Onda Quadrada oscilando à 20 Hz, com aplitude de 1,0 Vpp, mas:

   a) Até sua 5a-harmônica (quinto componente não nulo);

   b) Até sua 25a-harmônica (vigésimo quinto componente não nulo).

   Apresente uma figura/tabela que compare lado à lado os gráficos geradas para os itens (a) e (b).

   Obs.: Os itens (a) e (b) devem mostrar um diagrama no tempo da forma de onda resultante e o espectro da onda (somente parte de magnitudes absolutas), além de uma tabela mostrando as amplitudes de cada harmônica.

    

2. Simule uma onda quadrada que oscila à 20 Hz @ 1,0 Vpp, passando por um filtro Butterworth passa-baixas de 4a-ordem com frequência de corte em $f_c=$ 50 Hz.

   Apresente um diagrama no tempo mostrado na mesma figura a onda quadrada original e o sinal filtrado. Deve resultar algo semelhante à:

   

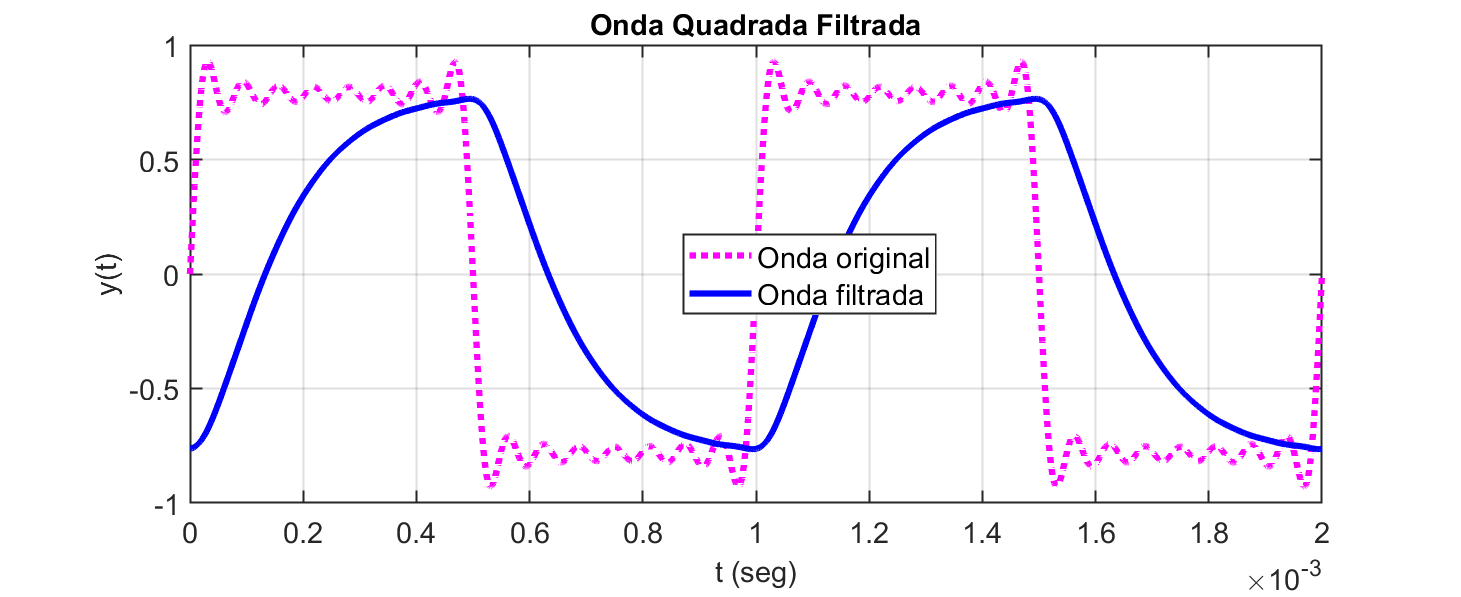
   Obs.: a figura anterior representa uma onda quadrada que oscila à 2 Hz, passando por filtro passa baixas com frequencia de corte em 2 Hz.

   Mostre também o espectro original e filtrado da onda quadrada. Algo como:

   

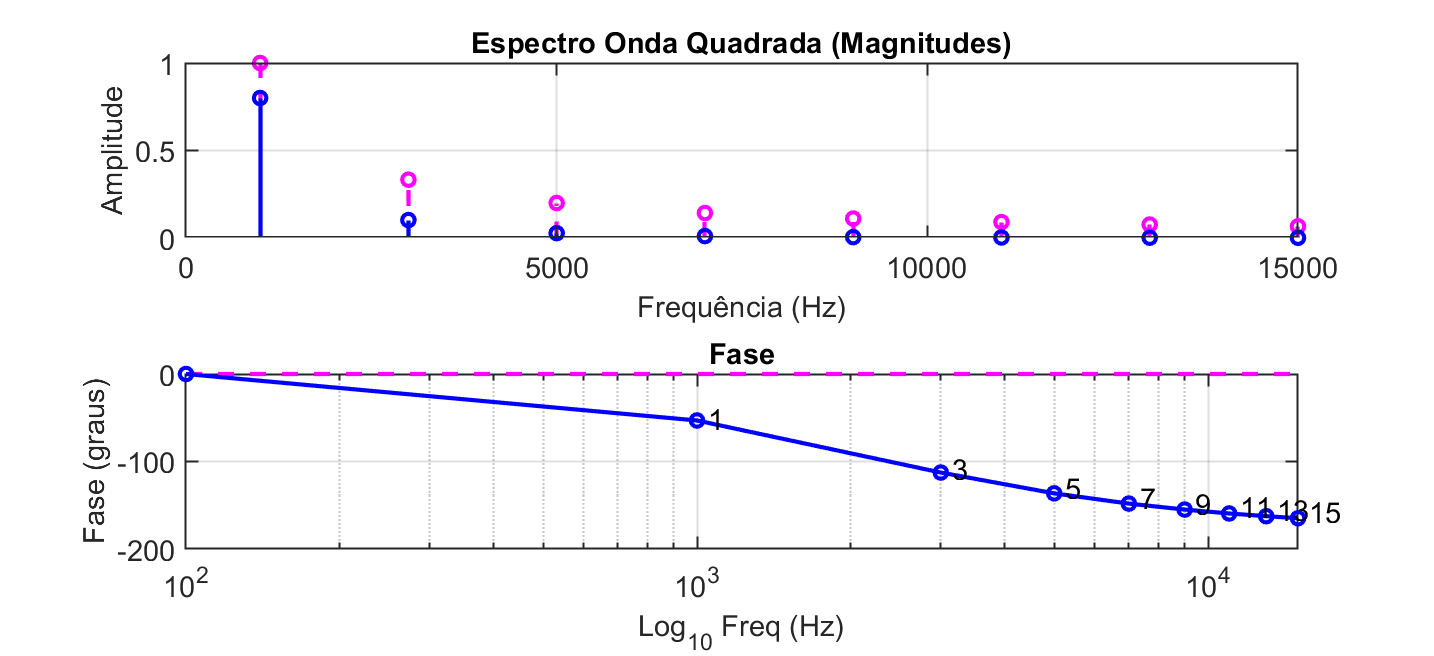
   Na figura acima, a onda quadrada oscila à 1 KHz e passa por filtro passa-baixas com frequencia de corte em 2 KHz, tendo sido considerada até a 15a-harmônica. A curva em rosa corresponde ao espectro orignal da onda e a curva em azul, ao espectro da onda filtrada.

    

   Obs.: Use os valores levantados no item (1 (b)) anterior, isto é, sintetize a onda quadrada até sua 25a-harmônica.

    

O item (1) têm peso de 40% e o item (2) têm peso de 60%.

Anexos

i. Síntese de Onda Senoidal

Uma onda senoidal oscilando à 1 Hz @ 1,0 Vpp pode ser simulada fazendo-se:

$x(t)=1,0 \cdot \sin{(2\pi \cdot t \cdot 1,0)}$.

Usando a função fplot():

xxxxxxxxxx
>> fplot(@(t) 1*sin(2*pi*1*t), [0 2])
>> grid

ii. Síntese de Sinal Composto

Suponha agora que o sinal que queremos reproduzir no tempo seja composto por 2 senóides:

$x(t)=\underbrace{\sin{(2\pi \cdot t \cdot 1)}}_{x_1(t)} + \underbrace{\dfrac{1}{4} \cdot \sin{(2\pi \cdot t \cdot 4 - 45^o)}}_{x_2(t)}$

ou sejam, uma senóide, $x_1(t)$, de 1 Hz @ 1,0 Vpp e outra senóide, $x_2(t)$, oscilando à 4 Hz @ 0,25 Vpp, defasada de $45^o$ (inicia atrasada).

Usando fplot() ficaria:

xxxxxxxxxx
>> fplot(@(t) 1*sin(2*pi*1*t) + 0.25*sin(4*2*pi*1*t - pi/4), [0 2])
>> grid

Outra opção

Provavelmente será necessário criar um vetor tempo, $t$ e vetores para os sinas $x_1(t)$, $x_2(t)$ e $x(t)=x_1(t)+x_2(t)$ para poder resolver os itens deste trabalho.

Devemos gerar o vetor $t$ usando um "passo" ou fator incremental bastante baixo para evitar que apareçam distorções no traçado da onda dependendo da maior frequênica de interesse. Se sugere, "amostrar" o vetor tempo usando um incremente 50 vezes menor que o menor período de tempo da onda mais rápida. Neste caso, $f_{max}=$ 3 Hz, então $\Delta t=(1/3)*(1/50)=0,00667$ segundos.

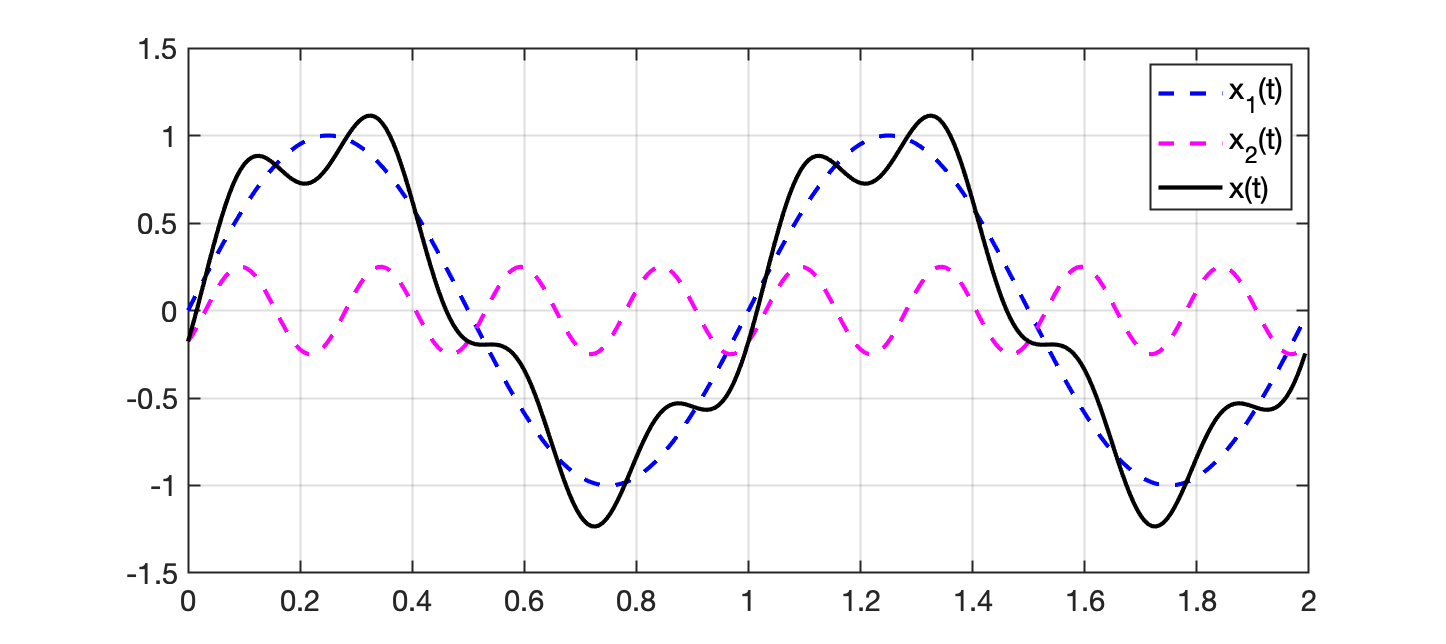
O código para sintetizar estas ondas, de forma a visualizar até 2 ciclos do sinal de 1 Hz, ficaria então:

xxxxxxxxxx
>> T=1/3            % período de tempo da onda mais rápida (3 Hz)
T =
      0.33333
>> dt=T/50          % "Delta T", reduzindo em 50 vezes (50 pontos na onda de 3 Hz)
dt =
    0.0066667
>> t=0:dt:2*1/1-dt; % gerando vetor t incremento dt, 2 ciclos em 1 Hz
>> size(t)          % apenas verificando tamanho do vetor gerado
ans =
     1   300
>> x1=1*sin(2*pi*1*t);              % gerando sinal x1(t)
>> x2=(1/4)*sin(2*pi*4*t-pi/4);     % gerando sinal x2(t)
>> x=x1+x2;                         % compondo sinal x(t)
>> whos                             % conferindo variáveis e tamanhos
  Name         Size             Bytes  Class                Attributes
​
  T            1x1                  8  double                         
  ans          1x2                 16  double                         
  dt           1x1                  8  double                         
  t            1x300             2400  double                         
  x            1x300             2400  double                         
  x1           1x300             2400  double                         
  x2           1x300             2400  double                         
​
>> plot(t,x1,'b--', t,x2,'m--', t,x,'k-')
>> legend('x_1(t)', 'x_2(t)', 'x(t)')   

E o resultado seria algo como:

iii. Calculo Filtro Butterworth

O Matlab/Ocatve facilita o cálculo da expressão associada com um filtro Butterworth, usando-se a função butter():

xxxxxxxxxx
>> help butter
 butter Butterworth digital and analog filter design.
    [B,A] = butter(N,Wn) designs an Nth order lowpass digital
    Butterworth filter and returns the filter coefficients in length
    N+1 vectors B (numerator) and A (denominator). The coefficients
    are listed in descending powers of z. The cutoff frequency
    Wn must be 0.0 < Wn < 1.0, with 1.0 corresponding to
    half the sample rate.
    ...
        butter(N,Wn,'s'), butter(N,Wn,'high','s') and butter(N,Wn,'stop','s')
    design analog Butterworth filters.  In this case, Wn is in [rad/s]
    and it can be greater than 1.0.
 
    % Example 1:
    %   For data sampled at 1000 Hz, design a 9th-order highpass
    %   Butterworth filter with cutoff frequency of 300Hz.
 
    Wn = 300/500;                   % Normalized cutoff frequency        
    [z,p,k] = butter(9,Wn,'high');  % Butterworth filter
    [sos] = zp2sos(z,p,k);          % Convert to SOS form
    h = fvtool(sos);                % Plot magnitude response
 
    % Example 2:
    %   Design a 4th-order butterworth band-pass filter which passes
    %   frequencies between 0.15 and 0.3.
 
    [b,a]=butter(2,[.15,.3]);        % Bandpass digital filter design
    h = fvtool(b,a);                 % Visualize filter
 
    See also buttord, besself, cheby1, cheby2, ellip, freqz,
    filter, designfilt.
​
    Documentation for butter
​
>> 

No caso deste trabalho, se faz necessário descobrir a equação deste filtro, passa-baixas, analógico, com frequênica de corte de 50 Hz, então:

xxxxxxxxxx
>> wn=2*pi*50   % calculando freq. de corte em rad/s
wn =
       314.16
>> [b, a] = butter(4, wn, 's')  % calculando coeficientes do filtro (analógico)
b =
            0            0            0            0   9.7409e+09
a =
            1       820.94   3.3697e+05   8.1023e+07   9.7409e+09
>> H=tf(b,a)    % montrando transfer function
H =
                        9.741e09
  -----------------------------------------------------
  s^4 + 820.9 s^3 + 3.37e05 s^2 + 8.102e07 s + 9.741e09
 
Continuous-time transfer function.
​
>> zpk(H)   % apresentando transfer function em formato mais "amigável"
 
                     9.7409e+09
  -------------------------------------------------
  (s^2 + 580.5s + 9.87e04) (s^2 + 240.4s + 9.87e04)
 
Continuous-time zero/pole/gain model.
​
>> pole(H)
      -120.22 +     290.25i
      -120.22 -     290.25i
      -290.25 +     120.22i
      -290.25 -     120.22i
>> figure; rlocus(H)
>> dcgain(H)
ans =
     1
>> % ganho unitário significa que este filtro não atenua sinal abaixo da fc.
>> figure; handler=bodeplot(H); % plotando Diagrama de Bode
>> setoptions(handler,'FreqUnits','Hz')
>> grid
>> setoptions(handler, 'FreqScale','log')

Note que este filtro possui um par de pólos complexos em $s=-120,22 \pm j\,290,25$ e outro par em $s=-290,25 \pm j\,120,22$.

O diagrama de Bode deste filtro rende:

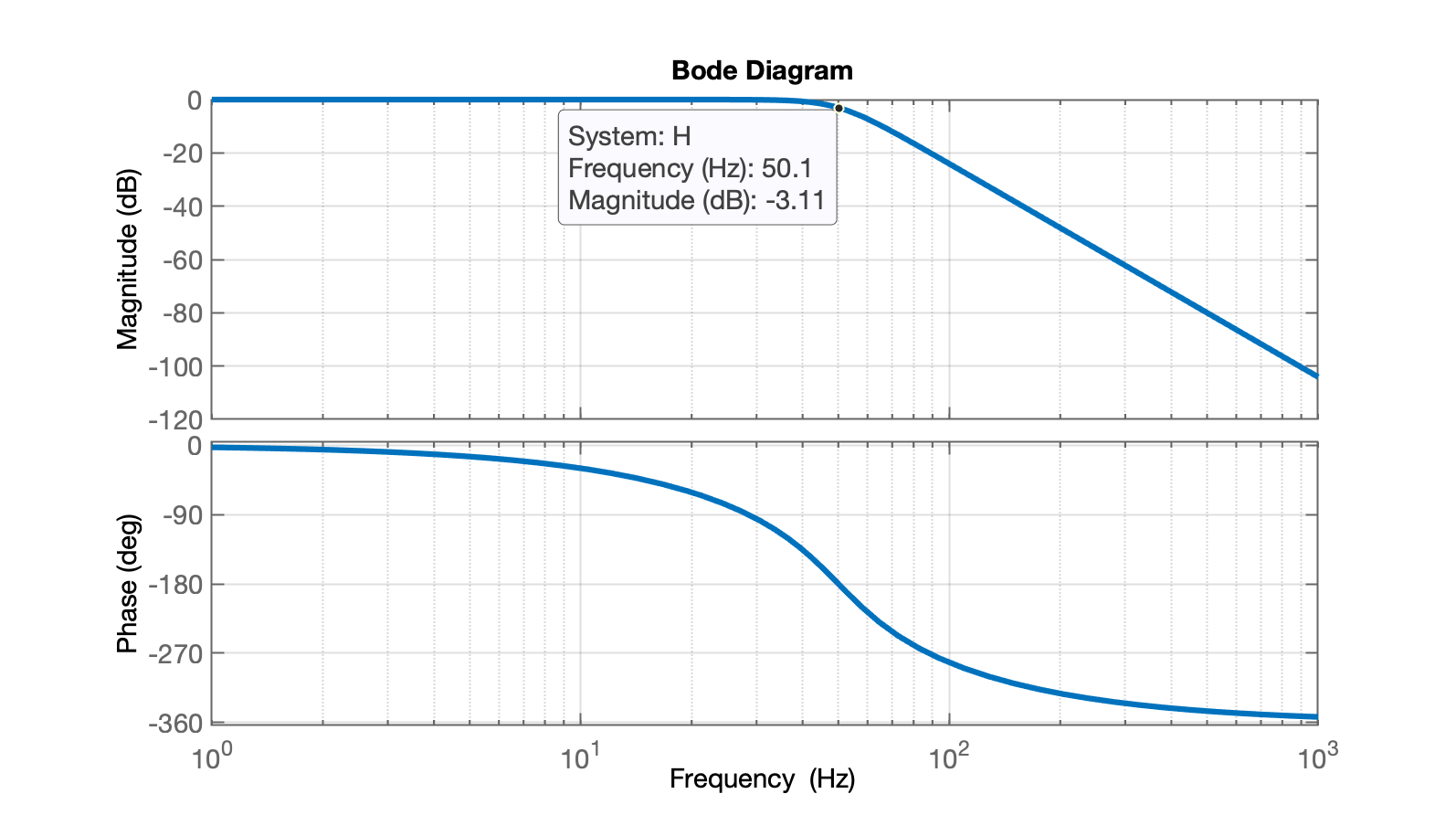
iii. Script para sintetizar onda Quadrada

Segue onda_quadrada_fourier.m usado para sintetizar uma onda quadrada usando série de Fourier:

% onda_quadrada_fourier.m
% Sintetizando onda quadrada
% Fernando Passold, em 17/06/2022
​
clear freq G G_dB t y % evitar problemas se re-executar script
​
disp('Sintese de Onda Quadrada usando Série de Fourier');
f=input('Frequencia da onda quadrada (Hz)? ');
hh=input('Quantos harmonicas para a onda quadrada? ');
n=floor(hh/2)+1; % quantidade de termos da série a serem gerados
​
T=1/f; % periodo da onda quadrada
fs=f*50*20; % freq. "amostragem" onda quadrada (p/efeitos síntese gráficos)
TT=1/fs;
ciclos=2*T; % número de ciclos plotados da onda quadrada
​
t=0:TT:ciclos; % forma vetor tempo
u=length(t); % numero de pontos
for k=1:u   % varrendo vetor tempo
    sum = 0;
    for h=1:n
        termo=2*h-1; % No. da harmônica.
        freq(h)=f*termo; % frequencia da harmonica h
        G(h)=1/termo; % amplitude da harmonica h
        G_dB(h)=20*log10(G(h));
        sum = sum + G(h)*sin(2*pi*freq(h)*t(k));
    end
    y(k)=sum;
end
figure;
plot(t,y);
grid
texto=num2str(termo);
title(['Onda Quadrada (até ' texto '^a harmônica)']);
xlabel('t (seg)');
ylabel('y(t)');
​
% Espectro da onda quadrada gerada
figure;
stem(freq, G); % note que são "impulsos" em freq's ímpares
title('Espectro Onda Quadrada');
xlabel('Frequência (Hz)');
ylabel('Amplitude');
grid
​
figure;
stem(freq, G_dB); % note que são "impulsos" em freq's ímpares
title('Espectro Onda Quadrada');
xlabel('Log_{10}(Freq) (Hz)');
ylabel('20*Log_{10}(Amplitude) (dB)');
set(gca, 'XScale', 'log')
grid

iv. Script para considerar um filtro passa-baixas de 2a-ordem

Segue código exemplo FPB2a_ordem.m usado para computar impacto de um filtro de 2a-ordem Butterworth para certo sinal de entrada. Este script assume que você executou antes onda_quadrada_fourier.m.

xxxxxxxxxx
% FPB2a_ordem.m
% Sintetizando Filtro Passa Baixas (passivo) de 2a-ordem
% Este filtro é resultado do cascateamento em série de 2 filtros de
% 1a-ordem do tipo:
%   H(s)=wc/(s+wc)
% o que resulta, num filtro de 2a-ordem com:
% Magnitude:
%   |H(jw)|= wc^2/sqrt[(wc^2-w^2)^2+(2*wc*w)^2]
%   /angle G(jw) = atan2(2*wc*w, wc^2-w^2)
% Entrada:
% freq = vetor com frequencias que devem ter calculadas |G(jw)| /angle
% Obs: dado anterior gerado usando 'onda_quadrada_fourier.m' (executar
% antes).
% Saída gerada:
% wc = freq de corte do filtro em rad/s
% Tabela relacionando freq x ganho x defasagem
%
% Fernando Passold, em 18/06/2022
​
clear Mag Phase % evitar problemas se re-executar script
​
fc=input('Freq. de corte do Filtro PB (Hz)? ');
u=length(freq); % elementos presentes dentro vetor freq
wc=2*pi*fc;
​
% gerando tabela na tela em formato compatível MarkDown (table)
disp('Comportamento do Filtro com:')
fprintf('freq de corte, fc = %g Hz', fc)
fprintf(' (%g rad/s)\n\n', wc)
%disp('\begin{tabular}{rrrr} \hline')
disp('| Freq | Amplitude | Amplitude | Defasagem |')
disp('| (Hz) | Original | Original (dB) | (graus) |')
disp('| ---: | ---: | ---: | ---: |')
​
for k=1:u % varre freq's desejadas
    w = 2*pi*freq(k); % freq em rad/s
    Re = wc*wc - w*w;
    Im = 2*wc*w;
    Mag(k) = (wc*wc)/sqrt( Re*Re + Im*Im ); % ganho absoluto
    Phase(k) = -atan2( Im, Re ); % em rad/s
    fprintf('| %g |', freq(k));
    fprintf(' %g |', Mag(k));
    fprintf(' %g dB |', 20*log10(Mag(k)));
    fprintf(' %gº |\n', Phase(k)*180/pi); % valor em graus
end
% disp(' \hline')
% disp('\end{tabular}')
disp(' ');

Este script gera uma tabela compatível com Markdown na janela comandos. Algo como:

xxxxxxxxxx
>> FPB2a_ordem
>> Freq. de corte do Filtro PB (Hz)? 300
>> Comportamento do Filtro com:
>> freq de corte, fc = 300 Hz (1884.96 rad/s)
​
| Freq | Amplitude | Amplitude     | Defasagem |
| (Hz) |  Original | Original (dB) |   (graus) |
| ---: | --------: | ------------: | --------: |
|  100 |       0.9 |   -0.91515 dB | -36.8699º |
|  300 |       0.5 |    -6.0206 dB |      -90º |
|  500 |  0.264706 |   -11.5447 dB | -118.072º |
|  700 |  0.155172 |   -16.1837 dB | -133.603º |
|  900 |       0.1 |        -20 dB |  -143.13º |
| 1100 | 0.0692308 |    -23.194 dB |  -149.49º |

Obs.: Este script deverá ser adaptado para o filtro Butterworth de 4a-ordem objetivo deste trabalho.

v. Adaptando script anterior para FPB 4a-ordem

A parte do código FPB2a_ordem.m(do filtro de 2a-ordem) que computou magnitude e fase é:

xxxxxxxxxx
for k=1:u % varre freq's desejadas
    w = 2*pi*freq(k); % freq em rad/s
    Re = wc*wc - w*w;
    Im = 2*wc*w;
    Mag(k) = (wc*wc)/sqrt( Re*Re + Im*Im ); % ganho absoluto
    Phase(k) = -atan2( Im, Re ); % em rad/s
    fprintf('| %g |', freq(k));
    fprintf(' %g |', Mag(k));
    fprintf(' %g dB |', 20*log10(Mag(k)));
    fprintf(' %gº |\n', Phase(k)*180/pi); % valor em graus
end

e considerou equações definidas para filtro Butterworth passa-baixas de 2a-ordem:

$H(s)=\dfrac{w_c^2}{(s+w_c^2)}=\dfrac{w_c^2}{s^2+2 w_c s + w_c^2}$

$H(jw)=\dfrac{w_c^2}{(jw+w_c)^2}=\dfrac{w_c^2}{(w_c^2-w^2)+j2w_c w}$

$\vert H(jw) \vert = w_c^2/\sqrt{(w_c^2-w^2)^2+(2w_c w)^2}$

$\vert H(jw) \vert =w_c^2/\sqrt{4w^2 w_c^2 + (w^2 - w_c^2)^2}$

$\angle{G(jw)} = -tan^{-1}\left( \dfrac{2w_c w}{w_c^2 - w^2} \right)$

Porém, para este trabalho deve ser considerado um filtro de 4a-ordem.

Se você sabe a equação deste filtro, pode substituir o $s$ na equação do mesmo, pelos valores de $s=j \omega$ na frequênica $\omega$ (em rad/s) sendo considerada (lembrar que o Matlab é capaz de realizar operações matemáticas sobre números complexos).

Então... No caso do filtro de 4a-ordem:

$H(s)=\dfrac{9.7409e+09}{(s^2 + 580.5s + 9.87e04) (s^2 + 240.4s + 9.87e04)}$

Ou:

$H(s)=\dfrac{9.741e09}{s^4 + 820.9 s^3 + 3.37e05 s^2 + 8.102e07 s + 9.741e09}$

Se você encontrou os parâmetros deste filtro usando o Anexo iii (anterior), deve notar que está de posse dos coeficientes $a$ (denominador) e $b$ (numerador) deste filtro:

>> a
a =
            1       820.94   3.3697e+05   8.1023e+07   9.7409e+09
>> b
b =
            0            0            0            0   9.7409e+09

Então note, podemos calcular o ganho e defasagem gerados pelo filtro em determinada frequencia fazendo-se:

xxxxxxxxxx
>> freq=50;
>> w=2*pi*freq          % freq convertida para rad/s
w =
       314.16
>> jw=j*w               % criando a variável complexa associada com jw na freq. desejada
jw =
            0 +     314.16i
>> num=polyval(b, jw)   % substituindo jw no polinômio do numerador de H(s)
num =
   9.7409e+09
>> den=polyval(a, jw)   % substituindo jw no polinômio do denominador de H(s)
den =
  -1.3776e+10 + 4.6813e-06i
>> mag=abs(num/den)     % calculando o módulo em valores absolutos
mag =
      0.70711
>> mag_db=20*log10(mag)
mag_db =
      -3.0103
>> phase=angle(num/den) % calculando ângulo de número complexo (em radianos)
phase =
      -3.1416      
>> phase_deg=phase*180/pi   % defasagem em graus
phase_deg =
  -180
>>       

Note que os resultados obtidos anteriormente estão dentro do esperado na frequência de corte para este filtro em 50 Hz.

Adaptando-se estes cálculos no laço FOR que varia a frequência na qual o filtro deve ser aplicado, variável freq(k), basta fazer algo como:

xxxxxxxxxx
wc=2*pi*50;                     % freq. de corte do filtro em rad/s
[b, a] = butter(4, wc, 's');    % calculando os coeficientes a e b do FPB Butterworth de 4a-ordem
% H(s) = N(s)/D(s)
% N(s) = polinômio definido por b
% D(s) = polinômio definido por a
H=tf(b,a);  % variável H é opcional
disp('Função transferência do filtro:')
zpk(H)
​
for k=1:u               % varre freq's desejadas
    w = 2*pi*freq(k);   % freq em rad/s
    jw = j*w;                   % gerando a freq. complexa
    % Note, a linha acima pode produzir erro se por acaso já existe alguma variável `j`
    % sendo usada no Matlab antes deste código. Neste caso, mudar `j` para `i` ou
    % rever forma de uso do Matlab, para evitar variáveis `i` e `j`.
    num = polyval(b, jw);       % resolvendo N(jw) para o H(s)
    den = polyval(a, jw);       % resolvendo D(jw) para o H(s)
    Mag(k) = abs(num/den);      % ganho absoluto na freq(k)
    Phase(k) = angle(num/den);  % defasagem em rad/s na freq(k)
    fprintf('| %g |', freq(k));
    fprintf(' %g |', Mag(k));
    fprintf(' %g dB |', 20*log10(Mag(k))); % valor em dB
    fprintf(' %gº |\n', Phase(k)*180/pi); % valor em graus
end

Obs.: Falta pequenas adaptações para transformar FPB2a_ordem.m em algo como FPB4a_ordem.m.

v. Script para calcular impacto do Filtro

Segue código exemplo impacto_FPB.m que computa o impacto causado pelo filtro (executado na rotina anterior FPB2a_ordem.m) sobre os componentes da onda quadrada (calculados no script onda_quadrada_fourier.m). Note que estes 3 script devem ser executados em sequência sem limpar variáveis no ambiente do Matlab (sem usar comando clear entre a execução das mesmas).

xxxxxxxxxx
% impacto_FPB.m
% Gera tabela mostrando impacto causado pelo FPB na onda quadrada
% Executar antes: 'FPB2a_ordem.m'
% Fernando Passold, em 18/06/2022
​
clear amp_orig amp_final y_orig y_filt % evigar problemas se re-executar script
​
disp('Impacto causado pelo FPB sobre a onda Quadrada');
disp(' ');
u=length(freq); % elementos presentes dentro vetor freq
disp('| Freq (Hz) | Amplitude Original | Ganho Filtro | Atenuação Filtro | Amplitude Final | Defasagem |');
disp('|   ---:    |       ---:         |   ---:       |    ---:          |    ---:         |   ---:    |'); 
for k=1:u  % varre freq's desejadas
    fprintf('| %g |', freq(k));
    harmonica(k) = 2*k-1; % determina numero da harmonica
    amp_orig(k) = 1/harmonica(k);
    fprintf(' %g |', amp_orig(k));
    fprintf(' %g |', Mag(k)); % "ganho" do filtro
    fprintf(' %g dB |', 20*log10(Mag(k))); % impacto do filtro em dB
    amp_final(k) = amp_orig(k)*Mag(k);
    fprintf(' %g |', amp_final(k));
    fprintf(' %gº |\n', Phase(k)*180/pi); % valor em graus
end
disp(' ');
​
% Gera gráfico temporal comparando onda quadrada original x filtrada
% Parte do código baseado em 'onda_quadrada_fourier.m'
​
fs=f*50*20; % freq. "amostragem" onda quadrada (p/efeitos síntese gráficos)
TT=1/fs;
ciclos=2*T; % número de ciclos plotados da onda quadrada
​
t=0:TT:ciclos; % forma vetor tempo
t_leng=length(t); % numero de pontos
for tt=1:t_leng   % varrendo vetor tempo
    sum_orig = 0;
    sum_filt = 0;
    for k=1:u  % varre as freq's das harmonicas
        % freq(h) = frequencia da harmonica k
        sum_orig = sum_orig + amp_orig(k)*sin(2*pi*freq(k)*t(tt));
        sum_filt = sum_filt + amp_final(k)*sin(2*pi*freq(k)*t(tt)+Phase(k));
    end
    y_orig(tt)=sum_orig;
    y_filt(tt)=sum_filt;
end
figure;
plot(t,y_orig,'m--', t,y_filt,'b-');
grid
texto=num2str(n);
title(['Onda Quadrada Filtrada']);
xlabel('t (seg)');
ylabel('y(t)');
legend('Onda original','Onda filtrada')
​
% Espectro linear da onda quadrada original x filtrada
figure;
subplot(211);
stem(freq, G, 'm--'); % note que são "impulsos" em freq's ímpares
hold on;
stem(freq, amp_final, 'b-');
title('Espectro Onda Quadrada (Magnitudes)');
xlabel('Frequência (Hz)');
ylabel('Amplitude');
grid
​
subplot(212); % gráfico da Fase
% Acrescentando pontos à esquerda do gráfico numa década inferior
% a da 1a-harmônica da onda quadrada.
clear freq2 Phase2 Ph_original
freq2=[f/10 freq];
Phase2=[0 Phase];
uu=length(freq2);
Ph_original=zeros(1,uu);
plot(freq2, Ph_original*180/pi, 'm--')
hold on
plot(freq2, Phase2*180/pi, 'bo-')
% acrescentando texto com No. da harmônica
for k=1:u
    texto = num2str(harmonica(k));
    text(freq(k)*1.05, 0.95*Phase(k)*180/pi, texto);
end
set(gca, 'XScale', 'log')
title('Fase');
xlabel('Log_{10} Freq (Hz)')
ylabel('Fase (graus)');
​
grid

Além de gráricos, o script anterior gera uma tabela (compatível Markdown) na janela de comandos como mostrado à seguir:

xxxxxxxxxx
Impacto do filtro:
​
| Freq (Hz) | Amplitude Original | Ganho Filtro | Atenuação Filtro | Amplitude Final | Defasagem |
| --------: | -----------------: | -----------: | ---------------: | --------------: | --------: |
|         1 |                  1 |          0.8 |       -1.9382 dB |             0.8 |  53.1301º |
|         3 |           0.333333 |     0.307692 |      -10.2377 dB |        0.102564 |   112.62º |
|         5 |                0.2 |     0.137931 |      -17.2068 dB |       0.0275862 |  136.397º |
|         7 |           0.142857 |    0.0754717 |      -22.4443 dB |       0.0107817 |  148.109º |
|         9 |           0.111111 |    0.0470588 |      -26.5472 dB |      0.00522876 |  154.942º |
|        11 |          0.0909091 |        0.032 |       -29.897 dB |      0.00290909 |   159.39º |
|        13 |          0.0769231 |    0.0231214 |      -32.7197 dB |      0.00177857 |  162.508º |
|        15 |          0.0666667 |    0.0174672 |      -35.1555 dB |      0.00116448 |  164.811º |
|        17 |          0.0588235 |    0.0136519 |      -37.2962 dB |     0.000803052 |   166.58º |
|        19 |          0.0526316 |    0.0109589 |      -39.2047 dB |     0.000576784 |  167.982º |
|        21 |           0.047619 |   0.00898876 |       -40.926 dB |     0.000428036 |  169.119º |
|        23 |          0.0434783 |   0.00750469 |      -42.4933 dB |     0.000326291 |  170.061º |
|        25 |               0.04 |    0.0063593 |      -43.9318 dB |     0.000254372 |  170.852º |
|        27 |           0.037037 |   0.00545703 |      -45.2609 dB |     0.000202112 |  171.527º |
|        29 |          0.0344828 |   0.00473373 |      -46.4959 dB |     0.000163232 |   172.11º |
|        31 |          0.0322581 |   0.00414508 |      -47.6493 dB |     0.000133712 |  172.617º |
|        33 |           0.030303 |   0.00365965 |      -48.7312 dB |     0.000110899 |  173.064º |
|        35 |          0.0285714 |   0.00325468 |      -49.7498 dB |     9.29908e-05 |  173.459º |
|        37 |           0.027027 |   0.00291333 |      -50.7122 dB |     7.87386e-05 |  173.812º |
|        39 |           0.025641 |   0.00262295 |      -51.6242 dB |     6.72551e-05 |  174.129º |
|        41 |          0.0243902 |   0.00237389 |      -52.4908 dB |     5.78997e-05 |  174.415º |
|        43 |          0.0232558 |   0.00215866 |      -53.3163 dB |     5.02014e-05 |  174.674º |
|        45 |          0.0222222 |   0.00197141 |      -54.1044 dB |     4.38092e-05 |   174.91º |
|        47 |          0.0212766 |    0.0018075 |      -54.8584 dB |     3.84575e-05 |  175.127º |
|        49 |          0.0204082 |    0.0016632 |      -55.5811 dB |     3.39429e-05 |  175.325º |
|        51 |          0.0196078 |   0.00153551 |       -56.275 dB |      3.0108e-05 |  175.509º |
|        53 |          0.0188679 |   0.00142197 |      -56.9422 dB |     2.68296e-05 |  175.678º |
|        55 |          0.0181818 |   0.00132057 |      -57.5848 dB |     2.40103e-05 |  175.835º |
|        57 |          0.0175439 |   0.00122963 |      -58.2045 dB |     2.15725e-05 |  175.981º |
|        59 |          0.0169492 |   0.00114778 |      -58.8029 dB |     1.94538e-05 |  176.117º |
|        61 |          0.0163934 |   0.00107383 |      -59.3813 dB |     1.76037e-05 |  176.244º |
|        63 |           0.015873 |    0.0010068 |      -59.9412 dB |     1.59809e-05 |  176.363º |
|        65 |          0.0153846 |   0.00094585 |      -60.4836 dB |     1.45515e-05 |  176.475º |
|        67 |          0.0149254 |  0.000890274 |      -61.0095 dB |     1.32877e-05 |   176.58º |
|        69 |          0.0144928 |  0.000839454 |      -61.5201 dB |      1.2166e-05 |  176.679º |
|        71 |          0.0140845 |  0.000792864 |       -62.016 dB |     1.11671e-05 |  176.773º |
|        73 |          0.0136986 |  0.000750047 |      -62.4982 dB |     1.02746e-05 |  176.861º |
|        75 |          0.0133333 |  0.000710606 |      -62.9674 dB |     9.47474e-06 |  176.945º |
|        77 |           0.012987 |  0.000674195 |      -63.4243 dB |     8.75578e-06 |  177.024º |

Fernando Passold @ 2025/1