Aproximação de Padé

Intro

A aproximação de Padé é uma técnica utilizada para aproximar funções de transferência não racionais (como atrasos puros) por funções racionais, facilitando a análise e projeto de controladores.

A aproximação criada por Henri Padé, por volta de 1890, é obtida através de uma expansão em série de Taylor da função exponencial $e^{-sT}$, combinada com uma função racional que a aproxima. Vamos deduzir as aproximações de 1ª e 2ª ordens passo a passo.

1. Aproximação de Padé de 1ª Ordem para $e^{-sT}$

Queremos aproximar $e^{-sT}$ por uma função racional da forma:

$R(s) = \dfrac{1 + a s}{1 + b s}$

Passos para a Dedução:

1. Expansão em Série de Taylor de $e^{-sT}$: $e^{-sT} \approx 1 - sT + \dfrac{(sT)^2}{2} - \dfrac{(sT)^3}{6} + \cdots$ (Para aproximação de 1ª ordem, consideramos até o termo linear.)

2. Expansão em Série de Taylor de $R(s)$: $R(s) = \dfrac{1 + a s}{1 + b s} \approx (1 + a s)(1 - b s + b^2 s^2 - \cdots) \approx 1 + (a - b)s + \mathcal{O}(s^2)$

3. Igualando os coeficientes com a expansão de $e^{-sT}$: $1 - sT \approx 1 + (a - b)s$ Portanto: $a - b = -T$

4. Escolha de $a$ e $b$ (critério de Padé):

   • Padé de 1ª ordem usa $a = -T/2$ e $b = T/2$, pois isso garante que o erro seja minimizado em torno de $s = 0$.

5. Resultado final: $e^{-sT} \approx \dfrac{1 - \dfrac{T}{2} s}{1 + \dfrac{T}{2} s}$ Supondo que o atraso fosse de 2 segundos, $T = 2$: $e^{-2s} \approx \dfrac{1 - s}{1 + s}$

2. Aproximação de Padé de 2ª Ordem para $e^{-sT}$

Agora, aproximamos $e^{-sT}$ por uma função racional quadrática:

$R(s) = \dfrac{1 + a s + b s^2}{1 + c s + d s^2}$

Passos para a Dedução

1. Expansão em Série de Taylor de $e^{-sT}$ (até 2ª ordem): $e^{-sT} \approx 1 - sT + \dfrac{(sT)^2}{2} - \dfrac{(sT)^3}{6} + \cdots$

2. Expansão em Série de Taylor de $R(s)$: $R(s) \approx 1 + (a - c)s + \left(b - a c + c^2 - d\right)s^2 + \mathcal{O}(s^3)$

3. Igualando os coeficientes com $e^{-sT}$: $1 - T s + \dfrac{T^2}{2} s^2 \approx 1 + (a - c)s + \left(b - a c + c^2 - d\right)s^2$ Obtemos o sistema: $\begin{cases} a - c = -T \\ b - a c + c^2 - d = \dfrac{T^2}{2} \end{cases}$

4. Critério de Padé (simetria e minimização do erro):

   • Escolha $a = -c$ (simetria).
   • Resolvendo, obtém-se: $a = -\dfrac{T}{2}, \quad c = \dfrac{T}{2}, \quad b = \dfrac{T^2}{12}, \quad d = \dfrac{T^2}{12}$

5. Resultado final: $e^{-sT} \approx \dfrac{1 - \dfrac{T}{2} s + \dfrac{T^2}{12} s^2}{1 + \dfrac{T}{2} s + \dfrac{T^2}{12} s^2}$ Supondo que o atraso fosse de 2 segundos, $T = 2$: $e^{-2s} \approx \dfrac{1 - s + \dfrac{s^2}{3}}{1 + s + \dfrac{s^2}{3}}$

Resumo das Fórmulas Gerais

Observações:

• Quanto maior a ordem, melhor a aproximação, mas mais complexa a função.
• A 1ª ordem introduz um zero no semiplano direito (comportamento não mínimo de fase).
• A 2ª ordem captura melhor o atraso, mas ainda tem algum erro em altas frequências.

Exemplo:

Como seria usada a aproximação de Padé para considerar um atraso de transporte de uns 2 segundos num sistema de primeira ordem com constante de tempo de 1 minuto? Considere mostrar equações e eventualmente realizar simulações usando Matlab.

Aproximação de Padé para um Atraso de Transporte

Um atraso puro $e^{-sT}$ pode ser aproximado por uma função racional usando Padé. Para um atraso de $T = 2$ segundos, a aproximação de Padé de 1ª ordem é:

$e^{-2s} \approx \dfrac{1 - s}{1 + s}$

E a de 2ª ordem (mais precisa):

$e^{-2s} \approx \dfrac{1 - s + \dfrac{s^2}{3}}{1 + s + \dfrac{s^2}{3}}$

Sistema de 1ª Ordem com Atraso

Considere um sistema de primeira ordem com constante de tempo $\tau = 1$ minuto (60 segundos) e ganho estático $K = 1$:

$G(s) = \dfrac{1}{60s + 1} \cdot e^{-2s}$

Substituindo o atraso pela aproximação de Padé de 1ª ordem:

$G_{approx}(s) = \dfrac{1}{60s + 1} \cdot \dfrac{1 - s}{1 + s}$

Simulação no MATLAB

Podemos comparar a resposta ao degrau do sistema exato (usando a função pade() no MATLAB) e da aproximação:

xxxxxxxxxx
% Sistema original com atraso
s = tf('s');
G = 1 / (60*s + 1) * exp(-2*s);
​
% Aproximação de Padé de 1ª ordem
[num_pade, den_pade] = pade(2, 1);  % Atraso de 2s, ordem 1
Pade1 = tf(num_pade, den_pade);
G_approx1 = 1 / (60*s + 1) * Pade1;
​
% Aproximação de Padé de 2ª ordem
[num_pade2, den_pade2] = pade(2, 2);  % Atraso de 2s, ordem 2
Pade2 = tf(num_pade2, den_pade2);
G_approx2 = 1 / (60*s + 1) * Pade2;
​
% Simulação da resposta ao degrau
figure;
step(G, 'r--', G_approx1, 'b', G_approx2, 'g--');
legend('Exato (com atraso)', 'Padé 1ª Ordem', 'Padé 2ª Ordem');
grid on;

Resultados Esperados

• A aproximação de 1ª ordem introduz um zero no semiplano direito (comportamento não mínimo de fase), causando um "mergulho" inicial na resposta.
• A aproximação de 2ª ordem é mais precisa e suaviza esse efeito.
• Quanto maior a ordem de Padé, melhor a aproximação, mas maior a complexidade do modelo.

Resultados obtidos

Resposta ao degrau para os 3 sistemas:

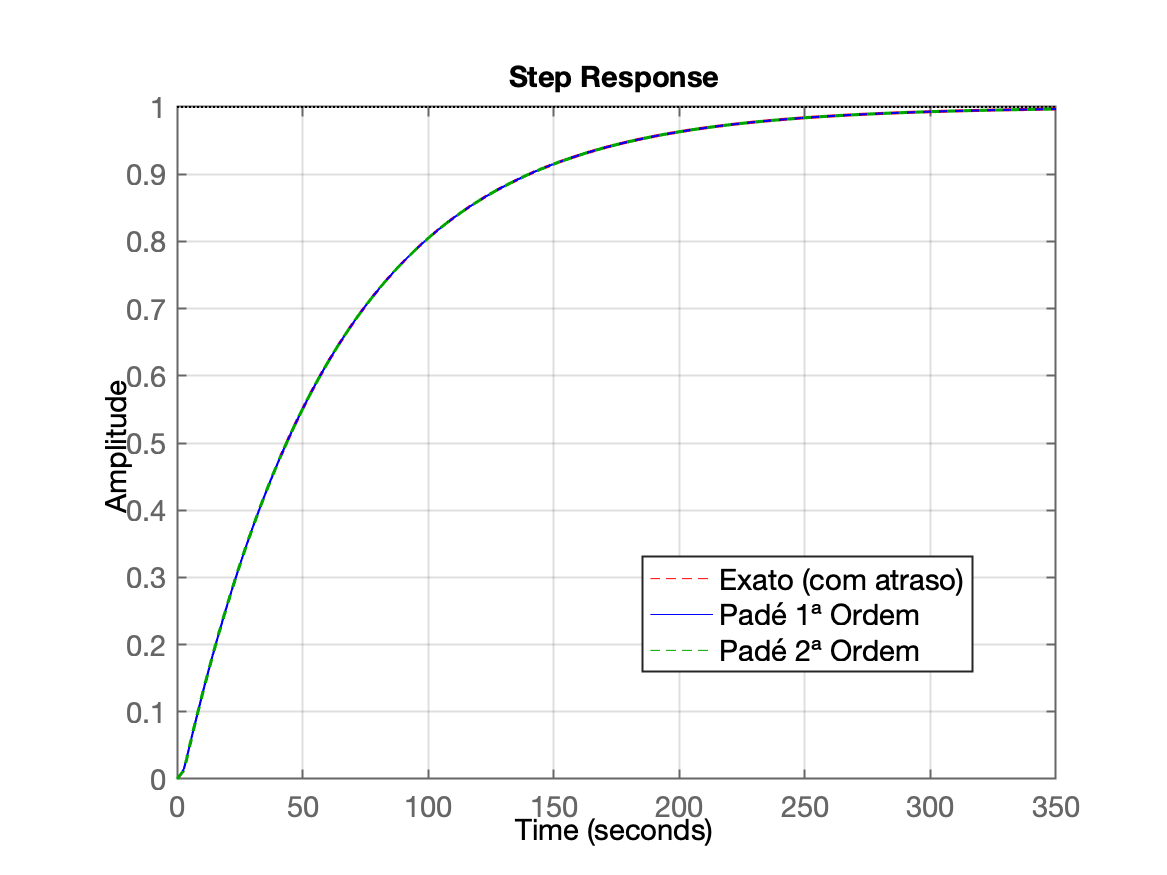
Primeiros 10 segundos	Intervalo final
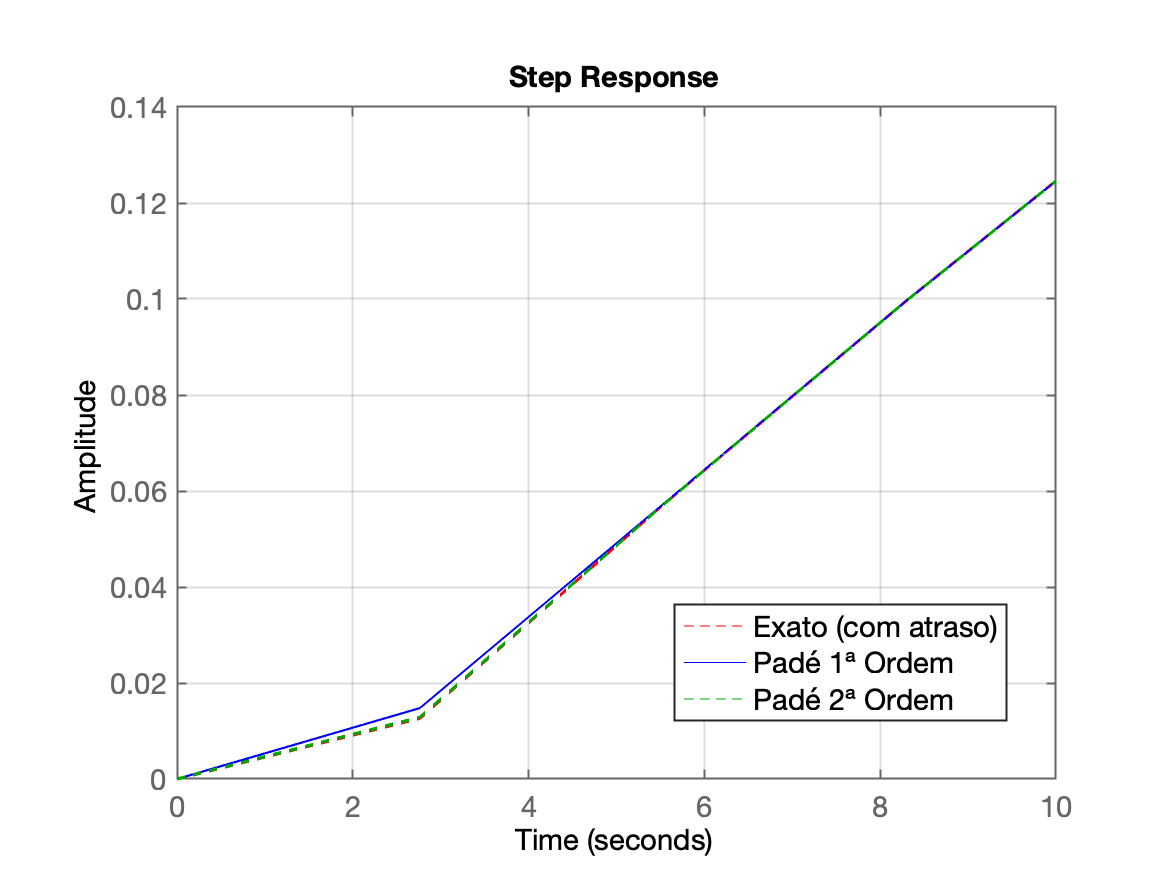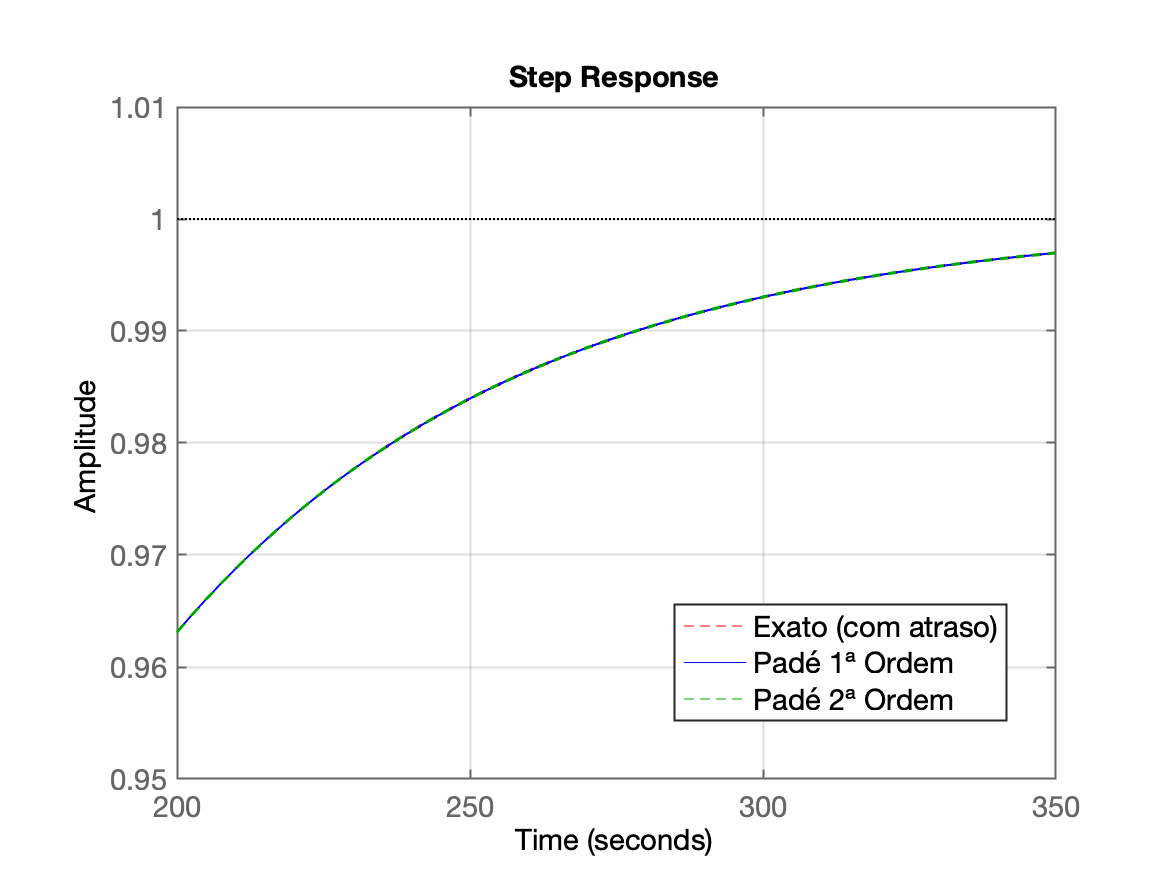xlim([0 10])	axis([200 350 0.95 1.01])

Note:

>> zpk(G) % função transferência do sistema com o atraso
 
               0.016667
  exp(-2*s) * -----------
              (s+0.01667)
 
Continuous-time zero/pole/gain model.
​
>> % Podemos incluir uma função similar sem o atraso:
>> Gr=tf(1, [60 1]);
>> zpk(Gr)
​
ans =
 
   0.016667
  -----------
  (s+0.01667)
 
Continuous-time zero/pole/gain model.
​
>> zpk(Pade1)
 
  - (s-1)
  -------
   (s+1)
 
Continuous-time zero/pole/gain model.
​
>> zpk(Pade2)
 
  (s^2 - 3s + 3)
  --------------
  (s^2 + 3s + 3)
 
Continuous-time zero/pole/gain model.
​
>> % Observando as tf's das funções aproximadas:
>> zpk(G_approx1)   % aproximação Pade de 1a-ordem
 
   -0.016667 (s-1)
  -----------------
  (s+1) (s+0.01667)
 
Continuous-time zero/pole/gain model.
​
>> zpk(G_approx2)   % aproximação Pade de 2a-ordem
 
   0.016667 (s^2 - 3s + 3)
  --------------------------
  (s+0.01667) (s^2 + 3s + 3)
 
Continuous-time zero/pole/gain model.
​
>> 

Mas mais interessante é perceber o RL e corresponde resposta temporal ao degrau:

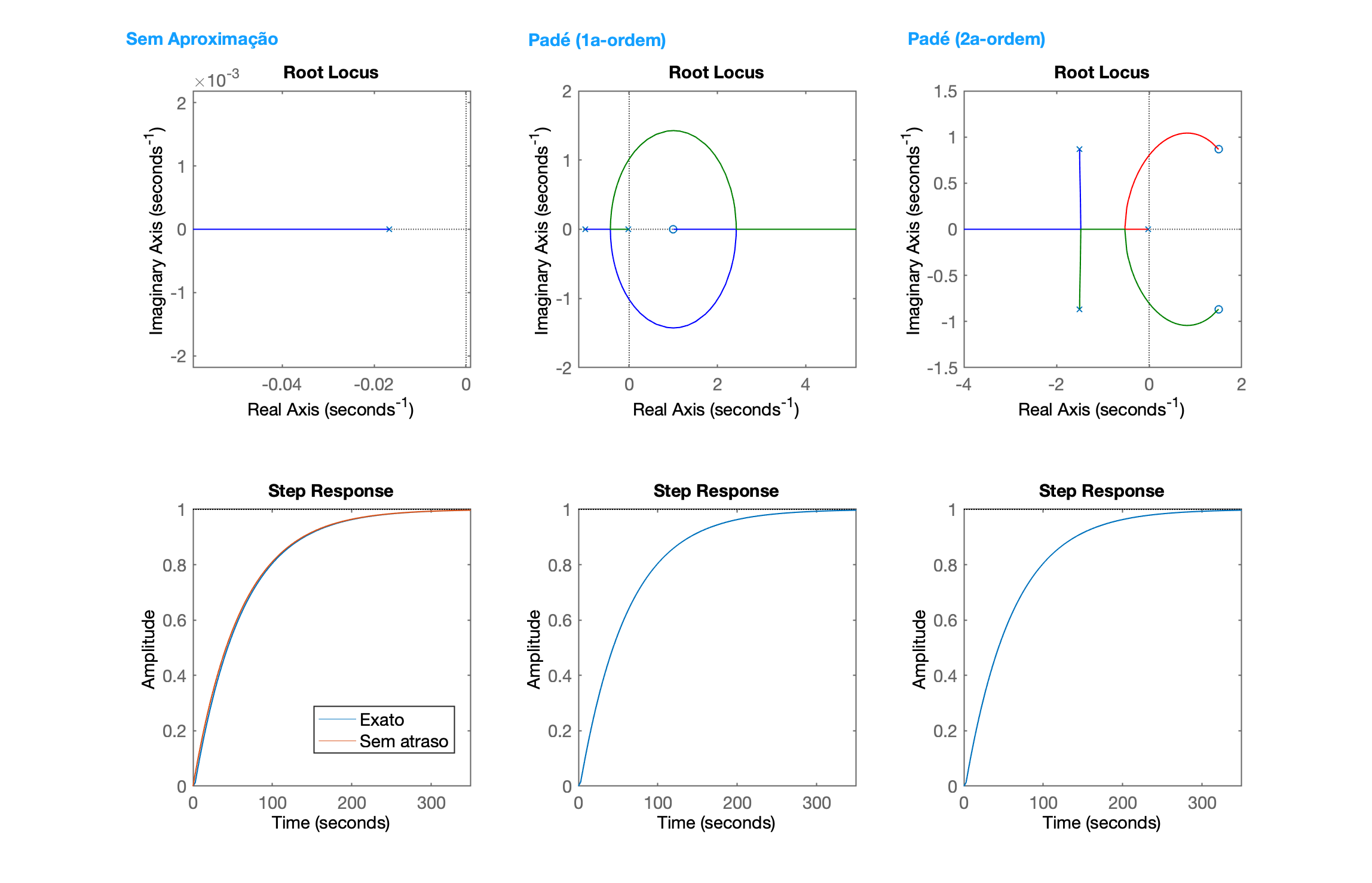
x
>> % Gráfico comparativo
>> subplot(2,3,1) % 2 linhas, 3 colunas, 1a-célula:
>> rlocus(Gr)
>> subplot(2,3,4)
>> step(G, Gr)
>> legend('Com atraso', 'Sem atraso')
>> subplot(2,3,2)
>> rlocus(G_approx1)
>> subplot(2,3,5)
>> step(G_approx1)
>> subplot(2,3,3)
>> rlocus(G_approx2)
>> subplot(2,3,6)
>> step(G_approx2)
>> subplot(2,3,4)
>> xlim([0 350])
>> step(G,Gr)
>> axis([0 350 0 1])
>> legend('Exato', 'Sem atraso')

Conclusão

A aproximação de Padé permite substituir o atraso por uma função racional, facilitando análises no domínio da frequência e projeto de controladores. No entanto, ordens baixas podem introduzir distorções, então deve-se escolher a ordem adequada conforme a precisão desejada.

Resumo

Fico feliz que tenha gostado da explicação! A aproximação de Padé é uma ferramenta poderosa para lidar com atrasos em sistemas de controle, e entender sua dedução ajuda muito na aplicação prática.

Recapitulando

1. Padé de 1ª ordem:

   • Aproxima $e^{-sT}$ como $\dfrac{1 - \dfrac{T}{2}s}{1 + \dfrac{T}{2}s}$.
   • Simples, mas introduz um zero no semiplano direito (resposta inicial "inversa", sistema de fase não mínima).

2. Padé de 2ª ordem:

   • Aproxima $e^{-sT}$ como $\dfrac{1 - \dfrac{T}{2}s + \dfrac{T^2}{12}s^2}{1 + \dfrac{T}{2}s + \dfrac{T^2}{12}s^2}$.
   • Mais precisa, especialmente para atrasos maiores.

Se quiser explorar mais

• Podemos comparar ordens superiores (3ª, 4ª...) para ver como a aproximação melhora.
• Podemos analisar o erro de fase em diferentes frequências.
• Podemos aplicar isso em projeto de controladores (como PID com compensação de atraso).
• Wikipedia: Padé approximant.

Fernando Passold, em 15/05/2025